|
Proportional Hazards Models
Proportional hazards models are a class of survival models in statistics. Survival models relate the time that passes, before some event occurs, to one or more covariates that may be associated with that quantity of time. In a proportional hazards model, the unique effect of a unit increase in a covariate is multiplicative with respect to the hazard rate. The hazard rate at time t is the probability per short time d''t'' that an event will occur between t and t + dt given that up to time t no event has occurred yet. For example, taking a drug may halve one's hazard rate for a stroke occurring, or, changing the material from which a manufactured component is constructed, may double its hazard rate for failure. Other types of survival models such as accelerated failure time models do not exhibit proportional hazards. The accelerated failure time model describes a situation where the biological or mechanical life history of an event is accelerated (or decelerated). Background ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Survival Analysis
Survival analysis is a branch of statistics for analyzing the expected duration of time until one event occurs, such as death in biological organisms and failure in mechanical systems. This topic is called reliability theory, reliability analysis or reliability engineering in engineering, duration analysis or duration modelling in economics, and event history analysis in sociology. Survival analysis attempts to answer certain questions, such as what is the proportion of a population which will survive past a certain time? Of those that survive, at what rate will they die or fail? Can multiple causes of death or failure be taken into account? How do particular circumstances or characteristics increase or decrease the probability of survival? To answer such questions, it is necessary to define "lifetime". In the case of biological survival, death is unambiguous, but for mechanical reliability, failure may not be well-defined, for there may well be mechanical systems in which failure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
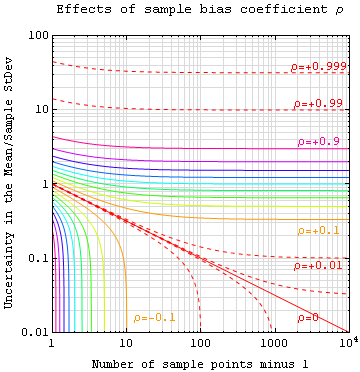
Standard Error
The standard error (SE) of a statistic (usually an estimator of a parameter, like the average or mean) is the standard deviation of its sampling distribution or an estimate of that standard deviation. In other words, it is the standard deviation of statistic values (each value is per sample that is a set of observations made per sampling on the same population). If the statistic is the sample mean, it is called the standard error of the mean (SEM). The standard error is a key ingredient in producing confidence intervals. The sampling distribution of a mean is generated by repeated sampling from the same population and recording the sample mean per sample. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely arou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annals Of Statistics
The ''Annals of Statistics'' is a peer-reviewed statistics journal published by the Institute of Mathematical Statistics. It was started in 1973 as a continuation in part of the '' Annals of Mathematical Statistics (1930)'', which was split into the ''Annals of Statistics'' and the '' Annals of Probability''. The journal CiteScore is 5.8, and its SCImago Journal Rank is 5.877, both from 2020. Articles older than 3 years are available on JSTOR, and all articles since 2004 are freely available on the arXiv arXiv (pronounced as "archive"—the X represents the Chi (letter), Greek letter chi ⟨χ⟩) is an open-access repository of electronic preprints and postprints (known as e-prints) approved for posting after moderation, but not Scholarly pee .... Editorial board The following persons have been editors of the journal: * Ingram Olkin (1972–1973) * I. Richard Savage (1974–1976) * Rupert G. Miller (1977–1979) * David V. Hinkley (1980–1982) * Michael D. Perlm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
L1-norm
In mathematics, the spaces are function spaces defined using a natural generalization of the Norm (mathematics)#p-norm, -norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue , although according to the Nicolas Bourbaki, Bourbaki group they were first introduced by Frigyes Riesz . spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines. Preliminaries The -norm in finite dimensions The Euclidean length of a vector x = (x_1, x_2, \dots, x_n) in the n-dimensional real number, real vector space \Reals^n is given by the Euclidean norm: \, x\, _2 = \left(^2 + ^2 + \dotsb + ^2\right)^. The Euclidean distance between two points x and y is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lasso (statistics)
In statistics and machine learning, lasso (least absolute shrinkage and selection operator; also Lasso, LASSO or L1 regularization) is a regression analysis method that performs both variable selection and Regularization (mathematics), regularization in order to enhance the prediction accuracy and interpretability of the resulting statistical model. The lasso method assumes that the coefficients of the linear model are sparse, meaning that few of them are non-zero. It was originally introduced in geophysics, and later by Robert Tibshirani, who coined the term. Lasso was originally formulated for linear regression models. This simple case reveals a substantial amount about the estimator. These include its relationship to ridge regression and best subset selection and the connections between lasso coefficient estimates and so-called soft thresholding. It also reveals that (like standard linear regression) the coefficient estimates do not need to be unique if covariates are collinear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Linear Model
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by allowing the magnitude of the variance of each measurement to be a function of its predicted value. Generalized linear models were formulated by John Nelder and Robert Wedderburn as a way of unifying various other statistical models, including linear regression, logistic regression and Poisson regression. They proposed an iteratively reweighted least squares method for maximum likelihood estimation (MLE) of the model parameters. MLE remains popular and is the default method on many statistical computing packages. Other approaches, including Bayesian regression and least squares fitting to variance stabilized responses, have been developed. Intuition Ordinary linear regression predicts the expected value of a given unknown quanti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Regression
In statistics, Poisson regression is a generalized linear model form of regression analysis used to model count data and contingency tables. Poisson regression assumes the response variable ''Y'' has a Poisson distribution, and assumes the logarithm of its expected value can be modeled by a linear combination of unknown parameters. A Poisson regression model is sometimes known as a log-linear model, especially when used to model contingency tables. Negative binomial regression is a popular generalization of Poisson regression because it loosens the highly restrictive assumption that the variance is equal to the mean made by the Poisson model. The traditional negative binomial regression model is based on the Poisson-gamma mixture distribution. This model is popular because it models the Poisson heterogeneity with a gamma distribution. Poisson regression models are generalized linear models with the logarithm as the (canonical) link function, and the Poisson distribution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics In Medicine (journal)
'' Statistics in Medicine'' is a peer-reviewed statistics journal published by Wiley. Established in 1982, the journal publishes articles on medical statistics. The journal is indexed by ''Mathematical Reviews'' and SCOPUS. According to the ''Journal Citation Reports'', the journal has a 2023 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 1.8. References External links * Medical statistics journals Academic journals established in 1982 English-language journals Wiley (publisher) academic journals {{statistics-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiparametric Model
In statistics, a semiparametric model is a statistical model that has parametric and nonparametric components. A statistical model is a parameterized family of distributions: \ indexed by a parameter \theta. * A parametric model is a model in which the indexing parameter \theta is a vector in k-dimensional Euclidean space, for some nonnegative integer k.. Thus, \theta is finite-dimensional, and \Theta \subseteq \mathbb^k. * With a nonparametric model, the set of possible values of the parameter \theta is a subset of some space V, which is not necessarily finite-dimensional. For example, we might consider the set of all distributions with mean 0. Such spaces are vector spaces with topological structure, but may not be finite-dimensional as vector spaces. Thus, \Theta \subseteq V for some possibly infinite-dimensional space V. * With a semiparametric model, the parameter has both a finite-dimensional component and an infinite-dimensional component (often a real-valued funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weibull Distribution
In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page. The distribution is named after Swedish mathematician Waloddi Weibull, who described it in detail in 1939, although it was first identified by René Maurice Fréchet and first applied by to describe a Particle-size distribution, particle size distribution. Definition Standard parameterization The probability density function of a Weibull random variable is : f(x;\lambda,k) = \begin \frac\left(\frac\right)^e^, & x\geq0 ,\\ 0, & x 0 is the ''shape parameter'' and λ > 0 is the ''scale parameter'' of the distribution. Its Cumulative distribution function#Complementary cumulative distribution function (tail distribution), complementary cumulative distribution function is a stretch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The method is widely used in areas such as regression analysis, curve fitting and data modeling. The least squares method can be categorized into linear and nonlinear forms, depending on the relationship between the model parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. History Founding The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Additive Hazards Model
Additive may refer to: Mathematics * Additive function, a function in number theory * Additive map, a function that preserves the addition operation * Additive set-function see Sigma additivity * Additive category, a preadditive category with finite biproducts * Additive inverse, an arithmetic concept * Additive prime, a prime number where the sum of its digits is a number which is also a prime number. Science * Additive color, as opposed to subtractive color * Additive model, a statistical regression model * Additive synthesis, an audio synthesis technique * Additive genetic effects * Additive quantity, a physical quantity that is additive for subsystems; see Intensive and extensive properties Engineering * Feed additive * Gasoline additive, a substance used to improve the performance of a fuel, lower emissions or clean the engine * Oil additive, a substance used to improve the performance of a lubricant * Weakly additive, the quality of preferences in some logistics problems * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |