|
Product Form Stationary Distribution
In probability theory, a product-form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components. Using capital Pi notation a product-form solution has algebraic form :\text(x_1,x_2,x_3,\ldots,x_n) = B \prod_^n \text(x_i) where ''B'' is some constant. Solutions of this form are of interest as they are computationally inexpensive to evaluate for large values of ''n''. Such solutions in queueing networks are important for finding performance metrics in models of multiprogrammed and time-shared computer systems. Equilibrium distributions The first product-form solutions were found for equilibrium distributions of Markov chains. Trivially, models composed of two or more independent sub-components exhibit a product-form solution by the definition of independence. Initially the term was used in que ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annals Of Applied Probability
'' The Annals of Applied Probability'' is a leading peer review, peer-reviewed mathematics journal published by the Institute of Mathematical Statistics, which is the main international society for researchers in probability and statistics. The journal was established in 1991 by founding editor J. Michael Steele and is indexed by ''Mathematical Reviews'' and Zentralblatt MATH. Its 2009 Mathematical Citation Quotient, MCQ was 1.02. Its impact factor (measured by JCR/ISI-Thomson) evolved from 1.454 in 2014 to 1.786 in 2017. The journal CiteScore is 3.2 and its SCImago Journal Rank is 1.878, both from 2020. It is currently ranked 9th in the field of Probability & Statistics with Applications according to Google Scholar. References External links * Probability journals Academic journals established in 1991 English-language journals Bimonthly journals Institute of Mathematical Statistics academic journals 1991 establishments in the United States {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jackson Network
In queueing theory, a discipline within the mathematical theory of probability, a Jackson network (sometimes Jacksonian network) is a class of queueing network where the equilibrium distribution is particularly simple to compute as the network has a product-form solution. It was the first significant development in the theory of networks of queues, and generalising and applying the ideas of the theorem to search for similar product-form solutions in other networks has been the subject of much research, including ideas used in the development of the Internet. The networks were first identified by James R. Jackson A version from January 1963 is available at http://www.dtic.mil/dtic/tr/fulltext/u2/296776.pdf and his paper was re-printed in the journal ''Management Science’s'' ‘Ten Most Influential Titles of Management Sciences First Fifty Years.’ Jackson was inspired by the work of Burke and Reich, though Jean Walrand notes "product-form results … rea much less immediate re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M/M/1 Queue
In queueing theory, a discipline within the mathematical probability theory, theory of probability, an M/M/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times have an exponential distribution. The model name is written in Kendall's notation. The model is the most elementary of queueing models and an attractive object of study as closed-form expressions can be obtained for many metrics of interest in this model. An extension of this model with more than one server is the M/M/c queue. Model definition An M/M/1 queue is a stochastic process whose state space is the set where the value corresponds to the number of customers in the system, including any currently in service. * Arrivals occur at rate λ according to a Poisson process and move the process from state ''i'' to ''i'' + 1. * Service times have an exponential distribution with rate parameter μ in the M/M/1 queue, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Reaction Network
Chemical reaction network theory is an area of applied mathematics that attempts to model the behaviour of real-world chemical systems. Since its foundation in the 1960s, it has attracted a growing research community, mainly due to its applications in biochemistry and theoretical chemistry. It has also attracted interest from pure mathematicians due to the interesting problems that arise from the mathematical structures involved. History Dynamical properties of reaction networks were studied in chemistry and physics after the invention of the law of mass action. The essential steps in this study were introduction of detailed balance for the complex chemical reactions by Rudolf Wegscheider (1901), development of the quantitative theory of chemical chain reactions by Nikolay Semyonov (1934), development of kinetics of catalytic reactions by Cyril Norman Hinshelwood, and many other results. Three eras of chemical dynamics can be revealed in the flux of research and publications. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martin Feinberg
Martin Feinberg is an American chemical engineer and mathematician known for his work in chemical reaction network theory. Life Born in New York, Feinberg received his undergraduate degree in chemical engineering from The Cooper Union for the Advancement of Science and Art in 1962. A year later, he obtained his master's degree from Purdue University. In 1968, he received his PhD degree from Princeton University. The subject of the doctoral thesis is fluid mechanics and the advisor is William Schowalter. After completing the PhD, he went to work at the University of Rochester, Rochester, NY, where he was a professor of chemical engineering until 1997. He then moved to The Ohio State University, where he serves as Richard M. Morrow Professor of Chemical Engineering and professor of mathematics. Feinberg was a member of the editorial board of the Archive for Rational Mechanics and Analysis from 1978–1991. Research Together with F. J. M. Horn and Roy Jackson, Feinberg created c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
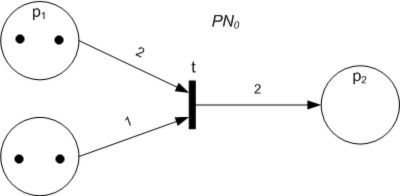
Petri Nets
A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements: places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic
Stochastic (; ) is the property of being well-described by a random probability distribution. ''Stochasticity'' and ''randomness'' are technically distinct concepts: the former refers to a modeling approach, while the latter describes phenomena; in everyday conversation, however, these terms are often used interchangeably. In probability theory, the formal concept of a '' stochastic process'' is also referred to as a ''random process''. Stochasticity is used in many different fields, including image processing, signal processing, computer science, information theory, telecommunications, chemistry, ecology, neuroscience, physics, and cryptography. It is also used in finance (e.g., stochastic oscillator), due to seemingly random changes in the different markets within the financial sector and in medicine, linguistics, music, media, colour theory, botany, manufacturing and geomorphology. Etymology The word ''stochastic'' in English was originally used as an adjective with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PEPA
Performance Evaluation Process Algebra (PEPA) is a stochastic process algebra designed for modelling computer and communication systems introduced by Jane Hillston in the 1990s. The language extends classical process algebras such as Milner's CCS and Hoare's CSP by introducing probabilistic branching and timing of transitions. Rates are drawn from the exponential distribution and PEPA models are finite-state and so give rise to a stochastic process In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables in a probability space, where the index of the family often has the interpretation of time. Sto ..., specifically a continuous-time Markov process (CTMC). Thus the language can be used to study quantitative properties of models of computer and communication systems such as throughput, utilisation and Response time (technology), response time as well as qualitative properties such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
RCAT
In probability theory, the reversed compound agent theorem (RCAT) is a set of sufficient conditions for a stochastic process expressed in any formalism to have a product form stationary distribution (assuming that the process is stationary). The theorem shows that product form solutions in Jackson's theorem, the BCMP theorem and G-networks are based on the same fundamental mechanisms. The theorem identifies a reversed process using Kelly's lemma In probability theory, Kelly's lemma states that for a stationary continuous-time Markov chain A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will change state according to an expon ..., from which the stationary distribution can be computed. Notes Further reading * A short introduction to RCAT. Theorems in probability theory {{Probability-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ruth J
Ruth (or its variants) may refer to: Places France * Château de Ruthie, castle in the commune of Aussurucq in the Pyrénées-Atlantiques département of France Switzerland * Ruth, a hamlet in Cologny United States * Ruth, Alabama * Ruth, Arkansas * Ruth, California * Ruth, Louisiana * Ruth, Kentucky * Ruth, Michigan * Ruth, Mississippi * Ruth, Nevada * Ruth, North Carolina * Ruth, Virginia * Ruth, Washington * Ruth, West Virginia In space * Ruth (lunar crater), crater on the Moon * Ruth (Venusian crater), crater on Venus * 798 Ruth, asteroid People * Ruth (biblical figure) * Ruth (given name) contains list of namesakes including fictional * Princess Ruth or Keʻelikōlani, (1826–1883), Hawaiian princess Surname * A. S. Ruth, American politician * Babe Ruth (1895–1948), American baseball player * Connie Ruth, American politician * Earl B. Ruth (1916–1989), American politician * Elizabeth Ruth, Canadian novelist * Heidi Ruth (born 1996), American soccer player * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |