|
ProbOnto
ProbOnto is a knowledge base and ontology of probability distributions.Main project website, URL: http://probonto.org ProbOnto 2.5 (released on January 16, 2017) contains over 150 uni- and multivariate distributions and alternative parameterizations, more than 220 relationships and re-parameterization formulas, supporting also the encoding of empirical and univariate mixture distributions. Introduction ProbOnto was initially designed to facilitate the encoding of nonlinear-mixed effect models and their annotation in Pharmacometrics Markup Language (PharmML) developed by DDMoRe, an Innovative Medicines Initiative project. However, ProbOnto, due to its generic structure can be applied in other platforms and modeling tools for encoding and annotation of diverse models applicable to discrete (e.g. count, categorical and time-to-event) and continuous data. Knowledge base The knowledge base stores for each distribution: * Probability density or mass functions and where av ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ProbOnto2
ProbOnto is a knowledge base and ontology of probability distributions.Main project website, URL: http://probonto.org ProbOnto 2.5 (released on January 16, 2017) contains over 150 uni- and multivariate distributions and alternative parameterizations, more than 220 relationships and re-parameterization formulas, supporting also the encoding of empirical and univariate mixture distributions. Introduction ProbOnto was initially designed to facilitate the encoding of nonlinear-mixed effect models and their annotation in Pharmacometrics Markup Language (PharmML) developed by DDMoRe, an Innovative Medicines Initiative project. However, ProbOnto, due to its generic structure can be applied in other platforms and modeling tools for encoding and annotation of diverse models applicable to discrete (e.g. count, categorical and time-to-event) and continuous data. Knowledge base The knowledge base stores for each distribution: * Probability density or mass functions and where availa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
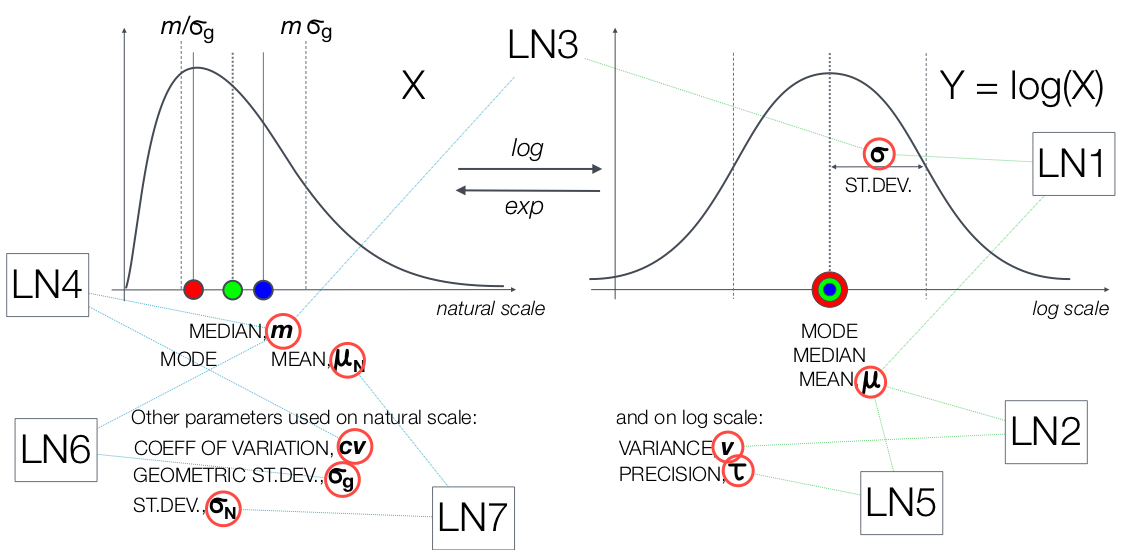
Log-normal Distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable is log-normally distributed, then has a normal distribution. Equivalently, if has a normal distribution, then the exponential function of , , has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. It is a convenient and useful model for measurements in exact and engineering sciences, as well as medicine, economics and other topics (e.g., energies, concentrations, lengths, prices of financial instruments, and other metrics). The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton. The log-normal distribution has also been associated with other names, such as McAlister, Gibrat and Cobb–Douglas. A log-normal process is the statistical realization of the multipl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ontology (information Science)
In computer science and information science, an ontology encompasses a representation, formal naming, and definition of the categories, properties, and relations between the concepts, data, and entities that substantiate one, many, or all domains of discourse. More simply, an ontology is a way of showing the properties of a subject area and how they are related, by defining a set of concepts and categories that represent the subject. Every academic discipline or field creates ontologies to limit complexity and organize data into information and knowledge. Each uses ontological assumptions to frame explicit theories, research and applications. New ontologies may improve problem solving within that domain. Translating research papers within every field is a problem made easier when experts from different countries maintain a controlled vocabulary of jargon between each of their languages. For instance, the definition and ontology of economics is a primary concern in Marxist econo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Survival Function
The survival function is a function that gives the probability that a patient, device, or other object of interest will survive past a certain time. The survival function is also known as the survivor function or reliability function. The term ''reliability function'' is common in engineering while the term ''survival function'' is used in a broader range of applications, including human mortality. The survival function is the complementary cumulative distribution function of the lifetime. Sometimes complementary cumulative distribution functions are called survival functions in general. Definition Let the lifetime ''T'' be a continuous random variable with cumulative distribution function ''F''(''t'') on the interval [0,∞). Its ''survival function'' or ''reliability function'' is: :S(t) = P(\) = \int_t^ f(u)\,du = 1-F(t). Examples of survival functions The graphs below show examples of hypothetical survival functions. The x-axis is time. The y-axis is the proportion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Precision (statistics)
In statistics, the precision matrix or concentration matrix is the matrix inverse of the covariance matrix or dispersion matrix, P = \Sigma^. For univariate distributions, the precision matrix degenerates into a scalar precision, defined as the reciprocal of the variance, p = \frac. Other summary statistics of statistical dispersion also called ''precision'' (or ''imprecision'') include the reciprocal of the standard deviation, p = \frac; the standard deviation itself and the relative standard deviation; as well as the standard error and the confidence interval (or its half-width, the margin of error). Usage One particular use of the precision matrix is in the context of Bayesian analysis of the multivariate normal distribution: for example, Bernardo & Smith prefer to parameterise the multivariate normal distribution in terms of the precision matrix, rather than the covariance matrix, because of certain simplifications that then arise. For instance, if both the prior ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Variance is an important tool in the sciences, where statistical analysis of data is common. The variance is the square of the standard deviation, the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. Standard deviation may be abbreviated SD, and is most commonly represented in mathematical texts and equations by the lower case Greek letter σ (sigma), for the population standard deviation, or the Latin letter '' s'', for the sample standard deviation. The standard deviation of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance. It is algebraically simpler, though in practice less robust, than the average absolute deviation. A useful property of the standard deviation is that, unlike the variance, it is expressed in the same unit as the data. The standard deviation o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set. For a data set, the '' arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the '' sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the '' population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |