|
Polytropic
A polytropic process is a thermodynamic process that obeys the relation: p V^ = C where ''p'' is the pressure, ''V'' is volume, ''n'' is the polytropic index, and ''C'' is a constant. The polytropic process equation describes expansion and compression processes which include heat transfer. Particular cases Some specific values of ''n'' correspond to particular cases: * n=0 for an isobaric process, * n=+\infty for an isochoric process. In addition, when the ideal gas law applies: * n=1 for an isothermal process, * n=\gamma for an isentropic process. Where \gamma is the ratio of the heat capacity at constant pressure (C_P) to heat capacity at constant volume (C_V). Equivalence between the polytropic coefficient and the ratio of energy transfers For an ideal gas in a closed system undergoing a slow process with negligible changes in kinetic and potential energy the process is polytropic, such that p v^ = C where ''C'' is a constant, K = \frac, \gamma = \frac, and with the po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressor
A compressor is a mechanical device that increases the pressure of a gas by reducing its volume. An air compressor is a specific type of gas compressor. Many compressors can be staged, that is, the gas is compressed several times in steps or stages, to increase discharge pressure. Often, the second stage is physically smaller than the primary stage, to accommodate the already compressed gas without reducing its pressure. Each stage further compresses the gas and increases its pressure and also temperature (if inter cooling between stages is not used). Types Compressors are similar to pumps: both increase the pressure on a fluid (such as a gas) and both can transport the fluid through a pipe. The main distinction is that the focus of a compressor is to change the density or volume of the fluid, which is mostly only achievable on gases. Gases are compressible, while liquids are relatively incompressible, so compressors are rarely used for liquids. The main action of a pump is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polytropic
A polytropic process is a thermodynamic process that obeys the relation: p V^ = C where ''p'' is the pressure, ''V'' is volume, ''n'' is the polytropic index, and ''C'' is a constant. The polytropic process equation describes expansion and compression processes which include heat transfer. Particular cases Some specific values of ''n'' correspond to particular cases: * n=0 for an isobaric process, * n=+\infty for an isochoric process. In addition, when the ideal gas law applies: * n=1 for an isothermal process, * n=\gamma for an isentropic process. Where \gamma is the ratio of the heat capacity at constant pressure (C_P) to heat capacity at constant volume (C_V). Equivalence between the polytropic coefficient and the ratio of energy transfers For an ideal gas in a closed system undergoing a slow process with negligible changes in kinetic and potential energy the process is polytropic, such that p v^ = C where ''C'' is a constant, K = \frac, \gamma = \frac, and with the po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Process
Classical thermodynamics considers three main kinds of thermodynamic processes: (1) changes in a system, (2) cycles in a system, and (3) flow processes. (1) A Thermodynamic process is a process in which the thermodynamic state of a system is changed. A change in a system is defined by a passage from an initial to a final state of thermodynamic equilibrium. In classical thermodynamics, the actual course of the process is not the primary concern, and often is ignored. A state of thermodynamic equilibrium endures unchangingly unless it is interrupted by a thermodynamic operation that initiates a thermodynamic process. The equilibrium states are each respectively fully specified by a suitable set of thermodynamic state variables, that depend only on the current state of the system, not on the path taken by the processes that produce the state. In general, during the actual course of a thermodynamic process, the system may pass through physical states which are not describable as th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
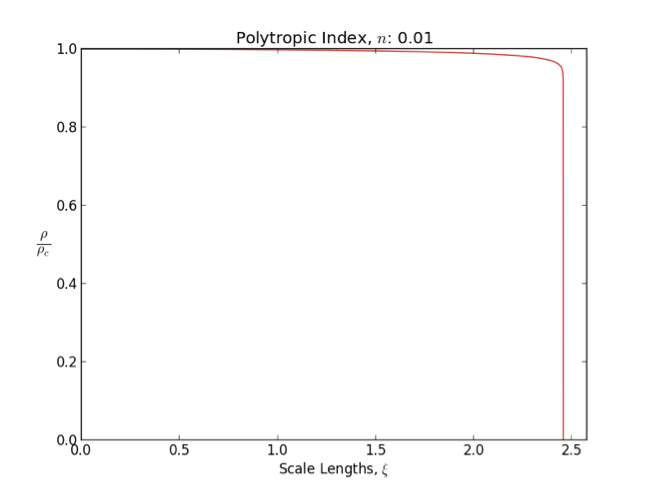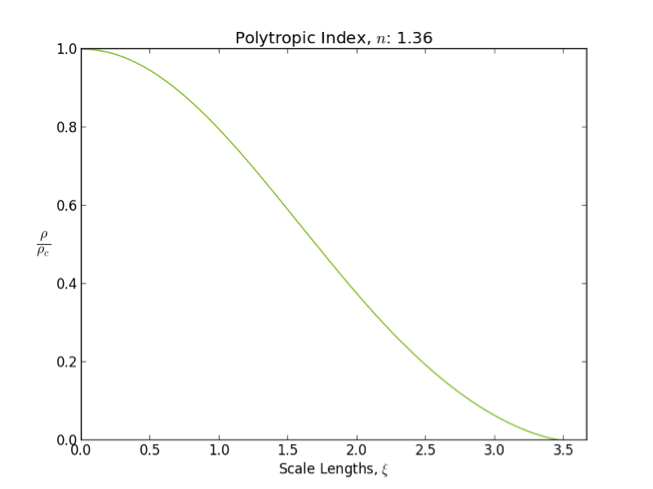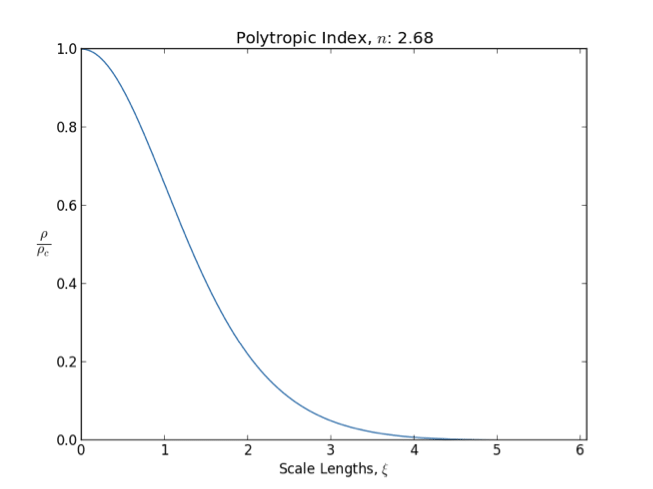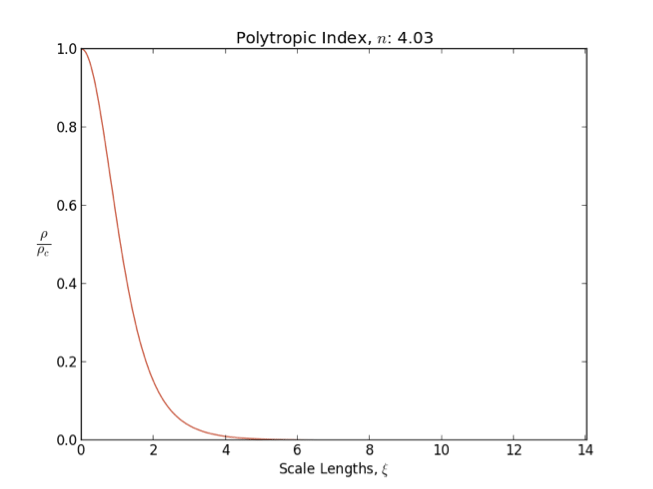
Polytrope
In astrophysics, a polytrope refers to a solution of the Lane–Emden equation in which the pressure depends upon the density in the form P = K \rho^ = K \rho^, where is pressure, is density and is a Constant (mathematics), constant of Proportionality (mathematics), proportionality. The constant is known as the polytropic index; note however that the polytropic index has an alternative definition as with ''n'' as the exponent. This relation need not be interpreted as an equation of state, which states ''P'' as a function of both ρ and ''T'' (the temperature); however in the particular case described by the polytrope equation there are other additional relations between these three quantities, which together determine the equation. Thus, this is simply a relation that expresses an assumption about the change of pressure with radius in terms of the change of density with radius, yielding a solution to the Lane–Emden equation. Sometimes the word ''polytrope'' may refer t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isothermal Process
An isothermal process is a type of thermodynamic process in which the temperature ''T'' of a system remains constant: Δ''T'' = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the system occurs slowly enough to allow the system to be continuously adjusted to the temperature of the reservoir through heat exchange (see quasi-equilibrium). In contrast, an '' adiabatic process'' is where a system exchanges no heat with its surroundings (''Q'' = 0). Simply, we can say that in an isothermal process * T = \text * \Delta T = 0 * dT = 0 * For ideal gases only, internal energy \Delta U = 0 while in adiabatic processes: * Q = 0. Etymology The noun '' isotherm'' is derived from the Ancient Greek words (), meaning "equal", and (), meaning "heat". Examples Isothermal processes can occur in any kind of system that has some means of regulating the temperature, including highly structured machines, and even living ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isothermic Process
An isothermal process is a type of thermodynamic process in which the temperature ''T'' of a system remains constant: Δ''T'' = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the system occurs slowly enough to allow the system to be continuously adjusted to the temperature of the reservoir through heat exchange (see quasi-equilibrium). In contrast, an ''adiabatic process'' is where a system exchanges no heat with its surroundings (''Q'' = 0). Simply, we can say that in an isothermal process * T = \text * \Delta T = 0 * dT = 0 * For ideal gases only, internal energy \Delta U = 0 while in adiabatic processes: * Q = 0. Etymology The noun '' isotherm'' is derived from the Ancient Greek words (), meaning "equal", and (), meaning "heat". Examples Isothermal processes can occur in any kind of system that has some means of regulating the temperature, including highly structured machines, and even living cells ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isentropic Process
An isentropic process is an idealized thermodynamic process that is both Adiabatic process, adiabatic and Reversible process (thermodynamics), reversible. The work (physics), work transfers of the system are friction, frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic (entropy does not change). Thermodynamics, Thermodynamic processes are named based on the effect they would have on the system (ex. isovolumetric: constant volume, isenthalpic: constant enthalpy). Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such. The word "isentropic" derives from the proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and Thermodynamic temperature, temperature respectively; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory of gases, kinetic theory, as was achieved (independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state function, state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isochoric Process
In thermodynamics, an isochoric process, also called a constant-volume process, an isovolumetric process, or an isometric process, is a thermodynamic process during which the volume of the closed system undergoing such a process remains constant. An isochoric process is exemplified by the heating or the cooling of the contents of a sealed, inelastic container: The thermodynamic process is the addition or removal of heat; the isolation of the contents of the container establishes the closed system; and the inability of the container to deform imposes the constant-volume condition. Formalism An isochoric thermodynamic quasi-static process is characterized by constant volume, i.e., .Ansermet, J.-P., Brechet, S.D. (2019). ''Principles of Thermodynamics'', Cambridge University Press, Cambridge UK, p. 113. The process does no pressure-volume work, since such work is defined by W = P \Delta V , where is pressure. The sign convention is such that positive work is performed by the sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isobaric Process
In thermodynamics, an isobaric process is a type of thermodynamic process in which the pressure of the Thermodynamic system, system stays constant: Δ''P'' = 0. The heat transferred to the system does work (thermodynamics), work, but also changes the internal energy (''U'') of the system. This article uses the physics sign convention for work, where positive work is work (thermodynamics)#Sign convention, work done by the system. Using this convention, by the first law of thermodynamics, : Q = \Delta U + W\, where ''W'' is work, ''U'' is internal energy, and ''Q'' is heat. Pressure-volume work by the closed system is defined as: :W = \int \! p \,dV \, where Δ means change over the whole process, whereas ''d'' denotes a differential. Since pressure is constant, this means that : W = p \Delta V\, . Applying the ideal gas law, this becomes : W = n\,R\,\Delta T with ''R'' representing the gas constant, and ''n'' representing the amount of substance, which is ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Process
An adiabatic process (''adiabatic'' ) is a type of thermodynamic process that occurs without transferring heat between the thermodynamic system and its Environment (systems), environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as Work (thermodynamics), work and/or mass flow.. A translation may be founhere. Also a mostly reliabltranslation is to be foundin As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics. The opposite term to "adiabatic" is ''diabatic''. Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient "adiabatic approximation".Bailyn, M. (1994), pp. 52–53. For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of fire, flame temperature by assuming combustion loses no heat to its surroundings. In meteorology, adiabatic expansion an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
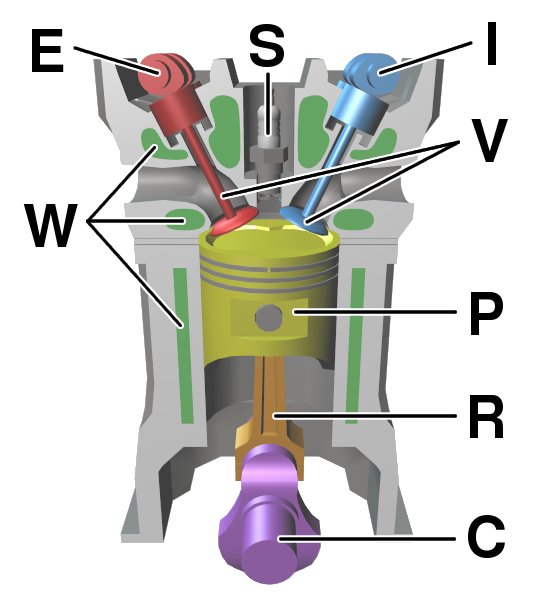
Internal Combustion Engine
An internal combustion engine (ICE or IC engine) is a heat engine in which the combustion of a fuel occurs with an oxidizer (usually air) in a combustion chamber that is an integral part of the working fluid flow circuit. In an internal combustion engine, the expansion of the high-temperature and high-pressure gases produced by combustion applies direct force to some component of the engine. The force is typically applied to pistons (reciprocating engine, piston engine), turbine blades (gas turbine), a Wankel engine, rotor (Wankel engine), or a propulsive nozzle, nozzle (jet engine). This force moves the component over a distance. This process transforms chemical energy into kinetic energy which is used to propel, move or power whatever the engine is attached to. The first commercially successful internal combustion engines were invented in the mid-19th century. The first modern internal combustion engine, the Otto engine, was designed in 1876 by the German engineer Nicolaus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |