|
Phase Offset
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly sca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscillating Sine Wave
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms. Oscillations occur not only in mechanical systems but also in dynamic systems in virtually every area of science: for example the beating of the human heart (for circulation), business cycles in economics, predator–prey population cycles in ecology, geothermal geysers in geology, vibration of strings in guitar and other string instruments, periodic firing of nerve cells in the brain, and the periodic swelling of Cepheid variable stars in astronomy. The term ''vibration'' is precisely used to describe a mechanical oscillation. Oscillation, especially rapid oscillation, may be an undesirable phenomenon in proces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real number, real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as Series (mathematics), infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic function, periodic pheno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longitude
Longitude (, ) is a geographic coordinate that specifies the east- west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians are imaginary semicircular lines running from pole to pole that connect points with the same longitude. The prime meridian defines 0° longitude; by convention the International Reference Meridian for the Earth passes near the Royal Observatory in Greenwich, south-east London on the island of Great Britain. Positive longitudes are east of the prime meridian, and negative ones are west. Because of the Earth's rotation, there is a close connection between longitude and time measurement. Scientifically precise local time varies with longitude: a difference of 15° longitude corresponds to a one-hour difference in local time, due to the differing position in relation to the Sun. Comparing local time to an absol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radio
Radio is the technology of communicating using radio waves. Radio waves are electromagnetic waves of frequency between 3 hertz (Hz) and 300 gigahertz (GHz). They are generated by an electronic device called a transmitter connected to an antenna which radiates the waves. They can be received by other antennas connected to a radio receiver; this is the fundamental principle of radio communication. In addition to communication, radio is used for radar, radio navigation, remote control, remote sensing, and other applications. In radio communication, used in radio and television broadcasting, cell phones, two-way radios, wireless networking, and satellite communication, among numerous other uses, radio waves are used to carry information across space from a transmitter to a receiver, by modulating the radio signal (impressing an information signal on the radio wave by varying some aspect of the wave) in the transmitter. In radar, used to locate and track ob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modulo Operation
In computing and mathematics, the modulo operation returns the remainder or signed remainder of a Division (mathematics), division, after one number is divided by another, the latter being called the ''modular arithmetic, modulus'' of the operation. Given two positive numbers and , modulo (often abbreviated as ) is the remainder of the Euclidean division of by , where is the Division (mathematics), dividend and is the divisor. For example, the expression "5 mod 2" evaluates to 1, because 5 divided by 2 has a quotient of 2 and a remainder of 1, while "9 mod 3" would evaluate to 0, because 9 divided by 3 has a quotient of 3 and a remainder of 0. Although typically performed with and both being integers, many computing systems now allow other types of numeric operands. The range of values for an integer modulo operation of is 0 to . mod 1 is always 0. When exactly one of or is negative, the basic definition breaks down, and programming languages differ in how these valu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beat (acoustics)
In acoustics, a beat is an interference pattern between two sounds of slightly different frequencies, ''perceived'' as a periodic variation in volume whose rate is the difference of the two frequencies. With tuning instruments that can produce sustained tones, beats can be readily recognized. Tuning two tones to a unison will present a peculiar effect: when the two tones are close in pitch but not identical, the difference in frequency generates the beating. The volume varies as in a tremolo as the sounds alternately interfere constructively and destructively. As the two tones gradually approach unison, the beating slows down and may become so slow as to be imperceptible. As the two tones get further apart, their beat frequency starts to approach the range of human pitch perception, the beating starts to sound like a note, and a combination tone is produced. Mathematics and physics of beat tones This phenomenon is best known in acoustics or music, though it can be found in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
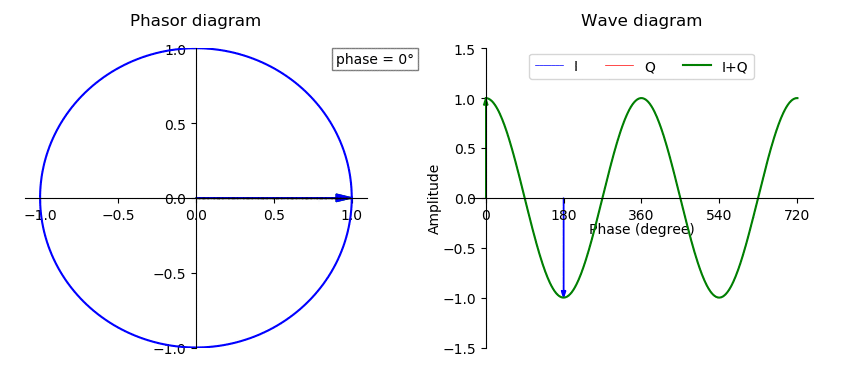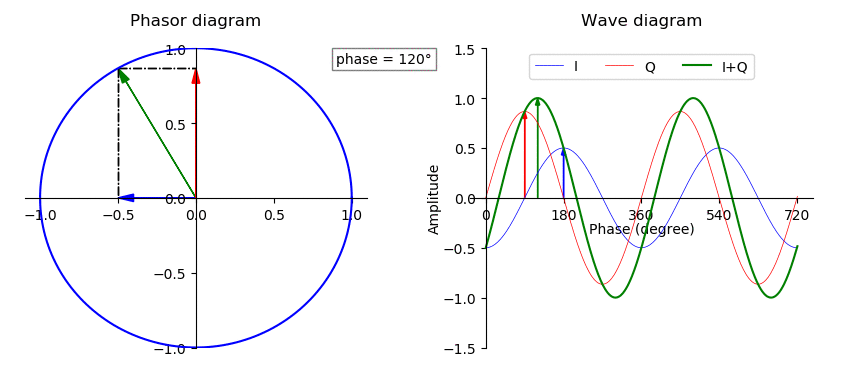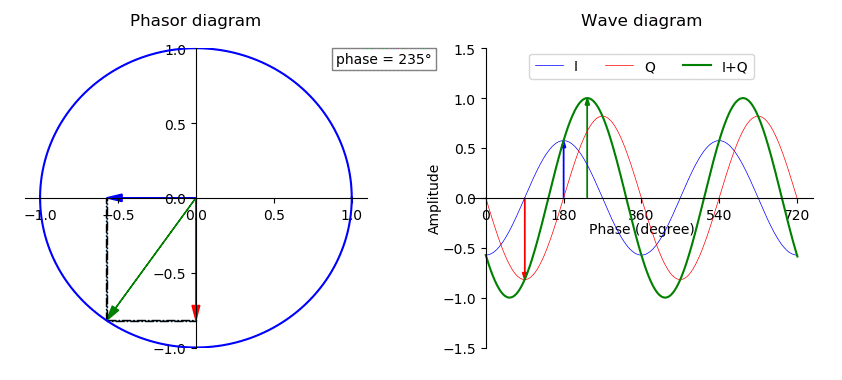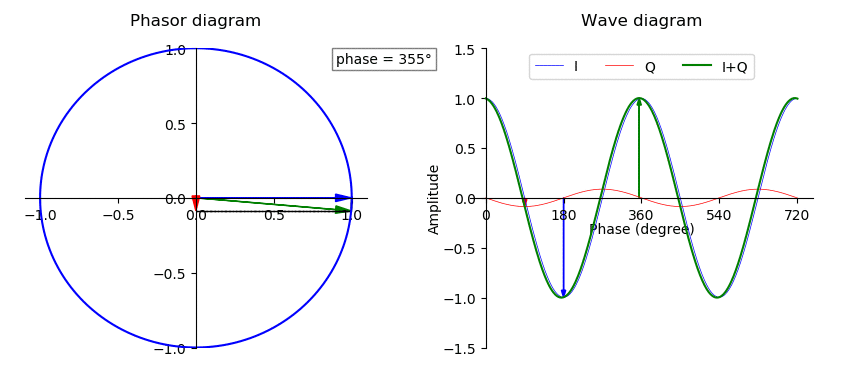
In-phase And Quadrature Components
A sinusoid with modulation can be decomposed into, or synthesized from, two amplitude-modulated sinusoids that are in quadrature phase, i.e., with a phase offset of one-quarter cycle (90 degrees or /2 radians). All three sinusoids have the same center frequency. The two amplitude-modulated sinusoids are known as the in-phase (I) and quadrature (Q) components, which describes their relationships with the amplitude- and phase-modulated carrier. Or in other words, it is possible to create an arbitrarily phase-shifted sine wave, by mixing together two sine waves that are 90° out of phase in different proportions. The implication is that the modulations in some signal can be treated separately from the carrier wave of the signal. This has extensive use in many radio and signal processing applications. I/Q data is used to represent the modulations of some carrier, independent of that carrier's frequency. Orthogonality In vector analysis, a vector with polar coordinates and Car ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interference (wave Propagation)
In physics, interference is a phenomenon in which two coherent waves are combined by adding their intensities or displacements with due consideration for their phase difference. The resultant wave may have greater amplitude (constructive interference) or lower amplitude (destructive interference) if the two waves are in phase or out of phase, respectively. Interference effects can be observed with all types of waves, for example, light, radio, acoustic, surface water waves, gravity waves, or matter waves as well as in loudspeakers as electrical waves. Etymology The word ''interference'' is derived from the Latin words ''inter'' which means "between" and ''fere'' which means "hit or strike", and was used in the context of wave superposition by Thomas Young in 1801. Mechanisms The principle of superposition of waves states that when two or more propagating waves of the same type are incident on the same point, the resultant amplitude at that point is equal to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superposition Principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input ''A'' produces response ''X'', and input ''B'' produces response ''Y'', then input (''A'' + ''B'') produces response (''X'' + ''Y''). A function F(x) that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity F(x_1 + x_2) = F(x_1) + F(x_2) and homogeneity F(ax) = a F(x) for scalar . This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as :a_1x_1+\cdots +a_nx_n=b, linear maps such as :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrix (mathematics), matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as line (geometry), lines, plane (geometry), planes and rotation (mathematics), rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to Space of functions, function spaces. Linear algebra is also used in most sciences and fields of engineering because it allows mathematical model, modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Shifter Using IQ Modulator
Phase or phases may refer to: Science *State of matter, or phase, one of the distinct forms in which matter can exist *Phase (matter), a region of space throughout which all physical properties are essentially uniform *Phase space, a mathematical space in which each possible state of a physical system is represented by a point also referred to as a "microscopic state" ** Phase space formulation, a formulation of quantum mechanics in phase space *Phase (waves), the position of a point in time (an instant) on a waveform cycle **Instantaneous phase, generalization for both cyclic and non-cyclic phenomena * AC phase, the phase offset between alternating current electric power in multiple conducting wires **Single-phase electric power, distribution of AC electric power in a system where the voltages of the supply vary in unison **Three-phase electric power, a common method of AC electric power generation, transmission, and distribution *Phase problem, the loss of information (the phase ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Shift
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly sc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |