|
Peter J. Olver
Peter John Olver (11 January 1952, Twickenham) is a British-American mathematician working in differential geometry. Education and career After moving to the USA in 1961, Olver obtained a bachelor's degree in Applied Mathematics at Brown University in 1973 and a PhD in Mathematics at Harvard University in 1976. His PhD thesis was entitled "''Symmetry Groups of Partial Differential Equations"'' and was written under the supervision of Garrett Birkhoff. He worked as a L.E. Dickson Instructor in Mathematics at University of Chicago (1976-1978) and as a research fellow at University of Oxford (1978-1980). He then moved to University of Minnesota as assistant professor, and he became full professor in the same university in 1985. Between 1992 and 1993 he was professor at University of Maryland. Olver was member of the board of directors of Foundations of Computational Mathematics from 2002 to 2014. He was elected fellow of the American Mathematical Society in 2013 and of the Socie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Middlesex
Middlesex (; abbreviation: Middx) is a Historic counties of England, former county in South East England, now mainly within Greater London. Its boundaries largely followed three rivers: the River Thames, Thames in the south, the River Lea, Lea to the east and the River Colne, Hertfordshire, Colne to the west. A line of hills formed its northern boundary with Hertfordshire. The county was the List of counties of England by area in 1831, second smallest of the historic counties of England, after Rutland. The name of the county derives from its origin as a homeland for the Middle Saxons in the early Middle Ages, with the county subsequently part of that territory in the ninth or tenth century. The City of London, formerly part of the county, became a self governing county corporate in the twelfth century; the City was still able to exert influence as the sheriffs of London maintained their jurisdiction in Middlesex, though the county otherwise remained separate. To the east of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Society For Industrial And Applied Mathematics
Society for Industrial and Applied Mathematics (SIAM) is a professional society dedicated to applied mathematics, computational science, and data science through research, publications, and community. SIAM is the world's largest scientific society devoted to applied mathematics, and roughly two-thirds of its membership resides within the United States. Founded in 1951, the organization began holding annual national meetings in 1954, and now hosts conferences, publishes books and scholarly journals, and engages in advocacy in issues of interest to its membership. Members include engineers, scientists, and mathematicians, both those employed in academia and those working in industry. The society supports educational institutions promoting applied mathematics. SIAM is one of the four member organizations of the Joint Policy Board for Mathematics. Membership Membership is open to both individuals and organizations. By the end of its first full year of operation, SIAM had 130 me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
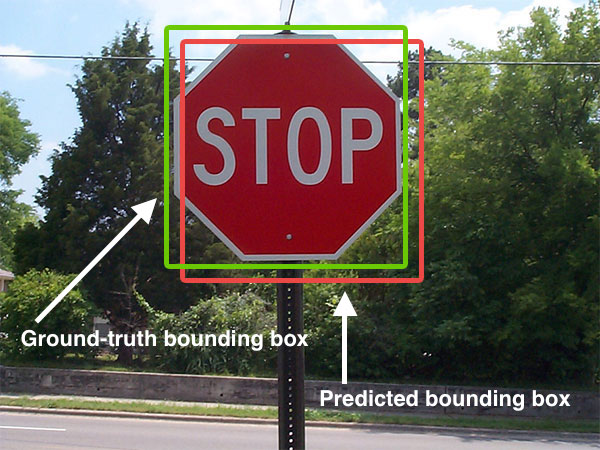
Computer Vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the form of decisions. "Understanding" in this context signifies the transformation of visual images (the input to the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scientific discipline of computer vision is concerned with the theory behind artificial systems that extract information from images. Image data can take many forms, such as video sequences, views from multiple cameras, multi-dimensional data from a 3D scanning, 3D scanner, 3D point clouds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image Processing
An image or picture is a visual representation. An image can be two-dimensional, such as a drawing, painting, or photograph, or three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a projection on a surface, activation of electronic signals, or digital displays; they can also be reproduced through mechanical means, such as photography, printmaking, or photocopying. Images can also be animated through digital or physical processes. In the context of signal processing, an image is a distributed amplitude of color(s). In optics, the term ''image'' (or ''optical image'') refers specifically to the reproduction of an object formed by light waves coming from the object. A ''volatile image'' exists or is perceived only for a short period. This may be a reflection of an object by a mirror, a projection of a camera obscura, or a scene displayed on a cathode-ray tube. A ''fixed image'', also called a hard copy, is one that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the profession, professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of Mathematical analysis, applied analysis, most notably differential equations; approximation theory (broadly construed, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudogroup
In mathematics, a pseudogroup is a set of homeomorphisms between open sets of a space, satisfying group-like and sheaf-like properties. It is a generalisation of the concept of a transformation group, originating however from the geometric approach of Sophus Lie to investigate symmetries of differential equations, rather than out of abstract algebra (such as quasigroup, for example). The modern theory of pseudogroups was developed by Élie Cartan in the early 1900s. Definition A pseudogroup imposes several conditions on sets of homeomorphisms (respectively, diffeomorphisms) defined on open sets of a given Euclidean space or more generally of a fixed topological space (respectively, smooth manifold). Since two homeomorphisms and compose to a homeomorphism from to , one asks that the pseudogroup is closed under composition and inversion. However, unlike those for a group, the axioms defining a pseudogroup are not purely algebraic; the further requirements are related to the pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Invariant
In mathematics, a differential invariant is an invariant for the action of a Lie group on a space that involves the derivatives of graphs of functions in the space. Differential invariants are fundamental in projective differential geometry, and the curvature is often studied from this point of view. Differential invariants were introduced in special cases by Sophus Lie in the early 1880s and studied by Georges Henri Halphen at the same time. was the first general work on differential invariants, and established the relationship between differential invariants, invariant differential equations, and invariant differential operators. Differential invariants are contrasted with geometric invariants. Whereas differential invariants can involve a distinguished choice of independent variables (or a parameterization), geometric invariants do not. The moving frames method, which is a refinement of Élie Cartan's method of moving frames, gives several new powerful tools for finding and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartan's Equivalence Method
In mathematics, Cartan's equivalence method is a technique in differential geometry for determining whether two geometrical structures are the same up to a diffeomorphism. For example, if ''M'' and ''N'' are two Riemannian manifolds with metrics ''g'' and ''h'', respectively, when is there a diffeomorphism :\phi:M\rightarrow N such that :\phi^*h=g? Although the answer to this particular question was known in dimension 2 to Gauss and in higher dimensions to Christoffel and perhaps Riemann as well, Élie Cartan and his intellectual heirs developed a technique for answering similar questions for radically different geometric structures. (For example see the Cartan–Karlhede algorithm.) Cartan successfully applied his equivalence method to many such structures, including projective structures, CR structures, and complex structures, as well as ostensibly non-geometrical structures such as the equivalence of Lagrangians and ordinary differential equations. (His techniques wer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moving Frame
In mathematics, a moving frame is a flexible generalization of the notion of a coordinate frame (an ordered basis of a vector space, in conjunction with an origin) often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space. Introduction In lay terms, a ''frame of reference'' is a system of measuring rods used by an observer to measure the surrounding space by providing coordinates. A moving frame is then a frame of reference which moves with the observer along a trajectory (a curve). The method of the moving frame, in this simple example, seeks to produce a "preferred" moving frame out of the kinematic properties of the observer. In a geometrical setting, this problem was solved in the mid 19th century by Jean Frédéric Frenet and Joseph Alfred Serret. The Frenet–Serret frame is a moving frame defined on a curve which can be constructed purely from the velocity and acceleration of the curve. The Frenet–Serret ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry Group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object ''X'' is ''G'' = Sym(''X''). For an object in a metric space, its symmetries form a subgroup of the isometry group of the ambient space. This article mainly considers symmetry groups in Euclidean geometry, but the concept may also be studied for more general types of geometric structure. Introduction We consider the "objects" possessing symmetry to be geometric figures, images, and patterns, such as a wallpaper pattern. For symmetry of physical objects, one may also take their physical composition as part of the pattern. (A pattern may be specified formally as a scalar field, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be thought of as a "transformation" in the abstract sense, for instance multiplication and the taking of inverses (to allow division), or equivalently, the concept of addition and subtraction. Combining these two ideas, one obtains a continuous group where multiplying points and their inverses is continuous. If the multiplication and taking of inverses are smoothness, smooth (differentiable) as well, one obtains a Lie group. Lie groups provide a natural model for the concept of continuous symmetry, a celebrated example of which is the circle group. Rotating a circle is an example of a continuous symmetry. For an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |