|
Periodogram For Proxima Centauri B
In signal processing, a periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898. Today, the periodogram is a component of more sophisticated methods (see spectral estimation). It is the most common tool for examining the amplitude vs frequency characteristics of FIR filters and window functions. FFT spectrum analyzers are also implemented as a time-sequence of periodograms. Definition There are at least two different definitions in use today. One of them involves time-averaging, and one does not. Time-averaging is also the purview of other articles (Bartlett's method and Welch's method). This article is not about time-averaging. The definition of interest here is that the power spectral density of a continuous function, , is the Fourier transform of its auto-correlation function (see Cross-correlation theorem, Spectral density, and Wiener–Khinchin theorem): \mathcal\ = X(f)\cdot X^*(f) = \left, X(f) \^2. Computation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
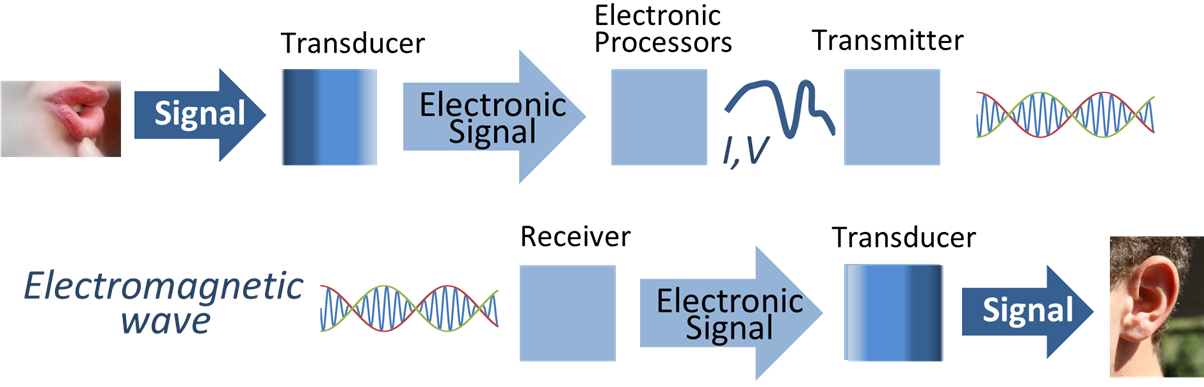
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodogram For Proxima Centauri B
In signal processing, a periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898. Today, the periodogram is a component of more sophisticated methods (see spectral estimation). It is the most common tool for examining the amplitude vs frequency characteristics of FIR filters and window functions. FFT spectrum analyzers are also implemented as a time-sequence of periodograms. Definition There are at least two different definitions in use today. One of them involves time-averaging, and one does not. Time-averaging is also the purview of other articles (Bartlett's method and Welch's method). This article is not about time-averaging. The definition of interest here is that the power spectral density of a continuous function, , is the Fourier transform of its auto-correlation function (see Cross-correlation theorem, Spectral density, and Wiener–Khinchin theorem): \mathcal\ = X(f)\cdot X^*(f) = \left, X(f) \^2. Computation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NIST
The National Institute of Standards and Technology (NIST) is an agency of the United States Department of Commerce whose mission is to promote American innovation and industrial competitiveness. NIST's activities are organized into physical science laboratory programs that include nanoscale science and technology, engineering, information technology, neutron research, material measurement, and physical measurement. From 1901 to 1988, the agency was named the National Bureau of Standards. History Background The Articles of Confederation, ratified by the colonies in 1781, provided: The United States in Congress assembled shall also have the sole and exclusive right and power of regulating the alloy and value of coin struck by their own authority, or by that of the respective states—fixing the standards of weights and measures throughout the United States. Article 1, section 8, of the Constitution of the United States, ratified in 1789, granted these powers to the new Co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SAMV (algorithm)
SAMV (iterative sparse asymptotic minimum variance) is a parameter-free superresolution algorithm for the linear inverse problem in spectral estimation, direction-of-arrival (DOA) estimation and tomographic reconstruction with applications in signal processing, medical imaging and remote sensing. The name was coined in 2013 to emphasize its basis on the asymptotically minimum variance (AMV) criterion. It is a powerful tool for the recovery of both the amplitude and frequency characteristics of multiple highly correlated sources in challenging environments (e.g., limited number of snapshots and low signal-to-noise ratio). Applications include synthetic-aperture radar, computed tomography scan, and magnetic resonance imaging (MRI). Definition The formulation of the SAMV algorithm is given as an inverse problem in the context of DOA estimation. Suppose an M-element uniform linear array (ULA) receive K narrow band signals emitted from sources located at locations \mathbf = \, re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Super-resolution Imaging
Super-resolution imaging (SR) is a class of techniques that improve the resolution of an imaging system. In optical SR the diffraction limit of systems is transcended, while in geometrical SR the resolution of digital imaging sensors is enhanced. In some radar and sonar imaging applications (e.g. magnetic resonance imaging (MRI), high-resolution computed tomography), subspace decomposition-based methods (e.g. MUSIC) and compressed sensing-based algorithms (e.g., SAMV) are employed to achieve SR over standard periodogram algorithm. Super-resolution imaging techniques are used in general image processing and in super-resolution microscopy. Basic concepts Because some of the ideas surrounding super-resolution raise fundamental issues, there is need at the outset to examine the relevant physical and information-theoretical principles: * Diffraction limit: The detail of a physical object that an optical instrument can reproduce in an image has limits that are mandated by laws ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MUSIC (algorithm)
MUSIC (multiple sIgnal classification) is an algorithm used for frequency estimation and radio direction finding.Schmidt, R.O,Multiple Emitter Location and Signal Parameter Estimation" IEEE Trans. Antennas Propagation, Vol. AP-34 (March 1986), pp. 276–280. History In many practical signal processing problems, the objective is to estimate from measurements a set of constant parameters upon which the received signals depend. There have been several approaches to such problems including the so-called maximum likelihood (ML) method of Capon (1969) and Burg's maximum entropy (ME) method. Although often successful and widely used, these methods have certain fundamental limitations (especially bias and sensitivity in parameter estimates), largely because they use an incorrect model (e.g., AR rather than special ARMA) of the measurements. Pisarenko (1973) was one of the first to exploit the structure of the data model, doing so in the context of estimation of parameters of c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least-squares Spectral Analysis
Least-squares spectral analysis (LSSA) is a method of estimating a Spectral density estimation#Overview, frequency spectrum based on a least-squares fit of Sine wave, sinusoids to data samples, similar to Fourier analysis. Fourier analysis, the most used spectral method in science, generally boosts long-periodic noise in the long and gapped records; LSSA mitigates such problems. Unlike in Fourier analysis, data need not be equally spaced to use LSSA. Developed in 1969 and 1971, LSSA is also known as the Vaníček method and the Gauss-Vaniček method after Petr Vaníček, and as the Lomb method or the Lomb–Scargle periodogram, based on the simplifications first by Nicholas R. Lomb and then by Jeffrey D. Scargle. Historical background The close connections between Fourier analysis, the periodogram, and the least-squares fitting of sinusoids have been known for a long time. However, most developments are restricted to complete data sets of equally spaced samples. In 1963, Free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matched Filter
In signal processing, the output of the matched filter is given by correlating a known delayed signal, or ''template'', with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template. The matched filter is the optimal linear filter for maximizing the signal-to-noise ratio (SNR) in the presence of additive stochastic noise. Matched filters are commonly used in radar, in which a known signal is sent out, and the reflected signal is examined for common elements of the out-going signal. Pulse compression is an example of matched filtering. It is so called because the impulse response is matched to input pulse signals. Two-dimensional matched filters are commonly used in image processing, e.g., to improve the SNR of X-ray observations. Additional applications of note are in seismology and gravitational-wave astronomy. Matched filtering is a demodulation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Density Estimation
In statistical signal processing, the goal of spectral density estimation (SDE) or simply spectral estimation is to estimate the spectral density (also known as the power spectral density) of a signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities. Some SDE techniques assume that a signal is composed of a limited (usually small) number of generating frequencies plus noise and seek to find the location and intensity of the generated frequencies. Others make no assumption on the number of components and seek to estimate the whole generating spectrum. Overview Spectrum analysis, also referred to as frequency domain analysis or spectral density estimation, is the technical process of decomposing a complex signal into s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. In smoothing, the data points of a signal are modified so individual points higher than the adjacent points (presumably because of noise) are reduced, and points that are lower than the adjacent points are increased leading to a smoother signal. Smoothing may be used in two important ways that can aid in data analysis (1) by being able to extract more information from the data as long as the assumption of smoothing is reasonable and (2) by being able to provide analyses that are both flexible and robust. Many different algorithms are used in smoothing. Compared to curve fitting Smoothing may be distinguished from the related and partially overlapping concept of curve fitting in the following ways: * curve fitting often involves the use of an explicit functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Process
In mathematics and statistics, a stationary process (also called a strict/strictly stationary process or strong/strongly stationary process) is a stochastic process whose statistical properties, such as mean and variance, do not change over time. More formally, the joint probability distribution of the process remains the same when shifted in time. This implies that the process is statistically consistent across different time periods. Because many statistical procedures in time series analysis assume stationarity, non-stationary data are frequently transformed to achieve stationarity before analysis. A common cause of non-stationarity is a trend in the mean, which can be due to either a unit root or a deterministic trend. In the case of a unit root, stochastic shocks have permanent effects, and the process is not mean-reverting. With a deterministic trend, the process is called trend-stationary, and shocks have only transitory effects, with the variable tending towards a determin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |