|
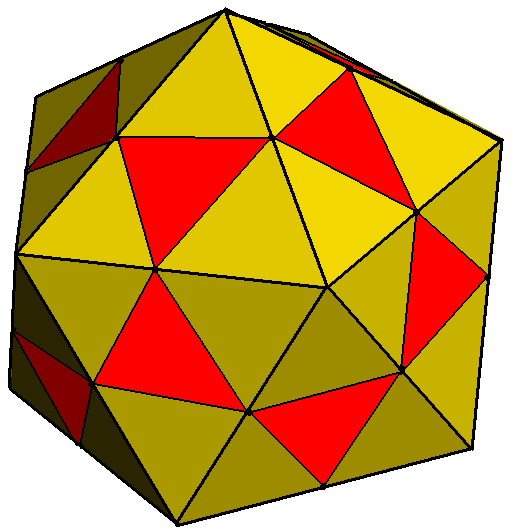
Pentakis Icosidodecahedron
In geometry, the pentakis icosidodecahedron or subdivided icosahedron is a convex polyhedron with 80 triangular faces, 120 edges, and 42 vertices. It is a dual of the ''truncated rhombic triacontahedron'' (chamfered dodecahedron). Construction Its name comes from a topological construction from the icosidodecahedron with the kis operator applied to the pentagonal faces. In this construction, all the vertices are assumed to be the same distance from the center, while in general icosahedral symmetry can be maintained even with the 12 order-5 vertices at a different distance from the center as the other 30. It can also be topologically constructed from the icosahedron, dividing each triangular face into 4 triangles by adding mid-edge vertices. From this construction, all 80 triangles will be equilateral, but faces will be coplanar. Related polyhedra File:Icosidodecahedron.png, Icosidodecahedron File:Pentakisdodecahedron.jpg, Pentakis dodecahedron is a slightly smaller Ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesic Polyhedron
A geodesic polyhedron is a convex polyhedron made from triangles. They usually have icosahedral symmetry, such that they have 6 triangles at a vertex, except 12 vertices which have 5 triangles. They are the dual of corresponding Goldberg polyhedra with mostly hexagonal faces. Geodesic polyhedra are a good approximation to a sphere for many purposes, and appear in many different contexts. The most well-known may be the geodesic domes designed by Buckminster Fuller, which geodesic polyhedra are named after. Geodesic grids used in geodesy also have the geometry of geodesic polyhedra. The capsids of some viruses have the shape of geodesic polyhedra, and fullerene molecules have the shape of Goldberg polyhedra. Geodesic polyhedra are available as geometric primitives in the Blender 3D modeling software package, which calls them icospheres: they are an alternative to the UV sphere, having a more regular distribution of vertices than the UV sphere. The Goldberg–Coxeter construction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the (convex, non-stellated) regular icosahedron—one of the Platonic solids—whose faces are 20 equilateral triangles. Regular icosahedra There are two objects, one convex and one nonconvex, that can both be called regular icosahedra. Each has 30 edges and 20 equilateral triangle faces with five meeting at each of its twelve vertices. Both have icosahedral symmetry. The term "regular icosahedron" generally refers to the convex variety, while the nonconvex form is called a ''great icosahedron''. Convex regular icosahedron The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular Platonic solids, and is represented by its Schläfli symbol , co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrakis Cuboctahedron
In geometry, the tetrakis cuboctahedron is a convex polyhedron with 32 triangular faces, 48 edges, and 18 vertices. It is a dual of the truncated rhombic dodecahedron. Its name comes from a topological construction from the cuboctahedron with the kis operator applied to the square faces. In this construction, all the vertices are assumed to be the same distance from the center, while in general octahedral symmetry can be maintain even with the 6 order-4 vertices at a different distance from the center as the other 12. Related polyhedra It can also be topologically constructed from the octahedron, dividing each triangular face into 4 triangles by adding mid-edge vertices (an ortho operation). From this construction, all 32 triangles will be equilateral. This polyhedron can be confused with a slightly smaller Catalan solid, the tetrakis hexahedron, which has only 24 triangles, 32 edges, and 14 vertices. File:Tetrakis cuboctahedron on octahedron.png, Octahedron with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Regular 4-polytope
In mathematics, a regular 4-polytope is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions. There are six convex and ten star regular 4-polytopes, giving a total of sixteen. History The convex regular 4-polytopes were first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. He discovered that there are precisely six such figures. Schläfli also found four of the regular star 4-polytopes: the grand 120-cell, great stellated 120-cell, grand 600-cell, and great grand stellated 120-cell. He skipped the remaining six because he would not allow forms that failed the Euler characteristic on cells or vertex figures (for zero-hole tori: ''F'' − ''E'' + ''V'' 2). That excludes cells and vertex figures such as the great dodecahedron and small stellated dodecahedron . Edmund Hess (1843–1903) publi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from "tetrahedral complex") and a polytetrahedron, being bounded by tetrahedral cells. The 600-cell's boundary is composed of 600 tetrahedral cells with 20 meeting at each vertex. Together they form 1200 triangular faces, 720 edges, and 120 vertices. It is the 4- dimensional analogue of the icosahedron, since it has five tetrahedra meeting at every edge, just as the icosahedron has five triangles meeting at every vertex. Its dual polytope is the 120-cell. Geometry The 600-cell is the fifth in the sequence of 6 convex regular 4-polytopes (in order of size and complexity). It can be deconstructed into twenty-five overlapping instances of its immediate predecessor the 24-cell, as the 24-cell can be deconstructed into three overlapping in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Projection
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P : V \to V such that P^2 = P. When V has an inner product and is complete (i.e. when V is a Hilbert space) the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Pyramid
In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point (the apex). Like any pyramid, it is self- dual. The ''regular'' pentagonal pyramid has a base that is a regular pentagon and lateral faces that are equilateral triangles. It is one of the Johnson solids (). It can be seen as the "lid" of an icosahedron; the rest of the icosahedron forms a gyroelongated pentagonal pyramid, More generally an order-2 vertex-uniform pentagonal pyramid can be defined with a regular pentagonal base and 5 isosceles triangle sides of any height. Cartesian coordinates The pentagonal pyramid can be seen as the "lid" of a regular icosahedron; the rest of the icosahedron forms a gyroelongated pentagonal pyramid, ''J''11. From the Cartesian coordinates of the icosahedron, Cartesian coordinates for a pentagonal pyramid with edge length 2 may be inferred as :(1,0,\tau),\,(-1,0,\tau),\,(0,\tau,1),\,(\tau,1,0),(\tau,-1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Icosihemidodecahedron
In geometry, the small icosihemidodecahedron (or small icosahemidodecahedron) is a uniform star polyhedron, indexed as . It has 26 faces (20 triangles and 6 decagons), 60 edges, and 30 vertices. Its vertex figure alternates two regular triangles and decagons as a crossed quadrilateral. It is a hemipolyhedron with its six decagonal faces passing through the model center. It is given a Wythoff symbol, but that construction represents a double covering of this model. Related polyhedra It shares its edge arrangement with the icosidodecahedron (its convex hull, having the triangular faces in common), and with the small dodecahemidodecahedron (having the decagonal faces in common). See also * Pentakis icosidodecahedron * List of uniform polyhedra In geometry, a uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive ( transitive on its vertices, isogonal, i.e. there is an isometry mapping any vertex onto any other). It follows tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleetope
In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope is another polyhedron or polytope formed by replacing each facet of with a shallow pyramid. Kleetopes are named after Victor Klee. Examples The triakis tetrahedron is the Kleetope of a tetrahedron, the triakis octahedron is the Kleetope of an octahedron, and the triakis icosahedron is the Kleetope of an icosahedron. In each of these cases the Kleetope is formed by adding a triangular pyramid to each face of the original polyhedron. The tetrakis hexahedron is the Kleetope of the cube, formed by adding a square pyramid to each of its faces, and the pentakis dodecahedron is the Kleetope of the dodecahedron, formed by adding a pentagonal pyramid to each face of the dodecahedron. The base polyhedron of a Kleetope does not need to be a Platonic solid. For instance, the disdyakis dodecahedron is the Kleetope of the rhombic dodecahedron, formed by replacing each rhombus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan Solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. There are 13 Catalan solids. They are named for the Belgian mathematician Eugène Catalan, who first described them in 1865. The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic solids and Archimedean solids, the faces of Catalan solids are ''not'' regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Being face-transitive, Catalan solids are isohedra. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids. Just as prisms and antiprisms are generally not considered Archimedean solids, so bipyramids and trapezohedra are generally n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentakis Dodecahedron
In geometry, a pentakis dodecahedron or kisdodecahedron is the polyhedron created by attaching a pentagonal pyramid to each face of a regular dodecahedron; that is, it is the Kleetope of the dodecahedron. It is a Catalan solid, meaning that it is a dual of an Archimedean solid, in this case, the truncated icosahedron. Cartesian coordinates Let \phi be the golden ratio. The 12 points given by (0, \pm 1, \pm \phi) and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the points (\pm 1, \pm 1, \pm 1) together with the points (\pm\phi, \pm 1/\phi, 0) and cyclic permutations of these coordinates. Multiplying all coordinates of the icosahedron by a factor of (3\phi+12)/19\approx 0.887\,057\,998\,22 gives a slightly smaller icosahedron. The 12 vertices of this icosahedron, together with the vertices of the dodecahedron, are the vertices of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty (''icosi'') triangular faces and twelve (''dodeca'') pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron. Geometry An icosidodecahedron has icosahedral symmetry, and its first stellation is the compound of a dodecahedron and its dual icosahedron, with the vertices of the icosidodecahedron located at the midpoints of the edges of either. Its dual polyhedron is the rhombic triacontahedron. An icosidodecahedron can be split along any of six planes to form a pair of pentagonal rotundae, which belong among the Johnson solids. The icosidodecahedron can be considered a ''pentagonal gyrobirotunda'', as a combination of two rotundae (compare pentagonal orthobirotunda, one of the Johnso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |