|
Pentagonal Rotunda
The pentagonal rotunda is a convex polyhedron with regular polygonal faces. These faces comprise ten equilateral triangles, six regular pentagons, and one regular decagon, making a total of seventeen. The pentagonal rotunda is an example of Johnson solid, enumerated as the sixth Johnson solid J_6 . It is another example of a elementary polyhedron because by slicing it with a plane, the resulting smaller convex polyhedra do not have regular faces. The pentagonal rotunda can be regarded as half of an icosidodecahedron, an Archimedean solid, or as half of a pentagonal orthobirotunda, another Johnson solid. Both polyhedrons are constructed by attaching two pentagonal rotundas base-to-base. The difference is one of the pentagonal rotundas is twisted. Other Johnson solids constructed by attaching to the base of a pentagonal rotunda are elongated pentagonal rotunda, gyroelongated pentagonal rotunda, pentagonal orthocupolarotunda, pentagonal gyrocupolarotunda, elongated pentagonal orthoc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, solids with such a property: the first solids are the Pyramid (geometry), pyramids, Cupola (geometry), cupolas, and a Rotunda (geometry), rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. Definition and background A Johnson solid is a convex polyhedron whose faces are all regular polygons. The convex polyhedron means as bounded intersections of finitely many Half-space (geometry), half-spaces, or as the convex hull of finitely many points. Although there is no restriction that any given regular polygon cannot be a face of a Johnson solid, some authors required that Johnson solids are not Uniform polyhedron, uniform. This means that a Johnson solid is not a Platonic solid, Arc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
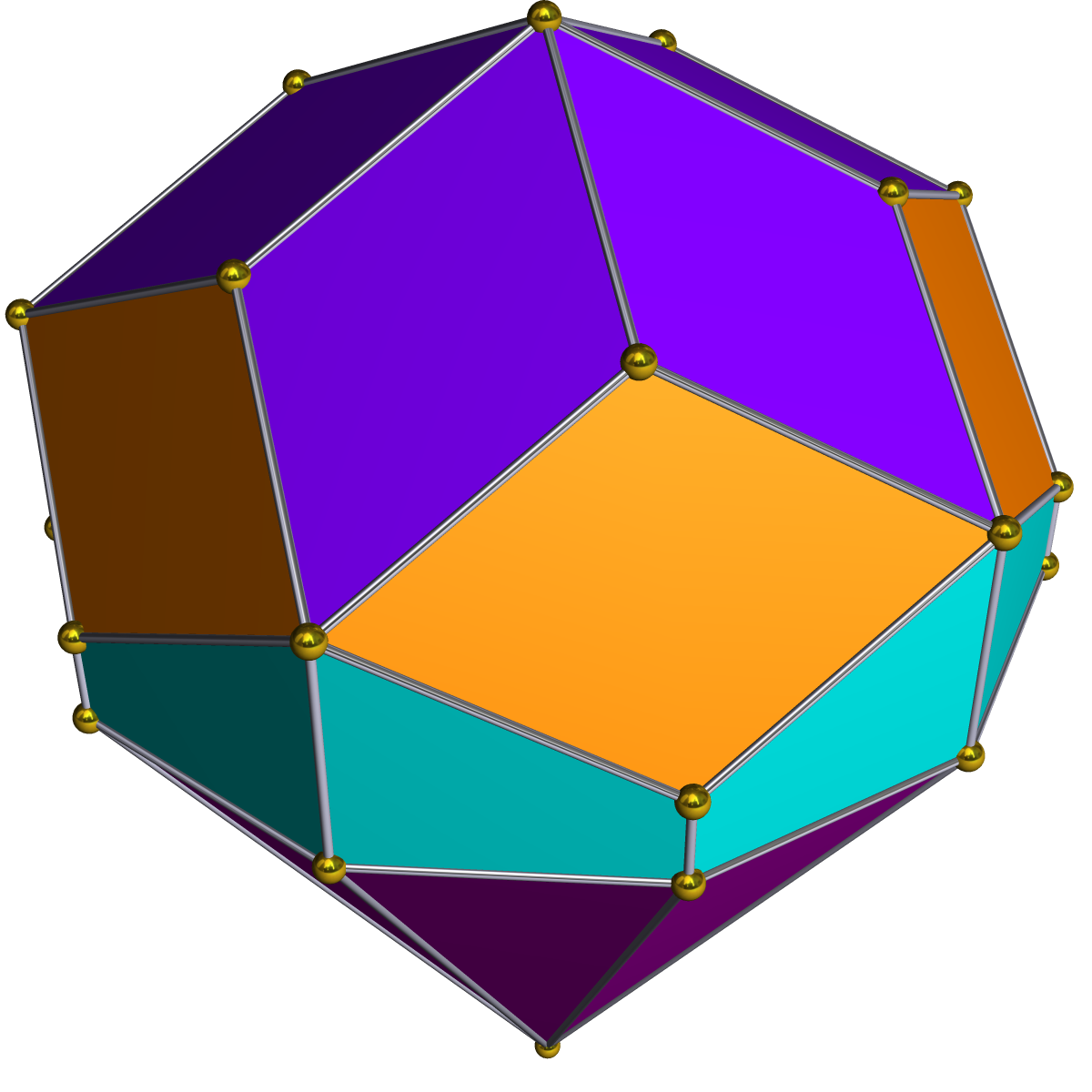
Archimedean Solid
The Archimedean solids are a set of thirteen convex polyhedra whose faces are regular polygon and are vertex-transitive, although they aren't face-transitive. The solids were named after Archimedes, although he did not claim credit for them. They belong to the class of uniform polyhedra, the polyhedra with regular faces and symmetric vertices. Some Archimedean solids were portrayed in the works of artists and mathematicians during the Renaissance. The elongated square gyrobicupola or ' is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive. The solids The Archimedean solids have a single vertex configuration and highly symmetric properties. A vertex configuration indicates which regular polygons meet at each vertex. For instance, the configuration 3 \cdot 5 \cdot 3 \cdot 5 indicates a polyhedron in which each vertex is met by alternating two triangles and two pentagons. Highl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyroelongated Pentagonal Cupolarotunda
In geometry, the gyroelongated pentagonal cupolarotunda is one of the Johnson solids (). As the name suggests, it can be constructed by gyroelongating a pentagonal cupolarotunda ( or ) by inserting a decagonal antiprism between its two halves. The gyroelongated pentagonal cupolarotunda is one of five Johnson solids which are chiral Chirality () is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek language, Greek (''kheir''), "hand", a familiar chiral object. An object or a system is ''chiral'' if it is dist ..., meaning that they have a "left-handed" and a "right-handed" form. In the illustration to the right, each pentagonal face on the bottom half of the figure is connected by a path of two triangular faces to a square face above it and to the left. In the figure of opposite chirality (the mirror image of the illustrated figure), each bottom pentagon would be connected to a square face above it and to the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Gyrobirotunda
In geometry, the elongated pentagonal gyrobirotunda or elongated icosidodecahedron is one of the Johnson solids (). As the name suggests, it can be constructed by elongating a "pentagonal gyrobirotunda," or icosidodecahedron (one of the Archimedean solids), by inserting a decagonal prism between its congruent halves. Rotating one of the pentagonal rotundae () through 36 degrees before inserting the prism yields an elongated pentagonal orthobirotunda (). Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal gyrobirotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 26, 2010. :V=\frac\left(45+17\sqrt+15\sqrt\right)a^3 \approx 21.52 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Orthobirotunda
In geometry, the elongated pentagonal orthobirotunda is one of the Johnson solids (). Its Conway polyhedron notation iat5jP5 As the name suggests, it can be constructed by elongating a pentagonal orthobirotunda () by inserting a decagonal prism between its congruent halves. Rotating one of the pentagonal rotundae () through 36 degrees before inserting the prism yields the elongated pentagonal gyrobirotunda (). Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal orthobirotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 26, 2010. :V=\frac\left(45+17\sqrt+15\sqrt\right)a^3\approx21.5297...a^3 :A=\left(10+\sqrt\right)a^2\approx39 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Gyrocupolarotunda
In geometry, the elongated pentagonal gyrocupolarotunda is one of the Johnson solids (). As the name suggests, it can be constructed by elongating a pentagonal gyrocupolarotunda () by inserting a decagonal prism between its halves. Rotating either the pentagonal cupola () or the pentagonal rotunda () through 36 degrees before inserting the prism yields an elongated pentagonal orthocupolarotunda (). Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal gyrocupolarotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 25, 2010. :V=\frac\left(11+5\sqrt+6\sqrt\right)a^3\approx16.936...a^3 :A=\frac\left(60+\sqrt\right)a^2\approx33.5385 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Orthocupolarotunda
In geometry, the elongated pentagonal orthocupolarotunda is one of the Johnson solids (). As the name suggests, it can be constructed by elongating a pentagonal orthocupolarotunda () by inserting a decagonal prism between its halves. Rotating either the cupola or the rotunda through 36 degrees before inserting the prism yields an elongated pentagonal gyrocupolarotunda (). Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal orthocupolarotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 25, 2010. :V=\frac\left(11+5\sqrt+6\sqrt\right)a^3\approx16.936...a^3 :A=\frac\left(60+\sqrt\right)a^2\approx33.5385...a^2 References External link ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Gyrocupolarotunda
In geometry, the pentagonal gyrocupolarotunda is one of the Johnson solids (). Like the pentagonal orthocupolarotunda (), it can be constructed by joining a pentagonal cupola () and a pentagonal rotunda () along their decagonal bases. The difference is that in this solid, the two halves are rotated 36 degrees with respect to one another. Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Pentagonal gyrocupolarotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 24, 2010. :V=\frac\left(11+5\sqrt\right)a^3\approx9.24181...a^3 :A= \left(5+\frac\sqrt+\frac\sqrt\right) a^2\approx23.5385...a^2 References External links * Johnson solids {{Polyhedro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Orthocupolarotunda
In geometry, the pentagonal orthocupolarotunda is one of the Johnson solids (). As the name suggests, it can be constructed by joining a pentagonal cupola () and a pentagonal rotunda () along their decagonal bases, matching the pentagonal faces. A 36-degree rotation of one of the halves before the joining yields a pentagonal gyrocupolarotunda (). Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Pentagonal orthocupolarotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 24, 2010. :V=\frac\left(11+5\sqrt\right)a^3\approx9.24181...a^3 :A=\left(5+\frac\sqrt\right)a^2\approx23.5385...a^2 References External links * {{Polyhedron-stub Johnson solid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyroelongated Pentagonal Rotunda
In geometry, the gyroelongated pentagonal rotunda is one of the Johnson solids (''J''25). As the name suggests, it can be constructed by gyroelongating a pentagonal rotunda (''J''6) by attaching a decagonal antiprism to its base. It can also be seen as a gyroelongated pentagonal birotunda (''J''48) with one pentagonal rotunda removed. Area and Volume With edge length a, the surface area is :A=\frac\left( 15\sqrt+\left(5+3\sqrt\right)\sqrt\right)a^2\approx31.007454303...a^2, and the volume is :V=\left(\frac+\frac\sqrt + \frac\sqrt\right) a^3\approx13.667050844...a^3. Dual polyhedron The dual of the gyroelongated pentagonal rotunda has 30 faces: 10 pentagons, 10 rhombi, and 10 quadrilaterals. External links * {{Johnson solids navigator Johnson solids ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Rotunda
In geometry, the elongated pentagonal rotunda is one of the Johnson solids (''J''21). As the name suggests, it can be constructed by elongating a pentagonal rotunda (''J''6) by attaching a decagonal prism to its base. It can also be seen as an elongated pentagonal orthobirotunda (''J''42) with one pentagonal rotunda removed. Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal rotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 22, 2010. V=\frac\left(45+17\sqrt+30\sqrt\right)a^3\approx14.612...a^3 A=\frac\left(20+\sqrt\right)a^2\approx32.3472...a^2 Dual polyhedron The dual of the elongated pentagonal rotunda has 30 faces: 10 isos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Orthobirotunda
In geometry, the pentagonal orthobirotunda is a polyhedron constructed by attaching two pentagonal rotundae along their decagonal faces, matching like faces. It is an example of Johnson solid. Construction The pentagonal orthobirotunda is constructed by attaching two pentagonal rotundas to their base, covering decagon faces. The resulting polyhedron has 32 faces, 30 vertices, and 60 edges. This construction is similar to icosidodecahedron (or pentagonal gyrobirotunda), an Archimedean solid: the difference is one of its rotundas twisted around 36°, making the pentagonal faces connect to the triangular one, a process known as gyration. A convex polyhedron in which all of the faces are regular polygons is the Johnson solid In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s .... The pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |