|
Pentagonal Bifrustum
In geometry, the pentagonal bifrustum or truncated pentagonal bipyramid is the third in an infinite series of bifrustum polyhedra. It has 10 trapezoidal and 2 pentagonal faces. Constructions The pentagonal bifrustum is the dual polyhedron of a Johnson solid, the elongated pentagonal bipyramid. This polyhedron can be constructed by taking a pentagonal bipyramid and truncating the polar axis vertices. In Conway polyhedron notation, it can be represented as the polyhedron "", meaning the truncation of the degree-five vertices of the dual of a pentagonal prism. Alternatively, it can be constructed by gluing together two end-to-end pentagonal frustums, or (if coplanar faces are allowed) by gluing together two pentagonal prisms on their pentagonal faces. Application In nanoparticles, a 15-site truncated pentagonal bipyramid structure may form the nucleus of larger twinned structures with five-fold or icosahedral In geometry, an icosahedron ( or ) is a polyhedron with 20 face ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifrustum
In geometry, an -agonal bifrustum is a polyhedron composed of three parallel planes of -agons, with the middle plane largest and usually the top and bottom congruent. It can be constructed as two congruent frusta combined across a plane of symmetry, and also as a bipyramid with the two polar vertices truncated. They are duals to the family of elongated bipyramids. Formulae For a regular -gonal bifrustum with the equatorial polygon sides , bases sides and semi-height (half the distance between the planes of bases) , the lateral surface area , total area and volume are: and \begin A_l &= n (a+b) \sqrt \\ pt A &= A_l + n \frac \\ pt V &= n \frach \end Note that the volume V is twice the volume of a frusta. Forms Three bifrusta are duals to three Johnson solid In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Bipyramid
The pentagonal bipyramid (or pentagonal dipyramid) is a polyhedron with ten triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an example of deltahedra, composite polyhedron, and Johnson solid. The pentagonal bipyramid may be represented as four-connected well-covered graph. This polyhedron may be used in the chemical compound as the description of an atom cluster known as pentagonal bipyramidal molecular geometry, as a solution in Thomson problem, as well as in decahedral nanoparticles. Special cases As a right bipyramid Like other bipyramids, the pentagonal bipyramid can be constructed by attaching the base of two pentagonal pyramids. These pyramids cover their pentagonal base, such that the resulting polyhedron has ten triangles as its faces, fifteen edges, and seven vertices. The pentagonal bipyramid is said to be right if the pyramids are symmetri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fiveling
A fiveling, also known as a decahedral nanoparticle, a multiply-twinned particle (MTP), a pentagonal nanoparticle, a pentatwin, or a five-fold twin is a type of twinned crystal that can exist at sizes ranging from nanometers to millimetres. It contains five different single crystals arranged around a common axis. In most cases each unit has a Cubic crystal system#Bravais lattice, face centered cubic (fcc) arrangement of the atoms, although they are also known for other types of crystal structure. They nucleate at quite small sizes in the nanometer range, but can be grown much larger. They have been found in mineral crystals excavated from mines such as pentagonite or native gold from Ukraine, in rods of metals grown via electrochemical processes and in nanoparticles produced by the condensation of metals either onto substrates or in inert gases. They have been investigated for their potential uses in areas such as improving the efficiency of solar cell or heterogeneous catalysis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nucleation
In thermodynamics, nucleation is the first step in the formation of either a new Phase (matter), thermodynamic phase or Crystal structure, structure via self-assembly or self-organization within a substance or mixture. Nucleation is typically defined to be the process that determines how long an observer has to wait before the new phase or self-organized structure appears. For example, if a volume of water is cooled (at atmospheric pressure) significantly below 0°C, it will tend to Freezing, freeze into ice, but volumes of water cooled only a few degrees below 0°C often stay completely free of ice for long periods (supercooling). At these conditions, nucleation of ice is either slow or does not occur at all. However, at lower temperatures nucleation is fast, and ice crystals appear after little or no delay. Nucleation is a common mechanism which generates first-order phase transitions, and it is the start of the process of forming a new thermodynamic phase. In contrast, new phas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nanoparticle
A nanoparticle or ultrafine particle is a particle of matter 1 to 100 nanometres (nm) in diameter. The term is sometimes used for larger particles, up to 500 nm, or fibers and tubes that are less than 100 nm in only two directions. At the lowest range, metal particles smaller than 1 nm are usually called atom clusters instead. Nanoparticles are distinguished from microparticles (1-1000 μm), "fine particles" (sized between 100 and 2500 nm), and "coarse particles" (ranging from 2500 to 10,000 nm), because their smaller size drives very different physical or chemical properties, like colloidal properties and ultrafast optical effects or electric properties. Being more subject to the Brownian motion, they usually do not sediment, like colloid, colloidal particles that conversely are usually understood to range from 1 to 1000 nm. Being much smaller than the wavelengths of visible light (400-700 nm), nanoparticles cannot be seen with ordinary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frustum
In geometry, a ; (: frusta or frustums) is the portion of a polyhedron, solid (normally a pyramid (geometry), pyramid or a cone (geometry), cone) that lies between two parallel planes cutting the solid. In the case of a pyramid, the base faces are polygonal and the side faces are trapezoidal. A ''right frustum'' is a right pyramid or a right cone truncation (geometry), truncated perpendicularly to its axis; otherwise, it is an ''oblique frustum''. In a ''truncated cone'' or ''truncated pyramid'', the truncation plane is necessarily parallel to the cone's base, as in a frustum. If all its edges are forced to become of the same length, then a frustum becomes a ''Prism (geometry), prism'' (possibly oblique or/and with irregular bases). Elements, special cases, and related concepts A frustum's axis is that of the original cone or pyramid. A frustum is circular if it has circular bases; it is right if the axis is perpendicular to both bases, and oblique otherwise. The height of a f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George W
George Walker Bush (born July 6, 1946) is an American politician and businessman who was the 43rd president of the United States from 2001 to 2009. A member of the Bush family and the Republican Party (United States), Republican Party, he is the eldest son of the 41st president, George H. W. Bush, and was the 46th governor of Texas from 1995 to 2000. Bush flew warplanes in the Texas Air National Guard in his twenties. After graduating from Harvard Business School in 1975, he worked in the oil industry. He later co-owned the Major League Baseball team Texas Rangers (baseball), Texas Rangers before being elected governor of Texas 1994 Texas gubernatorial election, in 1994. Governorship of George W. Bush, As governor, Bush successfully sponsored legislation for tort reform, increased education funding, set higher standards for schools, and reformed the criminal justice system. He also helped make Texas the Wind power in Texas, leading producer of wind-generated electricity in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with seven faces, fifteen edges, and ten vertices. As a semiregular (or uniform) polyhedron If faces are all regular, the pentagonal prism is a semiregular polyhedron, more generally, a uniform polyhedron, and the third in an infinite set of prisms formed by square sides and two regular polygon caps. It can be seen as a '' truncated pentagonal hosohedron'', represented by Schläfli symbol t. Alternately it can be seen as the Cartesian product of a regular pentagon and a line segment, and represented by the product ×. The dual of a pentagonal prism is a pentagonal bipyramid. The symmetry group of a right pentagonal prism is ''D5h'' of order 20. The rotation group is ''D5'' of order 10. Volume The volume, as for all prisms, is the product of the area of the pentagonal base times the height or distance along any edge perpendicular to the base. For a uniform pentagonal prism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
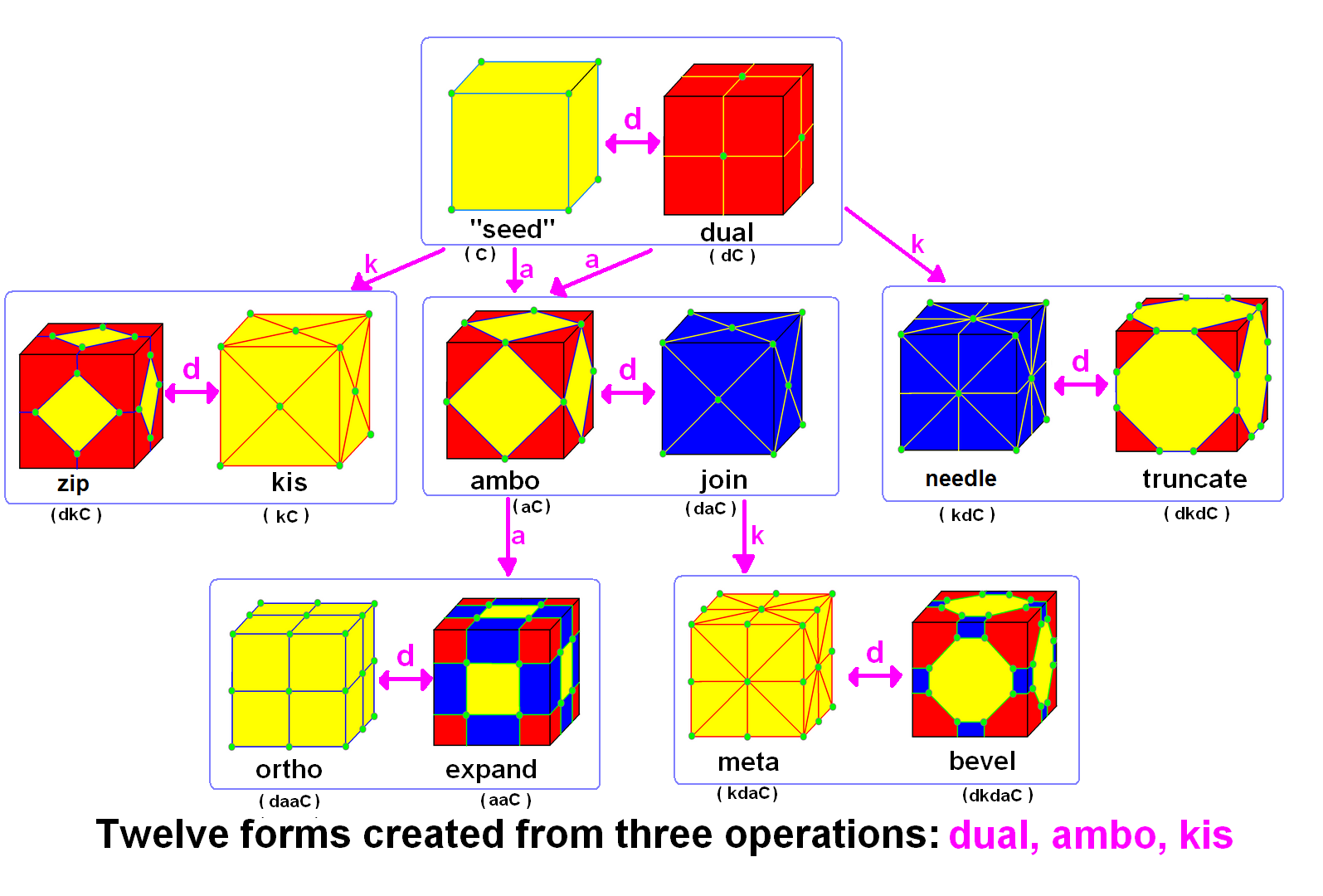
Conway Polyhedron Notation
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is ( topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), ( snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new Facet (geometry), facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids. Uniform truncation In general any polyhedron (or polytope) can also be truncated with a degree of freedom as to how deep the cut is, as shown in Conway polyhedron notation truncation operation. A special kind of truncation, usually implied, is a uniform truncation, a truncation operator applied to a regular polyhedron (or regular polytope) which creates a resulting uniform polyhedron (uniform polytope) with equal edge lengths. There are no degrees of freedom, and it represents a fixed geometric, just like the regular polyhedra. In general all single ringed uniform polytopes have a uniform truncation. For example, the icosidodecahedron, represented as Schläfli symbols r or \begin 5 \\ 3 \end, and Coxeter-Dynkin diagram or has a uniform truncation, the truncate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Bipyramid
In geometry, the elongated pentagonal bipyramid is a polyhedron constructed by attaching two pentagonal pyramids onto the base of a pentagonal prism. It is an example of Johnson solid. Construction The elongated pentagonal bipyramid is constructed from a pentagonal prism by attaching two pentagonal pyramids onto its bases, a process called elongation. These pyramids cover the pentagonal faces so that the resulting polyhedron ten equilateral triangles and five squares. A convex polyhedron in which all of the faces are regular polygons is the Johnson solid. The elongated pentagonal bipyramid is among them, enumerated as the sixteenth Johnson solid J_ . Properties The surface area of an elongated pentagonal bipyramid A is the sum of all polygonal faces' area: ten equilateral triangles, and five squares. Its volume V can be ascertained by dissecting it into two pentagonal pyramids and one regular pentagonal prism and then adding its volume. Given an elongated pentagonal bip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
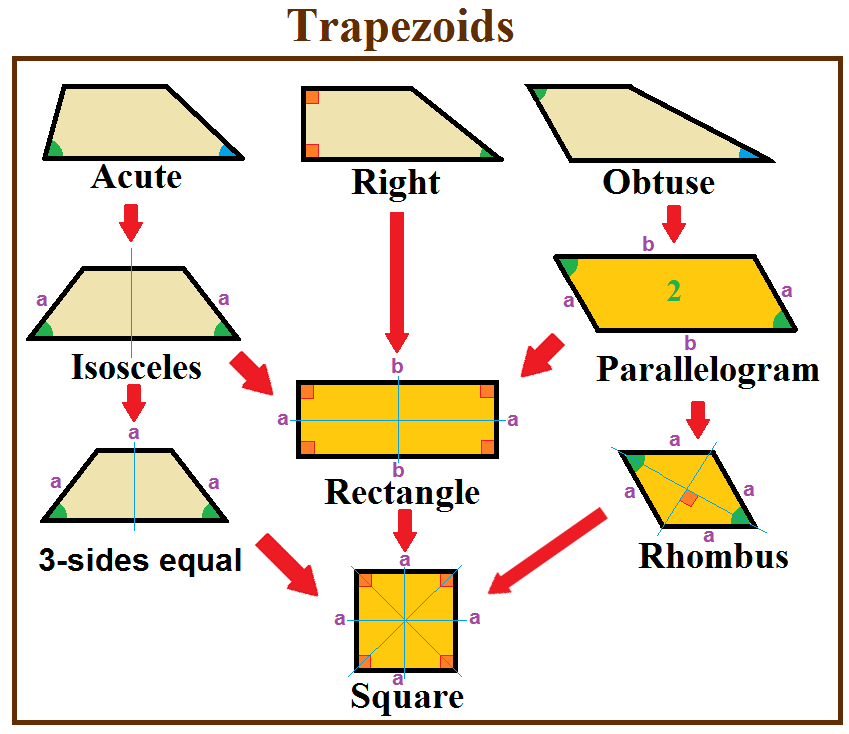
Trapezoid
In geometry, a trapezoid () in North American English, or trapezium () in British English, is a quadrilateral that has at least one pair of parallel sides. The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' or ''lateral sides''. (If the trapezoid is a parallelogram, then the choice of bases and legs is arbitrary.) A trapezoid is usually considered to be a convex quadrilateral in Euclidean geometry, but there are also crossed cases. If ''ABCD'' is a convex trapezoid, then ''ABDC'' is a crossed trapezoid. The metric formulas in this article apply in convex trapezoids. Definitions ''Trapezoid'' can be defined exclusively or inclusively. Under an exclusive definition a trapezoid is a quadrilateral having pair of parallel sides, with the other pair of opposite sides non-parallel. Parallelograms including rhombi, rectangles, and squares are then not considered to be trapezoids. Under an inclusive definition, a trapezoid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |