|
Pearson Type II Distribution
The Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics. History The Pearson system was originally devised in an effort to model visibly skewed observations. It was well known at the time how to adjust a theoretical model to fit the first two cumulants or moments of observed data: Any probability distribution can be extended straightforwardly to form a location-scale family. Except in pathological cases, a location-scale family can be made to fit the observed mean (first cumulant) and variance (second cumulant) arbitrarily well. However, it was not known how to construct probability distributions in which the skewness (standardized third cumulant) and kurtosis (standardized fourth cumulant) could be adjusted equally freely. This need became apparent when trying to fit known theoretical models to observed data that ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson System
Pearson may refer to: Organizations Education * Lester B. Pearson College, Victoria, British Columbia, Canada * Pearson College (UK), London, owned by Pearson PLC * Lester B. Pearson High School (other) Companies * Pearson plc, a UK-based international media conglomerate, best known as a book publisher ** Pearson Education, the textbook division of Pearson PLC *** Pearson-Longman, an imprint of Pearson Education * Pearson Yachts Places *Pearson, Georgia, a US city * Pearson, Texas, an unincorporated community in the US * Pearson, Victoria, a ghost town in Australia * Pearson, Wisconsin, an unincorporated community in the US *Toronto Pearson International Airport, in Toronto, Ontario, Canada * Pearson Field, in Vancouver, Washington, US * Pearson Island, an island in South Australia which is part of the Pearson Isles * Pearson Isles, an island group in South Australia Other uses * Pearson (surname) *Pearson correlation coefficient In statistics, the Pearson correlat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standardized Moment
In probability theory and statistics, a standardized moment of a probability distribution is a moment (often a higher degree central moment) that is normalized, typically by a power of the standard deviation, rendering the moment scale invariant. The shape of different probability distributions can be compared using standardized moments. Standard normalization Let be a random variable with a probability distribution and mean value \mu = \operatorname /math> (i.e. the first raw moment or moment about zero), the operator denoting the expected value of . Then the standardized moment of degree is that is, the ratio of the -th moment about the mean \mu_k = \operatorname \left ( X - \mu )^k \right = \int_^ ^k f(x)\,dx, to the -th power of the standard deviation, \sigma^k = \mu_2^ = \operatorname\!^. The power of is because moments scale as meaning that \mu_k(\lambda X) = \lambda^k \mu_k(X): they are homogeneous functions of degree , thus the standardized moment is sca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Mass Function
In probability and statistics, a probability mass function (sometimes called ''probability function'' or ''frequency function'') is a function that gives the probability that a discrete random variable is exactly equal to some value. Sometimes it is also known as the discrete probability density function. The probability mass function is often the primary means of defining a discrete probability distribution, and such functions exist for either scalar or multivariate random variables whose domain is discrete. A probability mass function differs from a continuous probability density function (PDF) in that the latter is associated with continuous rather than discrete random variables. A continuous PDF must be integrated over an interval to yield a probability. The value of the random variable having the largest probability mass is called the mode. Formal definition Probability mass function is the probability distribution of a discrete random variable, and provides the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. More precisely, the PDF is used to specify the probability of the random variable falling ''within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Prime Distribution
In probability theory and statistics, the beta prime distribution (also known as inverted beta distribution or beta distribution of the second kindJohnson et al (1995), p 248) is an absolutely continuous probability distribution. If p\in ,1/math> has a beta distribution, then the odds \frac has a beta prime distribution. Definitions Beta prime distribution is defined for x > 0 with two parameters ''α'' and ''β'', having the probability density function: : f(x) = \frac where ''B'' is the Beta function. The cumulative distribution function is : F(x; \alpha,\beta)=I_\left(\alpha, \beta \right) , where ''I'' is the regularized incomplete beta function. While the related beta distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed as a probability, the beta prime distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed in odds. The distribution is a Pearson type VI distribution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Sealy Gosset
William Sealy Gosset (13 June 1876 – 16 October 1937) was an English statistician, chemist and brewer who worked for Guinness. In statistics, he pioneered small sample experimental design. Gosset published under the pen name Student and developed Student's t-distribution – originally called Student's "z" – and "Student's test of statistical significance". Life and career Born in Canterbury, England, Canterbury, England the eldest son of Agnes Sealy Vidal and Colonel Frederic Gosset, R.E. Royal Engineers, Gosset attended Winchester College before matriculating as Winchester Scholar in natural sciences and mathematics at New College, Oxford. Upon graduating in 1899, he joined the brewery of Arthur Guinness & Son in Dublin, Ireland; he spent the rest of his 38-year career at Guinness. The site cites ''Dictionary of Scientific Biography'' (New York: Scribner's, 1972), pp. 476–477; ''International Encyclopedia of Statistics'', vol. I (New York: Free Press, 1978), pp. 409–4 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Student's T-distribution
In probability theory and statistics, Student's distribution (or simply the distribution) t_\nu is a continuous probability distribution that generalizes the Normal distribution#Standard normal distribution, standard normal distribution. Like the latter, it is symmetric around zero and bell-shaped. However, t_\nu has Heavy-tailed distribution, heavier tails, and the amount of probability mass in the tails is controlled by the parameter \nu. For \nu = 1 the Student's distribution t_\nu becomes the standard Cauchy distribution, which has very fat-tailed distribution, "fat" tails; whereas for \nu \to \infty it becomes the standard normal distribution \mathcal(0, 1), which has very "thin" tails. The name "Student" is a pseudonym used by William Sealy Gosset in his scientific paper publications during his work at the Guinness Brewery in Dublin, Ireland. The Student's distribution plays a role in a number of widely used statistical analyses, including Student's t- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
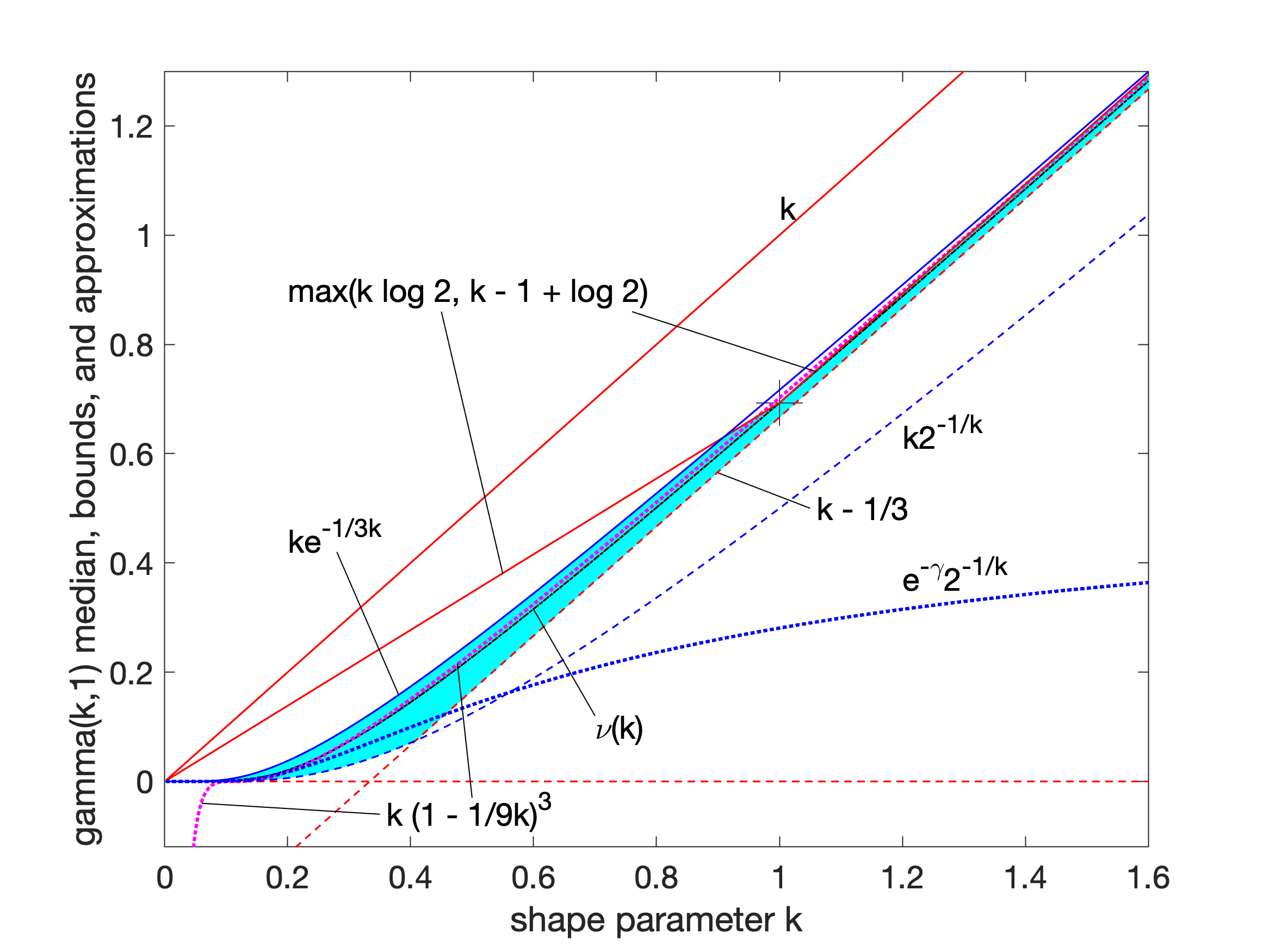
Gamma Distribution
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: # With a shape parameter and a scale parameter # With a shape parameter \alpha and a rate parameter In each of these forms, both parameters are positive real numbers. The distribution has important applications in various fields, including econometrics, Bayesian statistics, and life testing. In econometrics, the (''α'', ''θ'') parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer ''α'' values. Bayesian statisticians prefer the (''α'',''λ'') parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Probability
In probability theory, inverse probability is an old term for the probability distribution of an unobserved variable. Today, the problem of determining an unobserved variable (by whatever method) is called inferential statistics. The method of inverse probability (assigning a probability distribution to an unobserved variable) is called Bayesian probability, the distribution of data given the unobserved variable is the likelihood function (which does not by itself give a probability distribution for the parameter), and the distribution of an unobserved variable, given both data and a prior distribution, is the posterior distribution. The development of the field and terminology from "inverse probability" to "Bayesian probability" is described by . The term "inverse probability" appears in an 1837 paper of De Morgan, in reference to Laplace's method of probability (developed in a 1774 paper, which independently discovered and popularized Bayesian methods, and a 1812 book), th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Distribution
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli, is the discrete probability distribution of a random variable which takes the value 1 with probability p and the value 0 with probability q = 1-p. Less formally, it can be thought of as a model for the set of possible outcomes of any single experiment that asks a yes–no question. Such questions lead to outcome (probability), outcomes that are Boolean-valued function, Boolean-valued: a single bit whose value is success/yes and no, yes/Truth value, true/Binary code, one with probability ''p'' and failure/no/false (logic), false/Binary code, zero with probability ''q''. It can be used to represent a (possibly biased) coin toss where 1 and 0 would represent "heads" and "tails", respectively, and ''p'' would be the probability of the coin landing on heads (or vice versa where 1 would represent tails and ''p'' would be the probability of tails). In particular, unfair co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Posterior Distribution
The posterior probability is a type of conditional probability that results from updating the prior probability with information summarized by the likelihood via an application of Bayes' rule. From an epistemological perspective, the posterior probability contains everything there is to know about an uncertain proposition (such as a scientific hypothesis, or parameter values), given prior knowledge and a mathematical model describing the observations available at a particular time. After the arrival of new information, the current posterior probability may serve as the prior in another round of Bayesian updating. In the context of Bayesian statistics, the posterior probability distribution usually describes the epistemic uncertainty about statistical parameters conditional on a collection of observed data. From a given posterior distribution, various point and interval estimates can be derived, such as the maximum a posteriori (MAP) or the highest posterior density interval ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |