|
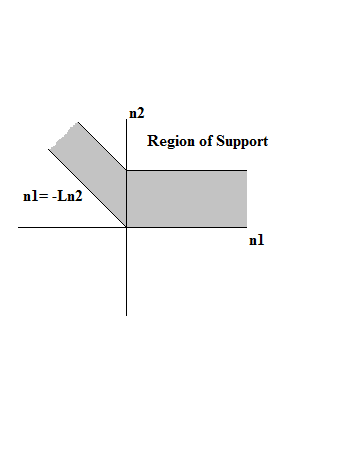
Papoulis-Marks-Cheung Approach
The Papoulis-Marks-Cheung approach is a theorem in multidimensional Shannon sampling theory that shows that the sampling density of a two-dimensional bandlimited function can be reduced to the support of the Fourier transform of the function. Applying a multidimensional generalization of a theorem by Athanasios Papoulis, the approach was first proposed by Robert J. Marks II and Kwang Fai Cheung. The approach has been called "elegant," "remarkably" closed, and "interesting." The Theorem The two-dimensional Fourier transform, or frequency spectrum, of a function f(x,y) is F(u_x,y_y) = \iint\limits_ f(x,y)^\operatorname\!x\operatorname\!ywhere u_x and u_x are the spatial frequencies corresponding to x and y. When x and y are lengths, spatial frequency has units of cycles per unit length. Prelee and Neuhoff describe the Papoulis-Marks-Cheung approach as follows. In deriving their result, Marks and Cheung relied on Papoulis' generalized sampling expansion. Explanation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Support (mathematics)
In mathematics, the support of a real-valued function f is the subset of the function domain containing the elements which are not mapped to zero. If the domain of f is a topological space, then the support of f is instead defined as the smallest closed set containing all points not mapped to zero. This concept is used very widely in mathematical analysis. Formulation Suppose that f : X \to \R is a real-valued function whose domain is an arbitrary set X. The of f, written \operatorname(f), is the set of points in X where f is non-zero: \operatorname(f) = \. The support of f is the smallest subset of X with the property that f is zero on the subset's complement. If f(x) = 0 for all but a finite number of points x \in X, then f is said to have . If the set X has an additional structure (for example, a topology), then the support of f is defined in an analogous way as the smallest subset of X of an appropriate type such that f vanishes in an appropriate sense on its compleme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Athanasios Papoulis
Athanasios Papoulis ( el, Αθανάσιος Παπούλης; 1921 – April 25, 2002) was a Greek-American engineer and applied mathematician. Life Papoulis was born in modern day Turkey in 1921, and his family was moved to Athens, Greece in 1922 as a consequence of the Population exchange between Greece and Turkey. He earned his undergraduate degree from National Technical University of Athens. In 1945, he stowed away on a boat to escape the impending Greek Civil War and settled in the United States. He studied under the supervision of John Robert Kline at the University of Pennsylvania and earned his Ph.D. in Mathematics in 1950. His dissertation was titled ''On the Strong Differentiation of the Indefinite Integral.'' He married Caryl Engwall in New York, New York in 1953, and had five children: Irene, Helen, James, Ann, and Mary. In 1952, after teaching briefly at Union College, he became a faculty member at the Polytechnic Institute of Brooklyn (now Polytechnic Institut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert J
The name Robert is an ancient Germanic given name, from Proto-Germanic "fame" and "bright" (''Hrōþiberhtaz''). Compare Old Dutch ''Robrecht'' and Old High German ''Hrodebert'' (a compound of '' Hruod'' ( non, Hróðr) "fame, glory, honour, praise, renown" and ''berht'' "bright, light, shining"). It is the second most frequently used given name of ancient Germanic origin. It is also in use as a surname. Another commonly used form of the name is Rupert. After becoming widely used in Continental Europe it entered England in its Old French form ''Robert'', where an Old English cognate form (''Hrēodbēorht'', ''Hrodberht'', ''Hrēodbēorð'', ''Hrœdbœrð'', ''Hrœdberð'', ''Hrōðberχtŕ'') had existed before the Norman Conquest. The feminine version is Roberta. The Italian, Portuguese, and Spanish form is Roberto. Robert is also a common name in many Germanic languages, including English, German, Dutch, Norwegian, Swedish, Scots, Danish, and Icelandic. It can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multidimensional Transform
In mathematical analysis and applications, multidimensional transforms are used to analyze the frequency content of signals in a domain of two or more dimensions. Multidimensional Fourier transform One of the more popular multidimensional transforms is the Fourier transform, which converts a signal from a time/space domain representation to a frequency domain representation.Smith, W. Handbook of Real-Time Fast Fourier Transforms:Algorithms to Product Testing, Wiley_IEEE Press, edition 1, pages 73–80, 1995 The discrete-domain multidimensional Fourier transform (FT) can be computed as follows: : F(w_1,w_2,\dots,w_m) = \sum_^\infty \sum_^\infty \cdots \sum_^\infty f(n_1,n_2,\dots,n_m) e^ where ''F'' stands for the multidimensional Fourier transform, ''m'' stands for multidimensional dimension. Define ''f'' as a multidimensional discrete-domain signal. The inverse multidimensional Fourier transform is given by : f(n_1,n_2,\dots,n_m) = \left(\frac\right ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multidimensional Sampling
In digital signal processing, multidimensional sampling is the process of converting a function of a multidimensional variable into a discrete collection of values of the function measured on a discrete set of points. This article presents the basic result due to Petersen and MiddletonD. P. Petersen and D. Middleton, "Sampling and Reconstruction of Wave-Number-Limited Functions in N-Dimensional Euclidean Spaces", Information and Control, vol. 5, pp. 279–323, 1962. on conditions for perfectly reconstructing a wavenumber-limited function from its measurements on a discrete lattice of points. This result, also known as the Petersen–Middleton theorem, is a generalization of the Nyquist–Shannon sampling theorem for sampling one-dimensional band-limited functions to higher-dimensional Euclidean spaces. In essence, the Petersen–Middleton theorem shows that a wavenumber-limited function can be perfectly reconstructed from its values on an infinite lattice of points, provided the l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aliasing
In signal processing and related disciplines, aliasing is an effect that causes different signals to become indistinguishable (or ''aliases'' of one another) when sampled. It also often refers to the distortion or artifact that results when a signal reconstructed from samples is different from the original continuous signal. Aliasing can occur in signals sampled in time, for instance digital audio, or the stroboscopic effect, and is referred to as temporal aliasing. It can also occur in spatially sampled signals (e.g. moiré patterns in digital images); this type of aliasing is called spatial aliasing. Aliasing is generally avoided by applying low-pass filters or anti-aliasing filters (AAF) to the input signal before sampling and when converting a signal from a higher to a lower sampling rate. Suitable reconstruction filtering should then be used when restoring the sampled signal to the continuous domain or converting a signal from a lower to a higher sampling rate. F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Rate
In signal processing, the Nyquist rate, named after Harry Nyquist, is a value (in units of samples per second or hertz, Hz) equal to twice the highest frequency ( bandwidth) of a given function or signal. When the function is digitized at a higher sample rate (see ), the resulting discrete-time sequence is said to be free of the distortion known as aliasing. Conversely, for a given sample-rate the corresponding Nyquist frequency in Hz is one-half the sample-rate. Note that the ''Nyquist rate'' is a property of a continuous-time signal, whereas ''Nyquist frequency'' is a property of a discrete-time system. The term ''Nyquist rate'' is also used in a different context with units of symbols per second, which is actually the field in which Harry Nyquist was working. In that context it is an upper bound for the symbol rate across a bandwidth-limited baseband channel such as a telegraph line or passband channel such as a limited radio frequency band or a frequency division m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |