|
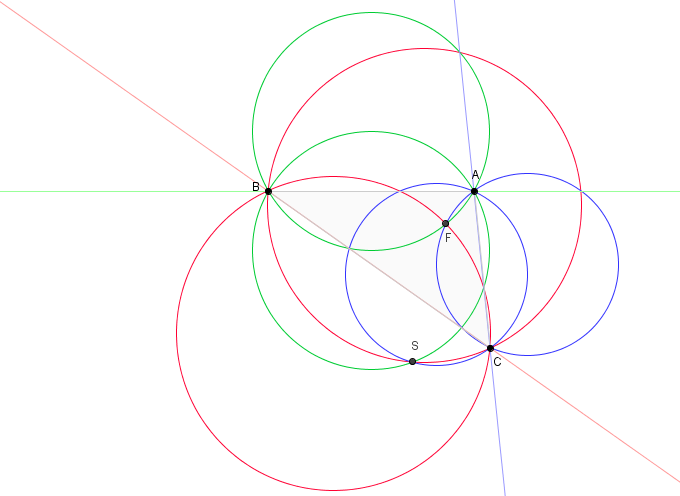
Orthocentroidal Disk
In geometry, the orthocentroidal circle of a non-equilateral triangle is the circle that has the triangle's orthocenter and centroid at opposite ends of its diameter. This diameter also contains the triangle's nine-point center and is a subset of the Euler line, which also contains the circumcenter outside the orthocentroidal circle. Andrew Guinand showed in 1984 that the triangle's incenter must lie in the interior of the orthocentroidal circle, but not coinciding with the nine-point center; that is, it must fall in the open orthocentroidal disk punctured at the nine-point center... . The incenter could be any such point, depending on the specific triangle having that particular orthocentroidal disk. Furthermore, the Fermat point, the Gergonne point, and the symmedian point are in the open orthocentroidal disk punctured at its own center (and could be at any point therein), while the second Fermat point and Feuerbach point are in the exterior of the orthocentroidal ci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Mathematical Monthly
''The American Mathematical Monthly'' is a peer-reviewed scientific journal of mathematics. It was established by Benjamin Finkel in 1894 and is published by Taylor & Francis on behalf of the Mathematical Association of America. It is an expository journal intended for a wide audience of mathematicians, from undergraduate students to research professionals. Articles are chosen on the basis of their broad interest and reviewed and edited for quality of exposition as well as content. The editor-in-chief An editor-in-chief (EIC), also known as lead editor or chief editor, is a publication's editorial leader who has final responsibility for its operations and policies. The editor-in-chief heads all departments of the organization and is held accoun ... is Vadim Ponomarenko ( San Diego State University). The journal gives the Lester R. Ford Award annually to "authors of articles of expository excellence" published in the journal. Editors-in-chief The following persons are or have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brocard Points
In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard (1845–1922), a French mathematician. Definition In a triangle with sides , where the vertices are labeled in counterclockwise order, there is exactly one point such that the line segments form the same angle, , with the respective sides , namely that \angle PAB = \angle PBC = \angle PCA =\omega.\, Point is called the first Brocard point of the triangle , and the angle is called the Brocard angle of the triangle. This angle has the property that \cot\omega = \cot\!\bigl(\angle CAB\bigr) + \cot\!\bigl(\angle ABC\bigr) + \cot\!\bigl(\angle BCA\bigr). There is also a second Brocard point, , in triangle such that line segments form equal angles with sides respectively. In other words, the equations \angle QCB = \angle QBA = \angle QAC apply. Remarkably, this second Brocard point has the same Brocard angle as the first Brocard point. In other words, angle \angle PBC = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locus (mathematics)
In geometry, a locus (plural: ''loci'') (Latin word for "place", "location") is a set (mathematics), set of all Point (geometry), points (commonly, a line (geometry), line, a line segment, a curve (mathematics), curve or a Surface (topology), surface), whose location satisfies or is determined by one or more specified conditions.. The set of the points that satisfy some property is often called the ''locus of a point'' satisfying this property. The use of the singular in this formulation is a witness that, until the end of the 19th century, mathematicians did not consider infinite sets. Instead of viewing lines and curves as sets of points, they viewed them as places where a point may be ''located'' or may move. History and philosophy Until the beginning of the 20th century, a geometrical shape (for example a curve) was not considered as an infinite set of points; rather, it was considered as an entity on which a point may be located or on which it moves. Thus a circle (mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feuerbach Point
In the geometry of triangles, the incircle and nine-point circle of a triangle are internally tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is a triangle center, meaning that its definition does not depend on the placement and scale of the triangle. It is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers, and is named after Karl Wilhelm Feuerbach..Encyclopedia of Triangle Centers , accessed 2014-10-24. Feuerbach's theorem, published by Feuerbach in 1822, states more generally that the nine-point circle is tangent to the three s of the triangle as well as its incircle. A very short proof of this theorem based on [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmedian Point
In geometry, symmedians are three particular lines associated with every triangle. They are constructed by taking a median of the triangle (a line connecting a vertex with the midpoint of the opposite side), and reflecting the line over the corresponding angle bisector (the line through the same vertex that divides the angle there in half). The angle formed by the symmedian and the angle bisector has the same measure as the angle between the median and the angle bisector, but it is on the other side of the angle bisector. The three symmedians meet at a triangle center called the Lemoine point. Ross Honsberger has called its existence "one of the crown jewels of modern geometry".. Isogonality Many times in geometry, if we take three special lines through the vertices of a triangle, or '' cevians'', then their reflections about the corresponding angle bisectors, called ''isogonal lines'', will also have interesting properties. For instance, if three cevians of a triangle inters ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gergonne Point
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter. An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides. The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex , for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex , or the excenter of . Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat Point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible or, equivalently, the geometric median of the three vertices. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it. The Fermat point gives a solution to the geometric median and Steiner tree problems for three points. Construction The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows: # Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle. # Draw a line from each new vertex to the opposite vertex of the original triangle. # The two lines intersect at the Fermat point. An alternative method is the following: # On each of two ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Gazette
''The Mathematical Gazette'' is a triannual peer-reviewed academic journal published by Cambridge University Press on behalf of the Mathematical Association. It covers mathematics education with a focus on the 15–20 years age range. The journal was established in 1894 by Edward Mann Langley as the successor to the ''Reports of the Association for the Improvement of Geometrical Teaching''. William John Greenstreet was its editor-in-chief for more than thirty years (1897–1930). Since 2000, the editor is Gerry Leversha. Editors-in-chief The following persons are or have been editor-in-chief: Abstracting and indexing The journal is abstracted and indexed in EBSCO databases, Emerging Sources Citation Index, Scopus Scopus is a scientific abstract and citation database, launched by the academic publisher Elsevier as a competitor to older Web of Science in 2004. The ensuing competition between the two databases has been characterized as "intense" and is c ..., and zbMA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forum Geometricorum
''Forum Geometricorum: A Journal on Classical Euclidean Geometry'' was a peer-reviewed open-access academic journal that specialized in mathematical research papers on Euclidean geometry. Founded in 2001, it was published by Florida Atlantic University and was indexed by Mathematical Reviews ''Mathematical Reviews'' is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also pu ... and .. Its founding editor-in-chief was Paul Yiu, a professor of mathematics at Florida Atlantic. In 2019, Forum Geometricorum published what was later announced to be its final issue, and stopped accepting submissions, after the retirement of Yiu. Prior issues are still available. Volumes for 2001 to 2009 can be accessed as a single searchable file (see below). Individual articles up to 2019 are available from Internet Archive (see below). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incenter
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle. Together with the centroid, circumcenter, and orthocenter, it is one of the four triangle centers known to the ancient Greeks, and the only one of the four that does not in general lie on the Euler line. It is the first listed center, X(1), in Clark Kimberling's Encyclopedia of Triangle Centers, and the identity element of the multiplicative group of triangle centers.. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |