|
Orbital State Vectors
In astrodynamics and celestial dynamics, the orbital state vectors (sometimes state vectors) of an orbit are cartesian coordinate system, Cartesian vectors of position (vector), position (\mathbf) and velocity (\mathbf) that together with their time (epoch (astronomy), epoch) (t) uniquely determine the trajectory of the orbiting body in space. Orbital state vectors come in many forms including the traditional Position-Velocity vectors, Two-line element set (TLE), and Vector Covariance Matrix (VCM). Frame of reference State vectors are defined with respect to some frame of reference, usually but not always an inertial reference frame. One of the more popular reference frames for the state vectors of bodies moving near Earth is the Earth-centered inertial (ECI) system defined as follows: *The origin (geometry), origin is Earth's center of mass; *The Z axis is coincident with Earth's rotational axis, positive northward; *The X/Y plane coincides with Earth's equatorial plane, with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axial Precession (astronomy)
In astronomy, axial precession is a gravity-induced, slow, and continuous change in the orientation of an astronomical body's rotational axis. In the absence of precession, the astronomical body's orbit would show axial parallelism. In particular, axial precession can refer to the gradual shift in the orientation of Earth's axis of rotation in a cycle of approximately 26,000 years.Hohenkerk, C.Y., Yallop, B.D., Smith, C.A., & Sinclair, A.T. "Celestial Reference Systems" in Seidelmann, P.K. (ed.) ''Explanatory Supplement to the Astronomical Almanac''. Sausalito: University Science Books. p. 99. This is similar to the precession of a spinning top, with the axis tracing out a pair of cones joined at their apices. The term "precession" typically refers only to this largest part of the motion; other changes in the alignment of Earth's axis— nutation and polar motion—are much smaller in magnitude. Earth's precession was historically called the precession of the equinoxes, b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiation (mathematics)
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leibn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Vector
In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat"). The term ''normalized vector'' is sometimes used as a synonym for ''unit vector''. The normalized vector û of a non-zero vector u is the unit vector in the direction of u, i.e., :\mathbf = \frac=(\frac, \frac, ... , \frac) where ‖u‖ is the Norm (mathematics), norm (or length) of u and \, \mathbf\, = (u_1, u_2, ..., u_n). The proof is the following: \, \mathbf\, =\sqrt=\sqrt=\sqrt=1 A unit vector is often used to represent direction (geometry), directions, such as normal directions. Unit vectors are often chosen to form the basis (linear algebra), basis of a vector space, and every vector in the space may be written as a linear combination form of unit vectors. Orthogonal coordinates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve at a point if the line passes through the point on the curve and has slope , where ''f'' is the derivative of ''f''. A similar definition applies to space curves and curves in ''n''-dimensional Euclidean space. The point where the tangent line and the curve meet or intersect is called the ''point of tangency''. The tangent line is said to be "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. The tangent line to a point on a differentiable curve can also be thought of as a '' tangent line approximation'', the graph of the affine function that best approximates the original function at the given point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Suborbital
A sub-orbital spaceflight is a spaceflight in which the spacecraft reaches outer space, but its trajectory intersects the surface of the gravitating body from which it was launched. Hence, it will not complete one orbital revolution, will not become an artificial satellite nor will it reach escape velocity. For example, the path of an object launched from Earth that reaches the Kármán line (about – above sea level), and then falls back to Earth, is considered a sub-orbital spaceflight. Some sub-orbital flights have been undertaken to test spacecraft and launch vehicles later intended for orbital spaceflight. Other vehicles are specifically designed only for sub-orbital flight; examples include crewed vehicles, such as the X-15 and SpaceShipTwo, and uncrewed ones, such as ICBMs and sounding rockets. Flights which attain sufficient velocity to go into low Earth orbit, and then de-orbit before completing their first full orbit, are not considered sub-orbital. Examples o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ballistically
Ballistics is the field of mechanics concerned with the launching, flight behaviour and impact effects of projectiles, especially weapon munitions such as bullets, unguided bombs, rockets and the like; the science or art of designing and accelerating projectiles so as to achieve a desired performance. A ballistic body is a free-moving body with momentum, which can be subject to forces such as those exerted by pressurized gases from a gun barrel or a propelling nozzle, normal force by rifling, and gravity and air drag during flight. A ballistic missile is a missile that is guided only during the relatively brief initial phase of powered flight, with the trajectory subsequently governed by the laws of classical mechanics, in contrast to (for example) a cruise missile, which is aerodynamically guided in powered flight like a fixed-wing aircraft. History and prehistory The earliest known ballistic projectiles were stones, spears, and the throwing stick. The oldest evidence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
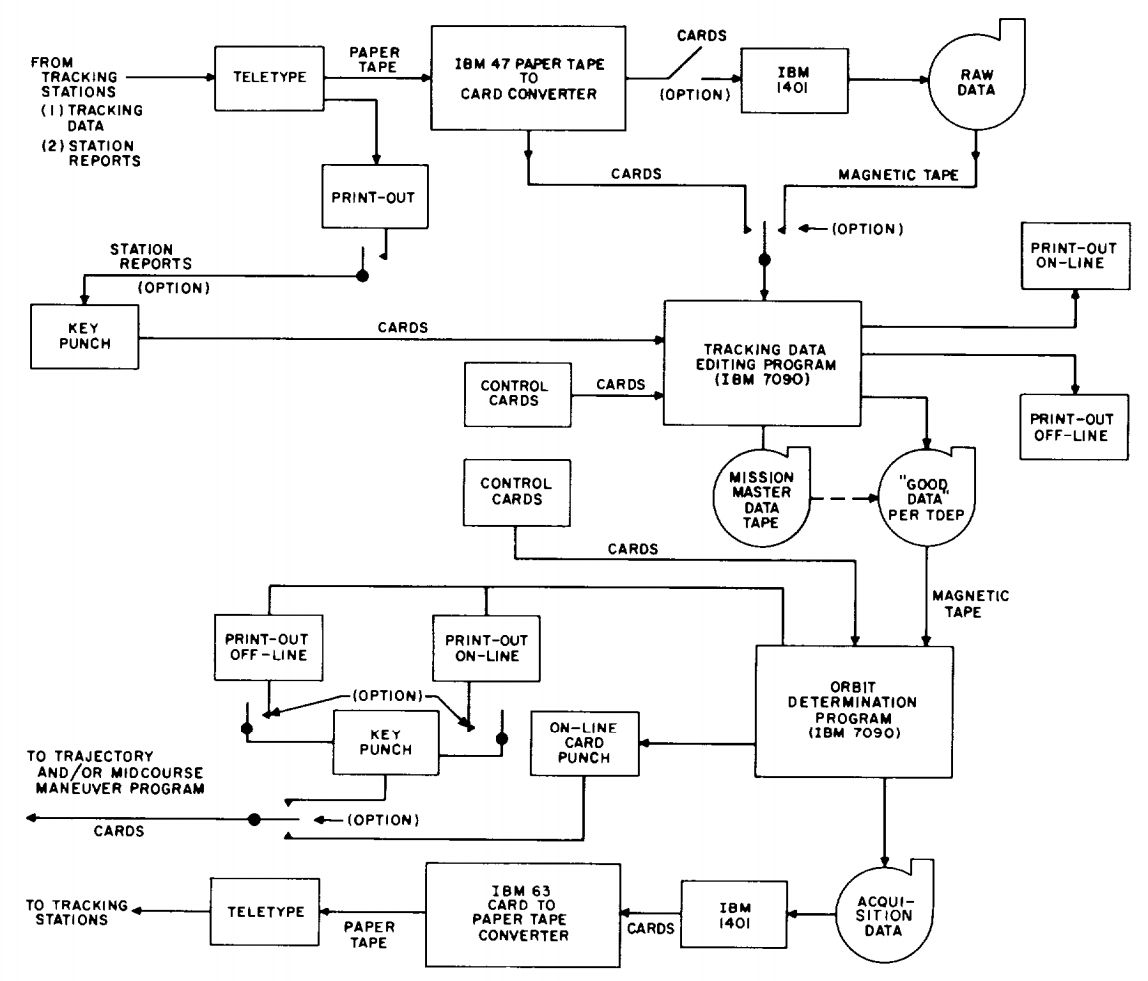
Orbit Determination
Orbit determination is the estimation of orbits of objects such as moons, planets, and spacecraft. One major application is to allow tracking newly observed asteroids and verify that they have not been previously discovered. The basic methods were discovered in the 17th century and have been continuously refined. ''Observations'' are the raw data fed into orbit determination algorithms. Observations made by a ground-based observer typically consist of time-tagged azimuth, elevation, range, and/or range rate values. Telescopes or radar apparatus are used, because naked-eye observations are inadequate for precise orbit determination. With more or better observations, the accuracy of the orbit determination process also improves, and fewer "false alarms" result. After orbits are determined, mathematical propagation techniques can be used to predict the future positions of orbiting objects. As time goes by, the actual path of an orbiting object tends to diverge from the predicte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Velocity Vector
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector quantity, meaning that both magnitude and direction are needed to define it. The scalar absolute value ( magnitude) of velocity is called , being a coherent derived unit whose quantity is measured in the SI (metric system) as metres per second (m/s or m⋅s−1). For example, "5 metres per second" is a scalar, whereas "5 metres per second east" is a vector. If there is a change in speed, direction or both, then the object is said to be undergoing an ''acceleration''. Definition Average velocity The average velocity of an object over a period of time is its change in position, \Delta s, divided by the duration of the period, \Delta t, given mathematically as\bar=\frac. Instantaneous velocity The instantaneous velocity of an object is the limit average velo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frame Of Reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system, whose origin (mathematics), origin, orientation (geometry), orientation, and scale (geometry), scale have been specified in physical space. It is based on a set of reference points, defined as point (geometry), geometric points whose position (geometry), position is identified both mathematically (with numerical coordinate values) and physically (signaled by conventional markers). An important special case is that of ''inertial reference frames'', a stationary or uniformly moving frame. For ''n'' dimensions, reference points are sufficient to fully define a reference frame. Using Cartesian coordinate system, rectangular Cartesian coordinates, a reference frame may be defined with a reference point at the origin and a reference point at one unit distance along each of the ''n'' coordinate Cartesian coordinate system, axes. In Theory of relativity, Einsteinian relativity, referen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position Vector
In geometry, a position or position vector, also known as location vector or radius vector, is a Euclidean vector that represents a point ''P'' in space. Its length represents the distance in relation to an arbitrary reference origin ''O'', and its direction represents the angular orientation with respect to given reference axes. Usually denoted x, r, or s, it corresponds to the straight line segment from ''O'' to ''P''. In other words, it is the displacement or translation that maps the origin to ''P'': :\mathbf=\overrightarrow. The term position vector is used mostly in the fields of differential geometry, mechanics and occasionally vector calculus. Frequently this is used in two-dimensional or three-dimensional space, but can be easily generalized to Euclidean spaces and affine spaces of any dimension.Keller, F. J., Gettys, W. E. et al. (1993), p. 28–29. Relative position The relative position of a point ''Q'' with respect to point ''P'' is the Euclidean vector res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-major Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |