|
Orbital Angular Momentum Of Free Electrons
Orbital may refer to: Sciences Chemistry and physics * Atomic orbital * Molecular orbital * Hybrid orbital Astronomy and space flight * Orbit ** Earth orbit Medicine and physiology * Orbit (anatomy), also known as the ''orbital bone'' * Orbitofrontal cortex, a part of the brain used for decision making Business * Orbital Corporation, an Australian engine technology company * Orbital Sciences Corporation, a U.S. satellite launch and defense systems corporation * Orbital ATK, American aerospace manufacturer formed from the merger of Orbital Sciences Corporation and parts of Alliant Techsystems Transportation * Ring road (or ''orbital road'' in some regions) * Orbital (metro), a rapid transit line usually encircling a city centre * Orbital engine Other uses * ''Orbital'' (novel), a 2023 novel by Samantha Harvey * Orbital (The Culture), artificial worlds from Iain M. Banks's series of science fiction novels, the Culture * Orbital (band), an English electronic dance music duo, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Orbital
In quantum mechanics, an atomic orbital () is a Function (mathematics), function describing the location and Matter wave, wave-like behavior of an electron in an atom. This function describes an electron's Charge density, charge distribution around the Atomic nucleus, atom's nucleus, and can be used to calculate the probability of finding an electron in a specific region around the nucleus. Each orbital in an atom is characterized by a set of values of three quantum numbers , , and , which respectively correspond to electron's energy, its angular momentum, orbital angular momentum, and its orbital angular momentum projected along a chosen axis (magnetic quantum number). The orbitals with a well-defined magnetic quantum number are generally complex-valued. Real-valued orbitals can be formed as linear combinations of and orbitals, and are often labeled using associated Spherical harmonics#Harmonic polynomial representation, harmonic polynomials (e.g., ''xy'', ) which describe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital (metro)
A circle route (also circumference, loop, ring route, ring line or orbital line) is a public transport route following a path approximating a circle or at least a closed curve. Definition The expression "circle route" may refer in particular to: * a route orbiting a central point, commonly the central business district (CBD) in a city or large town * a route running in approximately a circular path from a point near the centre of a city or town out to a peripheral point and back again * a feeder route running from an interchange station around a neighbourhood or suburb in approximately a circle Typical characteristics Typically, a circle route will connect at several locations with one or more cross-city routes or radial routes offering services in a straighter line into or out of a city or town centre. When a circle route orbits a central business district in a large arc, it will often provide transverse (or lateral) links between suburbs or satellites, either on its own or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital (comics)
Orbital is a Franco-Belgian science fiction comics series written by Sylvain Runberg, illustrated by Serge Pellé and published by Dupuis in French, Cinebook Cinebook Ltd is a British publishing company that publishes comic albums and graphic novels. It describes itself as "the 9th art publisher," the 9th art being comics in continental Europe, especially France, Belgium and Italy. They typically tr ... in English, Cobolt förlag in Swedish, in German and ReNoir Comics in Italy. Story The story follows a pair of Interworld Diplomatic Office (IDO) agents on their intergalactic diplomatic peace missions. The agents are Mezoke Izzua, a Sandjarrian, and Caleb Swany, a Human. The missions reveal a rich universe of various interwoven plots by various political and interest factions involving numerous cultures and races across the galaxy. Volumes # Cicatrices - April 2006 # Ruptures - June 2007 # Nomades - August 2009 # Ravages - October 2010 # Justice - September 2012 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital (1993 Album)
''Orbital'' (also known as ''Orbital 2'' or the Brown Album) is the second studio album by English electronic music duo Orbital, released on 24 May 1993 by Internal and FFRR Records. Like the duo's debut album, the album was officially untitled. The album peaked at number 28 on the UK Albums Chart. Album The album begins with "Time Becomes", which uses the same speech sample by the actor Michael Dorn in '' Star Trek: The Next Generation'' (Time squared - season 2 episode 13, Worf - 20'30 : "There is the theory of the Möbius. A twist in the fabric of space where time becomes a loop") which opened their first album. The piece uses phasing, a technique popularised by Steve Reich, in which two identical samples are repeated at slightly different speeds. The brothers enjoy aural puns, and the use of this sample again, as well as the muffled intro on "Planet of the Shapes" with intentional addition of record static and crackles, followed by the sound of a needle skipping grooves ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital (1991 Album)
''Orbital'' (also known as ''Orbital 1'' or the Green Album) is the debut studio album by English electronic music duo Orbital, released on 30 September 1991 by FFRR Records FFRR Records (sometimes credited as Full Frequency Range Recordings) is a dance music label founded as a subsidiary of London Records in 1986, with A&R run by the British DJ Pete Tong. Originally a part of London Records' label roster, F .... Orbital self-titled their first two albums so the "Green Album" is an unofficial name to distinguish it from the second album. The ''Mutations EP'' refers to the album as ''L.P. C.D. M.C.'', thus titling the album after the "LP" / "CD" / "MC" on the front cover of the respective format. Background Orbital was formed in the late 80s, and consisted of brothers Phil and Paul Hartnoll. Their first track, "Chime", was released in 1989 to much success, reaching #17 on the UK charts. They were signed to FFRR Records after a bidding war for the track, and the grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital (band)
Orbital are an English electronic music duo from Dunton Green, Kent, England, consisting of brothers Phil and Paul Hartnoll. The band's name is taken from Greater London's orbital motorway, the M25 motorway, M25, which was central to the early rave scene during the early days of acid house. Additionally, the cover art on three of their albums showcase stylised atomic orbitals. Orbital have been critically and commercially successful, known particularly for their live improvisation during shows. Career Early years and influences Paul Hartnoll described the early incarnation of Orbital as a "low-cost bedroom New Order (band), New Order/Severed Heads". Other influences from the late 1970s and early 1980s included The Beat (British band), The Beat, Cabaret Voltaire (band), Cabaret Voltaire, Orchestral Manoeuvres in the Dark, OMD and Kate Bush. The catalogues of Motown, Tamla Motown, ZTT Records, ZTT and Trojan Records, and the classic rock of bands like Deep Purple, Led Zeppelin a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital (The Culture)
The Culture is a fictional interstellar post-scarcity civilisation or society created by the Scottish writer Iain Banks and features in a number of his space opera novels and works of short fiction, collectively called the ''Culture'' series. In the series, the Culture is composed primarily of sentient beings of the humanoid alien variety, artificially intelligent sentient machines, and a small number of other sentient "alien" life forms. Machine intelligences range from human-equivalent drones to hyper-intelligent Minds. Artificial intelligences with capabilities measured as a fraction of human intelligence also perform a variety of tasks, e.g. controlling spacesuits. Without scarcity, the Culture has no need for money; instead, Minds voluntarily indulge humanoid and drone citizens' pleasures, leading to a largely hedonistic society. Many of the series' protagonists are humanoids who have chosen to work for the Culture's diplomatic or espionage organs, and interact with othe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital (novel)
''Orbital'' is a 2023 novel by English writer Samantha Harvey that incorporates elements of science fiction, literary fiction, and philosophical drama, published by Jonathan Cape in the UK and by Grove Atlantic in the US. It follows six fictional astronauts over 24 hours on an orbiting space station. The novel received positive reviews. It won the 2024 Booker Prize and the Hawthornden Prize, and it was shortlisted for the Orwell Prize for Political Fiction and the Ursula K. Le Guin Prize for imaginative fiction. Background Harvey watched a continuous live stream of Earth from the International Space Station while writing the novel. She started work on it in the 2010s but stopped writing after about 5,000 words because she felt her limited knowledge of the complex subject of space travel was inadequate to the task. As she told a BBC interviewer, "I thought, 'Well, I have never been to space. I could never go to space... Who am I to do this?'" In time, however, she stopped worr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Engine
The Sarich orbital engine is a type of internal combustion engine, invented in 1972 by Ralph Sarich, an engineer from Perth, Australia, which features orbital rather than reciprocating motion of its central piston. It differs from the conceptually similar Wankel engine by using a generally prismatic shaped piston that orbits the axis of the engine, without rotation, rather than the rotating trilobular rotor of the Wankel. Overview The engine promised to be about one third the size and weight of conventional piston engines due to the compact arrangement of the combustion chambers. Another advantage is that there is no high-speed contact area with the engine walls, unlike in the Wankel engine in which edge wear is a problem. However, the combustion chambers are divided by vanes which do have contact with both the walls and the orbiting piston and are more difficult to seal due to the eight corners of the combustion chamber. In the patent, the engine is described as two stroke in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ring Road
A ring road (also known as circular road, beltline, beltway, circumferential (high)way, loop or orbital) is a road or a series of connected roads encircling a town, city or country. The most common purpose of a ring road is to assist in reducing traffic volumes in the urban centre, such as by offering an alternate route around the city for drivers who do not need to stop in the city core. Ring roads can also serve to connect suburbs to each other, allowing efficient travel between them. Nomenclature The name "ring road" is used for the majority of metropolitan circumferential routes in Europe, such as the Berliner Ring, the Brussels Ring, the Amsterdam Ring and the Leeds Inner and Outer ring roads. Australia, Pakistan, and India also use the term ring road, as in Melbourne's Western Ring Road, Lahore's Lahore Ring Road and Hyderabad's Outer Ring Road. In Canada the term is the most commonly used, with "orbital" also used, but to a much lesser extent. In Europe and Aust ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
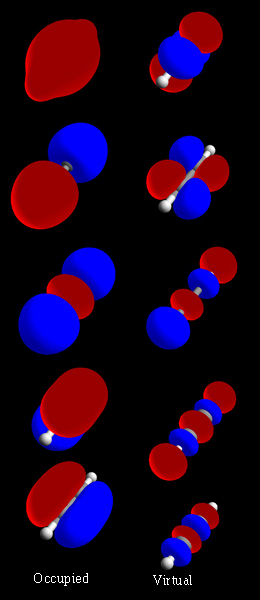
Molecular Orbital
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms ''atomic orbital'' and ''molecular orbital'' were introduced by Robert S. Mulliken in 1932 to mean ''one-electron orbital wave functions''. At an elementary level, they are used to describe the ''region'' of space in which a function has a significant amplitude. In an isolated atom, the orbital electrons' location is determined by functions called atomic orbitals. When multiple atoms combine chemically into a molecule by forming a valence chemical bond, the electrons' locations are determined by the molecule as a whole, so the atomic orbitals combine to form molecular orbitals. The electrons from the constituent atoms occupy the molecular orbitals. Mathematically, molecular orbitals are an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital ATK
Orbital ATK Inc. was an American aerospace manufacturer and defense industry company. It was formed in February 9, 2015 from the merger of Orbital Sciences Corporation and parts of Alliant Techsystems (ATK). Orbital ATK designed, built, and delivered rocket engines, military vehicles, firearms, autocannons, missiles, ammunition, precision-guided munitions, satellites, missile approach warning systems, launch vehicles and spacecraft. The company was acquired by Northrop Grumman on June 6, 2018. The former Orbital ATK operations were renamed Northrop Grumman Innovation Systems and operated as a division until January 1, 2020 when a reorganization merged the operations into the company's other divisions. History A merger of Orbital Sciences Corporation and the defense and aerospace divisions of Alliant Techsystems (ATK) was announced on April 29, 2014. The two companies had collaborated on several previous projects, including the use of 400 ATK rocket motors in Orbital's laun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |