|
Nyquist Stability Criterion
In control theory and stability theory, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer at Siemens in 1930 and the Swedish-American electrical engineer Harry Nyquist at Bell Telephone Laboratories in 1932, is a graphical technique for determining the stability criterion, stability of a linear dynamical system. Because it only looks at the Nyquist plot of the Open-loop controller, open loop systems, it can be applied without explicitly computing the poles and zeros of either the closed-loop or open-loop system (although the number of each type of right-half-plane Singularity (mathematics), singularities must be known). As a result, it can be applied to systems defined by non-rational functions, such as systems with delays. In contrast to Bode plots, it can handle transfer functions with right half-plane singularities. In addition, there is a natural generalization to more complex systems with M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Example
Nyquist may refer to: *Nyquist (surname) *Nyquist (horse), winner of the 2016 Kentucky Derby *Nyquist (programming language), computer programming language for sound synthesis and music composition See also *Johnson–Nyquist noise, thermal noise *Nyquist stability criterion, in control theory **Nyquist plot, signal processing and electronic feedback *Nyquist–Shannon sampling theorem, fundamental result in the field of information theory **Nyquist frequency, digital signal processing **Nyquist rate, telecommunication theory **Nyquist ISI criterion, telecommunication theory *6625 Nyquist, a main-belt asteroid *Nyquist filter, a filter used in television systems *Enquist *Nyqvist (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feedback
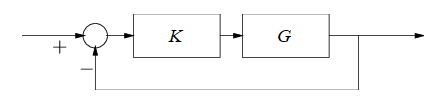
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause and effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled carefully when applied to feedback systems: History Self-regulating mechanisms have existed since antiquity, and the idea of feedback started to enter economic theory in Britain by the 18th century, but it was not at that time recognized as a universal abstraction and so did not have a name. The first ever known artificial feedback device was a float valve, for maintaining water at a constant level, invented in 270 BC in Alexandria, Egypt. This device illustrated the principle of feedback: a low water level opens the valve, the rising water then provides feedback into the system, closing the valve when the required level is reached. This then reoccurs in a circular fashion as the water level fluctuates. Centrifugal governors were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular oriented lines, called '' coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the '' origin'' and has as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any dimension . These coordinates are the signed distances from the point to mutually perpendicular fixed h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Systems
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial control systems which are used for controlling Process (engineering), processes or machines. The control systems are designed via control engineering process. For continuously modulated control, a feedback controller is used to automatically control a process or operation. The control system compares the value or status of the process variable (PV) being controlled with the desired value or Setpoint (control system), setpoint (SP), and applies the difference as a control signal to bring the process variable output of the Plant (control theory), plant to the same value as the setpoint. For Sequential logic, sequential and combinational logic, software logic, such as in a programmable logic controller, is used. Open-loop and closed-loop co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Plot
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point, as functions of one or several variables called parameters. In the case of a single parameter, parametric equations are commonly used to express the trajectory of a moving point, in which case, the parameter is often, but not necessarily, time, and the point describes a curve, called a parametric curve. In the case of two parameters, the point describes a surface, called a parametric surface. In all cases, the equations are collectively called a parametric representation, or parametric system, or parameterization (also spelled parametrization, parametrisation) of the object. For example, the equations \begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where is the parameter: A point is on the unit circle if and only if there is a value of such that these two equations generate that point. Sometimes the parametric equations f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Plot
In control theory and stability theory, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer at Siemens in 1930 and the Swedish-American electrical engineer Harry Nyquist at Bell Telephone Laboratories in 1932, is a graphical technique for determining the stability of a linear dynamical system. Because it only looks at the Nyquist plot of the open loop systems, it can be applied without explicitly computing the poles and zeros of either the closed-loop or open-loop system (although the number of each type of right-half-plane singularities must be known). As a result, it can be applied to systems defined by non-rational functions, such as systems with delays. In contrast to Bode plots, it can handle transfer functions with right half-plane singularities. In addition, there is a natural generalization to more complex systems with multiple inputs and multiple outputs, such as control systems fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bode Plots
In electrical engineering and control theory, a Bode plot is a graph of the frequency response of a system. It is usually a combination of a Bode magnitude plot, expressing the magnitude (usually in decibels) of the frequency response, and a Bode phase plot, expressing the phase shift. As originally conceived by Hendrik Wade Bode in the 1930s, the plot is an asymptotic approximation of the frequency response, using straight line segments. Overview Among his several important contributions to circuit theory and control theory, engineer Hendrik Wade Bode, while working at Bell Labs in the 1930s, devised a simple but accurate method for graphing gain and phase-shift plots. These bear his name, ''Bode gain plot'' and ''Bode phase plot''. "Bode" is often pronounced in English as , whereas in Dutch it is usually , closer to English , which is preferred by his family, but less common among researchers.Van Valkenburg, M. E. University of Illinois at Urbana-Champaign, "In m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lyapunov Stability
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Aleksandr Lyapunov. In simple terms, if the solutions that start out near an equilibrium point x_e stay near x_e forever, then x_e is Lyapunov stable. More strongly, if x_e is Lyapunov stable and all solutions that start out near x_e converge to x_e, then x_e is said to be ''asymptotically stable'' (see asymptotic analysis). The notion of '' exponential stability'' guarantees a minimal rate of decay, i.e., an estimate of how quickly the solutions converge. The idea of Lyapunov stability can be extended to infinite-dimensional manifolds, where it is known as structural stability, which concerns the behavior of different but "nearby" solutions to differential equations. Input-to-state stability (ISS ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stability Criterion
In control theory, and especially stability theory, a stability criterion establishes when a system is stable polynomial, stable. A number of stability criteria are in common use: *Circle criterion *Jury stability criterion *Liénard–Chipart criterion *Nyquist stability criterion *Routh–Hurwitz stability criterion *Vakhitov–Kolokolov stability criterion *Barkhausen stability criterion Stability may also be determined by means of root locus analysis. Although the concept of stability is general, there are several narrower definitions through which it may be assessed: * BIBO stability * Linear stability * Lyapunov stability * Orbital stability {{sia Stability theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Operator
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of modules over a ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a linear endomorphism. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Sometimes the term ''linear function'' has the same meaning as ''linear map'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |