|
Nikolay Bogolyubov (paleontologist)
Nikolay Nikolayevich (Mykola Mykolayovych) Bogolyubov (; ; 21 August 1909 – 13 February 1992) was a Soviet, Ukrainian and Russian mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and the theory of dynamical systems; he was the recipient of the 1992 Dirac Medal for his works and studies. Biography Early life (1909–1921) Nikolay Bogolyubov was born on 21 August 1909 in Nizhny Novgorod, Russian Empire to Russian Orthodox Church priest and seminary teacher of theology, psychology and philosophy Nikolay Mikhaylovich Bogolyubov, and Olga Nikolayevna Bogolyubova, a teacher of music. Six months after Nicolay's birth, the family moved to Nizhyn, city of Chernihiv Oblast, where his father taught until 1913. From 1913 to 1918, the family lived in Kyiv. Nikolay received his initial education at home. His father taught him the basics of arithmetic, as well as German, French, and Engl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nizhny Novgorod
Nizhny Novgorod ( ; rus, links=no, Нижний Новгород, a=Ru-Nizhny Novgorod.ogg, p=ˈnʲiʐnʲɪj ˈnovɡərət, t=Lower Newtown; colloquially shortened to Nizhny) is a city and the administrative centre of Nizhny Novgorod Oblast and the Volga Federal District in Russia. The city is located at the confluence of the Oka (river), Oka and the Volga rivers in Central Russia, with a population of over 1.2 million residents, up to roughly 1.7 million residents in the urban agglomeration. Nizhny Novgorod is the List of cities and towns in Russia by population, sixth-largest city in Russia, the Volga#Biggest cities on the shores of the Volga, second-most populous city on the Volga, as well as the Volga Federal District. The city is located 420 kilometers (260 mi) east of Moscow. It is an important economic, transportation, scientific, educational and cultural centre in Russia and the vast Volga-Vyatka economic region, and the main centre of river tourism in Russia. In the his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
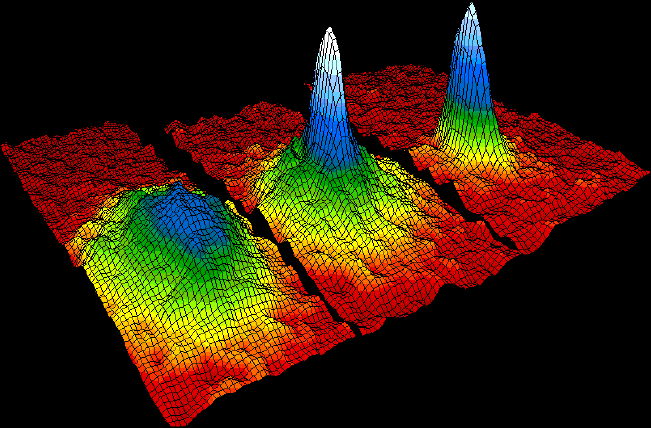
Weakly Interacting Bose Gas
In condensed matter physics, a weakly interacting Bose gas is a quantum mechanical system composed of bosons that interact through low-strength, typically repulsive short-range forces. Unlike the ideal Bose gas, which neglects all interactions, the weakly interacting Bose gas provides a more realistic model for understanding Bose–Einstein condensation and superfluidity. Its behavior is well-described by mean-field theories such as the Gross–Pitaevskii equation and Bogoliubov theory, which capture the effects of interactions on the condensate and its excitations. This model is foundational in the study of ultracold atomic gases, where experimental techniques allow precise control of both the particle density and interaction strength, enabling detailed exploration of quantum statistical phenomena in dilute bosonic systems. The microscopic model was first discussed by Nikolai Bogoliubov in 1947. In one-dimension, the weakly interacting Bose gas is described by the Lieb–Lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace Inequality
In mathematics, there are many kinds of inequalities involving matrices and linear operators on Hilbert spaces. This article covers some important operator inequalities connected with traces of matrices.E. Carlen, Trace Inequalities and Quantum Entropy: An Introductory Course, Contemp. Math. 529 (2010) 73–140 B. Simon, Trace Ideals and their Applications, Cambridge Univ. Press, (1979); Second edition. Amer. Math. Soc., Providence, RI, (2005). Basic definitions Let \mathbf_n denote the space of Hermitian n \times n matrices, \mathbf_n^+ denote the set consisting of positive semi-definite n \times n Hermitian matrices and \mathbf_n^ denote the set of positive definite Hermitian matrices. For operators on an infinite dimensional Hilbert space we require that they be trace class and self-adjoint, in which case similar definitions apply, but we discuss only matrices, for simplicity. For any real-valued function f on an interval I \subseteq \Reals, one may define a matrix function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Krylov–Bogolyubov Theorem
In mathematics, the Krylov–Bogolyubov theorem (also known as the existence of invariant measures theorem) may refer to either of the two related fundamental theorems within the theory of dynamical systems. The theorems guarantee the existence of invariant measures for certain "nice" maps defined on "nice" spaces and were named after Russian- Ukrainian mathematicians and theoretical physicists Nikolay Krylov and Nikolay Bogolyubov who proved the theorems. Zbl. 16.86. Formulation of the theorems Invariant measures for a single map Theorem (Krylov–Bogolyubov). Let ''X'' be a compact, metrizable topological space and ''F'' : ''X'' → ''X'' a continuous map. Then ''F'' admits an invariant Borel probability measure. That is, if Borel(''X'') denotes the Borel σ-algebra generated by the collection ''T'' of open subsets of ''X'', then there exists a probability measure ''μ'' : Borel(''X'') → , 1such that for any subset ''A'' ∈ Borel(''X''), :\mu \left( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
BBGKY Hierarchy
In statistical physics, the Bogoliubov–Born–Green–Kirkwood–Yvon (BBGKY) hierarchy (sometimes called Bogoliubov hierarchy) is a set of equations describing the dynamics of a system of a large number of interacting particles. The equation for an ''s''-particle distribution function (probability density function) in the BBGKY hierarchy includes the (''s'' + 1)-particle distribution function, thus forming a coupled chain of equations. This formal theoretic result is named after Nikolay Bogolyubov, Max Born, Herbert S. Green, John Gamble Kirkwood, and . Formulation The evolution of an ''N''-particle system in absence of quantum fluctuations is given by the Liouville equation for the probability density function f_N = f_N(\mathbf_1 \dots \mathbf_N, \mathbf_1 \dots \mathbf_N, t) in 6''N''-dimensional phase space (3 space and 3 momentum coordinates per particle) \frac + \sum_^N \frac \frac + \sum_^N \mathbf_i \frac = 0, where \mathbf_i, \mathbf_i are the position a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bogoliubov–Parasyuk Theorem
The Bogoliubov–Parasyuk theorem in quantum field theory states that renormalized Green's functions and matrix elements of the scattering matrix (''S''-matrix) are free of ultraviolet divergencies. Green's functions and scattering matrix are the fundamental objects in quantum field theory which determine basic physically measurable quantities. Formal expressions for Green's functions and ''S''-matrix in any physical quantum field theory contain divergent integrals (i.e., integrals which take infinite values) and therefore formally these expressions are meaningless. The renormalization procedure is a specific procedure to make these divergent integrals finite and obtain (and predict) finite values for physically measurable quantities. The Bogoliubov–Parasyuk theorem states that for a wide class of quantum field theories, called renormalizable field theories, these divergent integrals can be made finite in a regular way using a finite (and small) set of certain elementary subtracti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bogoliubov Transformation
In theoretical physics, the Bogoliubov transformation, also known as the Bogoliubov–Valatin transformation, was independently developed in 1958 by Nikolay Bogolyubov and John George Valatin for finding solutions of BCS theory in a homogeneous system. The Bogoliubov transformation is an isomorphism of either the canonical commutation relation algebra or canonical anticommutation relation algebra. This induces an autoequivalence on the respective representations. The Bogoliubov transformation is often used to diagonalize Hamiltonians, which yields the stationary solutions of the corresponding Schrödinger equation. The Bogoliubov transformation is also important for understanding the Unruh effect, Hawking radiation, Davies-Fulling radiation (moving mirror model), pairing effects in nuclear physics, and many other topics. The Bogoliubov transformation is often used to diagonalize Hamiltonians, ''with'' a corresponding transformation of the state function. Operator eigenvalues cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bose–Einstein Condensate
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low Density, densities is cooled to temperatures very close to absolute zero#Relation with Bose–Einstein condensate, absolute zero, i.e. . Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which microscopic Quantum mechanics, quantum-mechanical phenomena, particularly wave interference#Quantum interference, wavefunction interference, become apparent Macroscopic quantum phenomena, macroscopically. More generally, condensation refers to the appearance of macroscopic occupation of one or several states: for example, in BCS theory, a superconductor is a condensate of Cooper pairs. As such, condensation can be associated with phase transition, and the macroscopic occupation of the state is the order parameter. Bose–Einstein condensate was first predicted, generally, in 1924–1925 by Albert Einstein, credit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bogoliubov Quasiparticle
In condensed matter physics, a Bogoliubov quasiparticle or Bogoliubon is a quasiparticle that occurs in superconductors. Whereas superconductivity is characterized by the condensation of Cooper pairs into the same ground quantum state, Bogoliubov quasiparticles are elementary excitations above the ground state, which are superpositions (linear combinations) of the excitations of negatively charged electrons and positively charged electron holes, and are therefore neutral spin-½ fermions. These quasiparticles are named after Nikolay Bogolyubov. Sometimes these quasiparticles are also called Majorana modes, in analogy with the equations for Majorana fermions. When dealing with conventional superconductors, interference between Bogoliubov quasiparticles is hard for a Scanning Tunneling Microscope A scanning tunneling microscope (STM) is a type of scanning probe microscope used for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Freiman%27s Theorem
In additive combinatorics, a discipline within mathematics, Freiman's theorem is a central result which indicates the approximate structure of sets whose sumset is small. It roughly states that if , A+A, /, A, is small, then A can be contained in a small generalized arithmetic progression. Statement If A is a finite subset of \mathbb with , A+A, \le K, A, , then A is contained in a generalized arithmetic progression of dimension at most d(K) and size at most f(K), A, , where d(K) and f(K) are constants depending only on K. Examples For a finite set A of integers, it is always true that :, A + A, \ge 2, A, -1, with equality precisely when A is an arithmetic progression. More generally, suppose A is a subset of a finite proper generalized arithmetic progression P of dimension d such that , P, \le C, A, for some real C \ge 1. Then , P+P, \le 2^d , P, , so that :, A+A, \le , P+P, \le 2^d , P, \le C2^d, A, . History of Freiman's theorem This result is due to Gregory Freim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bogoliubov Inner Product
The Bogoliubov inner product (also known as the Duhamel two-point function, Bogolyubov inner product, Bogoliubov scalar product, or Kubo–Mori–Bogoliubov inner product) is a special inner product in the space of operators. The Bogoliubov inner product appears in quantum statistical mechanicsD. P. SankovichOn the Bose condensation in some model of a nonideal Bose gas '' J. Math. Phys.'' 45, 4288 (2004). and is named after theoretical physicist Nikolay Bogoliubov. Definition Let A be a self-adjoint operator. The Bogoliubov inner product of any two operators X and Y is defined as : \langle X,Y\rangle_A=\int\limits_0^1 ^ X^\dagger^Yx The Bogoliubov inner product satisfies all the axioms of the inner product: it is sesquilinear, positive semidefinite (i.e., \langle X,X\rangle_A\ge 0), and satisfies the symmetry property \langle X,Y\rangle_A=(\langle Y,X\rangle_A)^* where \alpha^* is the complex conjugate of \alpha. In applications to quantum statistical mechanics, the operator A h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |