|
Newsvendor Model
The newsvendor (or newsboy or single-periodWilliam J. Stevenson, Operations Management. 10th edition, 2009; page 581 or salvageable) model is a mathematical model in operations management and applied economics used to determine optimal inventory levels. It is (typically) characterized by fixed prices and uncertain demand for a perishable product. If the inventory level is q, each unit of demand above q is lost in potential sales. This model is also known as the ''newsvendor problem'' or ''newsboy problem'' by analogy with the situation faced by a newspaper vendor who must decide how many copies of the day's paper to stock in the face of uncertain demand and knowing that unsold copies will be worthless at the end of the day. History The mathematical problem appears to date from 1888 where Edgeworth used the central limit theorem to determine the optimal cash reserves to satisfy random withdrawals from depositors. According to Chen, Cheng, Choi and Wang (2016), the term "news ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution supported on the real numbers, discrete or "mixed" as well as continuous, is uniquely identified by an ''upwards continuous'' ''monotonic increasing'' cumulative distribution function F : \mathbb R \rightarrow ,1/math> satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from minus infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability that the random variable X takes on a value less ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inventory Control System
Inventory control or stock control can be broadly defined as "the activity of checking a shop's stock". It is the process of ensuring that the right amount of supply is available within a business. However, a more focused definition takes into account the more science-based, methodical practice of not only verifying a business's inventory but also maximising the amount of profit from the least amount of inventory investment without affecting customer satisfaction. Other facets of inventory control include forecasting future demand, supply chain management, production control, financial flexibility, purchasing data, loss prevention and turnover, and customer satisfaction. An extension of inventory control is the inventory control system. This may come in the form of a technological system and its programmed software used for managing various aspects of inventory problems, or it may refer to a methodology (which may include the use of technological barriers) for handling loss preve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reorder Point
The reorder point (ROP) is the level of inventory which triggers an action to replenish that particular inventory stock. It is a minimum amount of an item which a firm holds in stock, such that, when stock falls to this amount, the item must be reordered. It is normally calculated as the forecast usage during the replenishment lead time plus safety stock. In the EOQ (Economic Order Quantity) model, it was assumed that there is no time lag between ordering and procuring of materials. Continuous Review System The reorder point for replenishment of stock occurs when the level of inventory drops down to zero. In view of instantaneous replenishment of stock the level of inventory jumps to the original level from zero level. In real life situations one never encounters a zero lead time. There is always a time lag from the date of placing an order for material and the date on which materials are received. As a result the reorder point is always higher than zero, and if the firm places t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economic Lot Scheduling Problem
The economic lot scheduling problem (ELSP) is a problem in operations management and inventory theory that has been studied by many researchers for more than 50 years. The term was first used in 1958 by professor Jack D. Rogers of Berkeley, who extended the economic order quantity model to the case where there are several products to be produced on the same machine, so that one must decide both the lot size for each product and when each lot should be produced. The method illustrated by Jack D. Rogers draws on a 1956 paper from Welch, W. Evert. The ELSP is a mathematical model of a common issue for almost any company or industry: planning what to manufacture, when to manufacture and how much to manufacture. Model formulation The classic ELSP is concerned with scheduling the production of several products on a single machine in order to minimize the total costs incurred (which include setup costs and inventory holding costs). We assume a known, non-varying demand d_j, j=1,\cdots, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Lot Size Model
The dynamic lot-size model in inventory theory, is a generalization of the economic order quantity model that takes into account that demand for the product varies over time. The model was introduced by Harvey M. Wagner and Thomson M. Whitin in 1958.Harvey M. Wagner and Thomson M. Whitin, "Dynamic version of the economic lot size model," Management Science, Vol. 5, pp. 89–96, 1958 Problem setup We have available a forecast of product demand over a relevant time horizon t=1,2,...,N (for example we might know how many widgets will be needed each week for the next 52 weeks). There is a setup cost incurred for each order and there is an inventory holding cost per item per period ( and can also vary with time if desired). The problem is how many units to order now to minimize the sum of setup cost and inventory cost. Let us denote inventory: I=I_+\sum_^x_-\sum_^d_\geq0 The functional equation representing minimal cost policy is: f_(I)=\underset\left i_I+H(x_)s_+f_\lef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economic Production Quantity
The economic production quantity model (also known as the EPQ model) determines the quantity a company or retailer should order to minimize the total inventory costs by balancing the inventory holding cost and average fixed ordering cost. The EPQ model was developed by E.W. Taft in 1918. This method is an extension of the economic order quantity model (also known as the EOQ model). The difference between these two methods is that the EPQ model assumes the company will produce its own quantity or the parts are going to be shipped to the company while they are being produced, therefore the orders are available or received in an incremental manner while the products are being produced. While the EOQ model assumes the order quantity arrives complete and immediately after ordering, meaning that the parts are produced by another company and are ready to be shipped when the order is placed. In some literature, "economic manufacturing quantity" model (EMQ) is used for "economic productio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
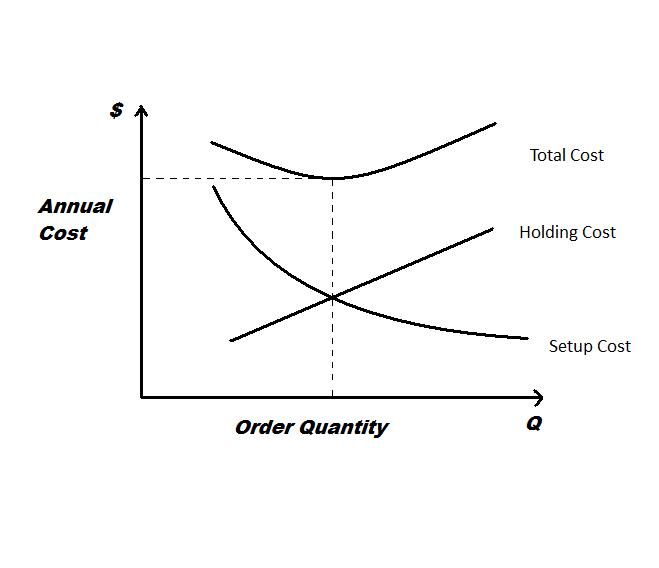
Economic Order Quantity
Economic Order Quantity (EOQ), also known as Economic Buying Quantity (EPQ), is the order quantity that minimizes the total holding costs and ordering costs in inventory management. It is one of the oldest classical production scheduling models. The model was developed by Ford W. Harris in 1913, but R. H. Wilson, a consultant who applied it extensively, and K. Andler are given credit for their in-depth analysis. Overview EOQ applies only when demand for a product is constant over the year and each new order is delivered in full when inventory reaches zero. There is a fixed cost for each order placed, regardless of the number of units ordered; an order is assumed to contain only 1 unit. There is also a cost for each unit held in storage, commonly known as holding cost, sometimes expressed as a percentage of the purchase cost of the item. While the EOQ formulation is straightforward there are factors such as transportation rates and quantity discounts to consider in actual appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lognormal Distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable is log-normally distributed, then has a normal distribution. Equivalently, if has a normal distribution, then the exponential function of , , has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. It is a convenient and useful model for measurements in exact and engineering sciences, as well as medicine, economics and other topics (e.g., energies, concentrations, lengths, prices of financial instruments, and other metrics). The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton. The log-normal distribution has also been associated with other names, such as McAlister, Gibrat and Cobb–Douglas. A log-normal process is the statistical realization of the multipl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. Standard deviation may be abbreviated SD, and is most commonly represented in mathematical texts and equations by the lower case Greek letter σ (sigma), for the population standard deviation, or the Latin letter '' s'', for the sample standard deviation. The standard deviation of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance. It is algebraically simpler, though in practice less robust, than the average absolute deviation. A useful property of the standard deviation is that, unlike the variance, it is expressed in the same unit as the data. The standard deviation o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of symmetric probability distributions. The distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds. The bounds are defined by the parameters, ''a'' and ''b'', which are the minimum and maximum values. The interval can either be closed (e.g. , b or open (e.g. (a, b)). Therefore, the distribution is often abbreviated ''U'' (''a'', ''b''), where U stands for uniform distribution. The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable ''X'' under no constraint other than that it is contained in the distribution's support. Definitions Probability density function The probability density function of the continuous uniform distribution is: : f(x)=\be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |