|
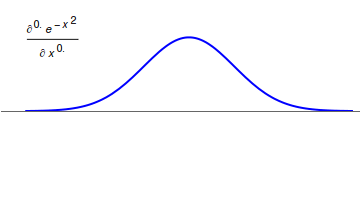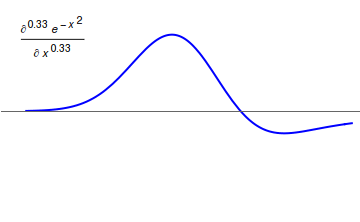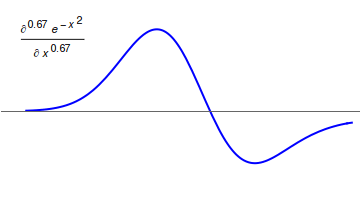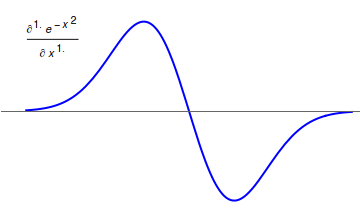
Neopolarogram
The term neopolarogram refers to mathematical derivatives of polarography, polarograms or cyclic voltammetry, cyclic voltammograms that in effect deconvolute diffusion and electrochemical kinetics. This is achieved by analog or digital implementations of fractional calculus.Keith Oldham, Jerome Spanier; ''The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order'' (Dover Books on Mathematics) The implementation of fractional derivative calculations by means of numerical methods is straight forward. The G1- (Grünwald–Letnikov derivative) and the RL0-algorithms (Riemann–Liouville integral) are recursive methods to implement a numerical calculation of fractional differintegrals. Yet differintegrals are faster to compute in discrete fourier space using fast Fourier transform, FFT.Jun-Sheng Yu, Zu-Xun Zhanga; "Differentiation, semidifferentiation and semi-integration of a digital signals based on Fourier transformations"; ''Journal of Elec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abscissa
In common usage, the abscissa refers to the (''x'') coordinate and the ordinate refers to the (''y'') coordinate of a standard two-dimensional graph. The distance of a point from the y-axis, scaled with the x-axis, is called abscissa or x coordinate of the point. The distance of a point from x-axis scaled with the y-axis is called ordinate. For example, if (x, y) is an ordered pair in the Cartesian plane, then the first coordinate in the plane (x) is called the abscissa and the second coordinate (y) is the ordinate. In mathematics, the abscissa (; plural ''abscissae'' or ''abscissas'') and the ordinate are respectively the first and second coordinate of a point in a Cartesian coordinate system: :abscissa \equiv x-axis (horizontal) coordinate :ordinate \equiv y-axis (vertical) coordinate Usually these are the horizontal and vertical coordinates of a point in plane, the rectangular coordinate system. An ordered pair consists of two terms—the abscissa (horizontal, usuall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahydrofuran
Tetrahydrofuran (THF), or oxolane, is an organic compound with the formula (CH2)4O. The compound is classified as heterocyclic compound, specifically a cyclic ether. It is a colorless, water- miscible organic liquid with low viscosity. It is mainly used as a precursor to polymers. Being polar and having a wide liquid range, THF is a versatile solvent. Production About 200,000 tonnes of tetrahydrofuran are produced annually. The most widely used industrial process involves the acid-catalyzed dehydration of 1,4-butanediol. Ashland/ISP is one of the biggest producers of this chemical route. The method is similar to the production of diethyl ether from ethanol. The butanediol is derived from condensation of acetylene with formaldehyde followed by hydrogenation. DuPont developed a process for producing THF by oxidizing ''n''-butane to crude maleic anhydride, followed by catalytic hydrogenation. A third major industrial route entails hydroformylation of allyl alcohol foll ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
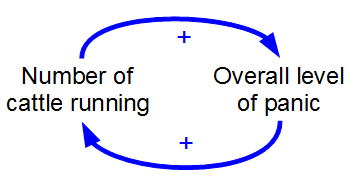
Positive Feedback
Positive feedback (exacerbating feedback, self-reinforcing feedback) is a process that occurs in a feedback loop which exacerbates the effects of a small disturbance. That is, the effects of a perturbation on a system include an increase in the magnitude of the perturbation. That is, ''A produces more of B which in turn produces more of A''.Keesing, R.M. (1981). Cultural anthropology: A contemporary perspective (2nd ed.) p.149. Sydney: Holt, Rinehard & Winston, Inc. In contrast, a system in which the results of a change act to reduce or counteract it has negative feedback. Both concepts play an important role in science and engineering, including biology, chemistry, and cybernetics. Mathematically, positive feedback is defined as a positive loop gain around a closed loop of cause and effect. That is, positive feedback is in phase with the input, in the sense that it adds to make the input larger. Positive feedback tends to cause system instability. When the loop gain is p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sigmoid Function
A sigmoid function is a mathematical function having a characteristic "S"-shaped curve or sigmoid curve. A common example of a sigmoid function is the logistic function shown in the first figure and defined by the formula: :S(x) = \frac = \frac=1-S(-x). Other standard sigmoid functions are given in the Examples section. In some fields, most notably in the context of artificial neural networks, the term "sigmoid function" is used as an alias for the logistic function. Special cases of the sigmoid function include the Gompertz curve (used in modeling systems that saturate at large values of x) and the ogee curve (used in the spillway of some dams). Sigmoid functions have domain of all real numbers, with return (response) value commonly monotonically increasing but could be decreasing. Sigmoid functions most often show a return value (y axis) in the range 0 to 1. Another commonly used range is from −1 to 1. A wide variety of sigmoid functions including the logistic and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ohm's Law
Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equation that describes this relationship: :I = \frac, where is the current through the conductor, ''V'' is the voltage measured ''across'' the conductor and ''R'' is the resistance of the conductor. More specifically, Ohm's law states that the ''R'' in this relation is constant, independent of the current. If the resistance is not constant, the previous equation cannot be called ''Ohm's law'', but it can still be used as a definition of static/DC resistance. Ohm's law is an empirical relation which accurately describes the conductivity of the vast majority of electrically conductive materials over many orders of magnitude of current. However some materials do not obey Ohm's law; these are called non-ohmic. The law was named after the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Family Of Curves
In geometry, a family of curves is a set of curves, each of which is given by a function or parametrization in which one or more of the parameters is variable. In general, the parameter(s) influence the shape of the curve in a way that is more complicated than a simple linear transformation. Sets of curves given by an implicit relation may also represent families of curves. Families of curves appear frequently in solutions of differential equations; when an additive constant of integration is introduced, it will usually be manipulated algebraically until it no longer represents a simple linear transformation. Families of curves may also arise in other areas. For example, all non-degenerate conic sections can be represented using a single polar equation with one parameter, the eccentricity of the curve: :r(\theta) = as the value of changes, the appearance of the curve varies in a relatively complicated way. Applications Families of curves may arise in various topi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Randles–Sevcik Equation
In cyclic voltammetry, the Randles–Ševčík equation describes the effect of scan rate on the peak current ''ip''. For simple redox events such as the ferrocene/ferrocenium couple, ''ip'' depends not only on the concentration and diffusional properties of the electroactive species but also on scan rate. :i_p = 0.4463 \ nFAC \left(\frac\right)^ Or if the solution is at 25 °C: Allen J. Bard and Larry R. Faulkner, "Electrochemical Methods: Fundamentals and Applications" (2nd ed.) John Wiley & Sons 2001. :i_p = 2.69\times 10^ \ n^ AD^ Cv^ *''ip'' = current maximum in amps *''n'' = number of electrons transferred in the redox event (usually 1) *''A'' = electrode area in cm2 *''F'' = Faraday constant, Faraday Constant in C mol−1 *''D'' = diffusion coefficient in cm2/s *''C'' = concentration in mol/cm3 *''ν'' = scan rate in V/s *''R'' = Gas constant in J K−1 mol−1 *''T'' = temperature in K * The constant with a value of 2.69x105 has units of C mol−1 V−1/2 For n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
FWHM
In a distribution, full width at half maximum (FWHM) is the difference between the two values of the independent variable at which the dependent variable is equal to half of its maximum value. In other words, it is the width of a spectrum curve measured between those points on the ''y''-axis which are half the maximum amplitude. Half width at half maximum (HWHM) is half of the FWHM if the function is symmetric. The term full duration at half maximum (FDHM) is preferred when the independent variable is time. FWHM is applied to such phenomena as the duration of pulse waveforms and the spectral width of sources used for optical communications and the resolution of spectrometers. The convention of "width" meaning "half maximum" is also widely used in signal processing to define bandwidth as "width of frequency range where less than half the signal's power is attenuated", i.e., the power is at least half the maximum. In signal processing terms, this is at most −3 dB of attenua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |