 |
Multidimensional Spectral Estimation
Multidimension spectral estimation is a generalization of spectral estimation, normally formulated for one-dimensional signals, to multidimensional signals or multivariate data, such as wave vectors. Motivation Multidimensional spectral estimation has gained popularity because of its application in fields like medicine, aerospace, sonar, radar, bio informatics and geophysics. In the recent past, a number of methods have been suggested to design models with finite parameters to estimate the power spectrum of multidimensional signals. In this article, we will be looking into the basics of methods used to estimate the power spectrum of multidimensional signals. Applications There are many applications of spectral estimation of multi-D signals such as classification of signals as low pass, high pass, pass band and stop band. It is also used in compression and coding of audio and video signals, beam forming and direction finding in radars, Seismic data estimation and processing, array ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
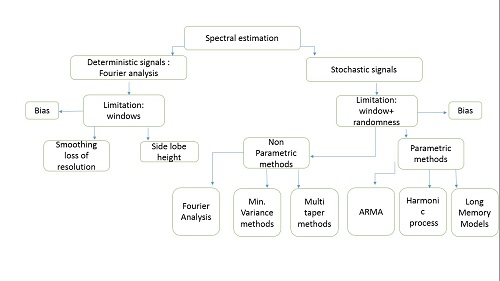
Spectral Estimation
In statistical signal processing, the goal of spectral density estimation (SDE) or simply spectral estimation is to estimate the spectral density (also known as the power spectral density) of a signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities. Some SDE techniques assume that a signal is composed of a limited (usually small) number of generating frequencies plus noise and seek to find the location and intensity of the generated frequencies. Others make no assumption on the number of components and seek to estimate the whole generating spectrum. Overview Spectrum analysis, also referred to as frequency domain analysis or spectral density estimation, is the technical process of decomposing a complex signal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication. The thermodynamic concept was referred to by Scottish scientist and engineer William Rankine in 1850 with the names ''thermodynamic function'' and ''heat-potential''. In 1865, German physicist Rudolf Clausius, one of the leading founders of the field of thermodynamics, defined it as the quotient of an infinitesimal amount ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Principle Of Maximum Entropy
The principle of maximum entropy states that the probability distribution which best represents the current state of knowledge about a system is the one with largest entropy, in the context of precisely stated prior data (such as a proposition that expresses testable information). Another way of stating this: Take precisely stated prior data or testable information about a probability distribution function. Consider the set of all trial probability distributions that would encode the prior data. According to this principle, the distribution with maximal information entropy is the best choice. History The principle was first expounded by E. T. Jaynes in two papers in 1957 where he emphasized a natural correspondence between statistical mechanics and information theory. In particular, Jaynes offered a new and very general rationale why the Gibbsian method of statistical mechanics works. He argued that the entropy of statistical mechanics and the information entropy of informa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Maximum Likelihood
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference. If the likelihood function is differentiable, the derivative test for finding maxima can be applied. In some cases, the first-order conditions of the likelihood function can be solved analytically; for instance, the ordinary least squares estimator for a linear regression model maximizes the likelihood when all observed outcomes are assumed to have Normal distributions with the same variance. From the perspective of Bayesian in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Max Entropy Spectral Estimation
Max or MAX may refer to: Animals * Max (dog) (1983–2013), at one time purported to be the world's oldest living dog * Max (English Springer Spaniel), the first pet dog to win the PDSA Order of Merit (animal equivalent of OBE) * Max (gorilla) (1971–2004), a western lowland gorilla at the Johannesburg Zoo who was shot by a criminal in 1997 Brands and enterprises * Australian Max Beer * Max Hamburgers, a fast-food corporation * MAX Index, a Hungarian domestic government bond index * Max Fashion, an Indian clothing brand Computing * MAX (operating system), a Spanish-language Linux version * Max (software), a music programming language * Commodore MAX Machine * Multimedia Acceleration eXtensions, extensions for HP PA-RISC Films * ''Max'' (1994 film), a Canadian film by Charles Wilkinson * ''Max'' (2002 film), a film about Adolf Hitler * ''Max'' (2015 film), an American war drama film Games * ''Dancing Stage Max'', a 2005 game in the ''Dance Dance Revolution'' series * ''DDRMA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Linear Prediction
Linear prediction is a mathematical operation where future values of a discrete-time signal are estimated as a linear function of previous samples. In digital signal processing, linear prediction is often called linear predictive coding (LPC) and can thus be viewed as a subset of filter theory. In system analysis, a subfield of mathematics, linear prediction can be viewed as a part of mathematical modelling or optimization. The prediction model The most common representation is :\widehat(n) = \sum_^p a_i x(n-i)\, where \widehat(n) is the predicted signal value, x(n-i) the previous observed values, with p \leq n , and a_i the predictor coefficients. The error generated by this estimate is :e(n) = x(n) - \widehat(n)\, where x(n) is the true signal value. These equations are valid for all types of (one-dimensional) linear prediction. The differences are found in the way the predictor coefficients a_i are chosen. For multi-dimensional signals the error metric is often defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Autoregressive
In statistics, econometrics and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it is used to describe certain time-varying processes in nature, economics, etc. The autoregressive model specifies that the output variable depends linearly on its own previous values and on a stochastic term (an imperfectly predictable term); thus the model is in the form of a stochastic difference equation (or recurrence relation which should not be confused with differential equation). Together with the moving-average (MA) model, it is a special case and key component of the more general autoregressive–moving-average (ARMA) and autoregressive integrated moving average (ARIMA) models of time series, which have a more complicated stochastic structure; it is also a special case of the vector autoregressive model (VAR), which consists of a system of more than one interlocking stochastic difference equation in more than one evolving random vari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Classical Estimate
Classical may refer to: European antiquity *Classical antiquity, a period of history from roughly the 7th or 8th century B.C.E. to the 5th century C.E. centered on the Mediterranean Sea *Classical architecture, architecture derived from Greek and Roman architecture of classical antiquity *Classical mythology, the body of myths from the ancient Greeks and Romans *Classical tradition, the reception of classical Greco-Roman antiquity by later cultures * Classics, study of the language and culture of classical antiquity, particularly its literature *Classicism, a high regard for classical antiquity in the arts Music and arts *Classical ballet, the most formal of the ballet styles * Classical music, a variety of Western musical styles from the 9th century to the present * Classical guitar, a common type of acoustic guitar *Classical Hollywood cinema, a visual and sound style in the American film industry between 1927 and 1963 * Classical Indian dance, various codified art forms whose t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Spectral Estimation Techniques
''Spectral'' is a 2016 3D military science fiction, supernatural horror fantasy and action-adventure thriller war film directed by Nic Mathieu. Written by himself, Ian Fried, and George Nolfi from a story by Fried and Mathieu. The film stars James Badge Dale, Max Martini, Emily Mortimer, Clayne Crawford and Bruce Greenwood. The film was released worldwide on December 9, 2016 on Netflix. On February 1, 2017, Netflix released a prequel graphic novel of the film called ''Spectral: Ghosts of War'' which was made available digitally through the website ComiXology. Plot DARPA researcher Dr. Mark Clyne flies from Virginia to Moldova, the current deployment location of the US military in the ongoing Moldovan War, to be consulted on one of his creations, a line of hyperspectral imaging goggles that have been issued to troops there. After arriving at a US military airbase on the outskirts of Chișinău, he meets with US Army General Orland and CIA officer Fran Madison. They show him fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Mean Square Error
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate. In machine learning, specifically empirical risk minimization, MSE may refer to the ''empirical'' risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution). The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the er ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Signal
In signal processing, a signal is a function that conveys information about a phenomenon. Any quantity that can vary over space or time can be used as a signal to share messages between observers. The '' IEEE Transactions on Signal Processing'' includes audio, video, speech, image, sonar, and radar as examples of signal. A signal may also be defined as observable change in a quantity over space or time (a time series), even if it does not carry information. In nature, signals can be actions done by an organism to alert other organisms, ranging from the release of plant chemicals to warn nearby plants of a predator, to sounds or motions made by animals to alert other animals of food. Signaling occurs in all organisms even at cellular levels, with cell signaling. Signaling theory, in evolutionary biology, proposes that a substantial driver for evolution is the ability of animals to communicate with each other by developing ways of signaling. In human engineering, signals are t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |