|
Mooney–Rivlin Solid
In continuum mechanics, a Mooney–Rivlin solidMooney, M., 1940, ''A theory of large elastic deformation'', Journal of Applied Physics, 11(9), pp. 582–592.Rivlin, R. S., 1948, ''Large elastic deformations of isotropic materials. IV. Further developments of the general theory'', Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 241(835), pp. 379–397. is a hyperelastic material model where the strain energy density function W\, is a linear combination of two invariants of the left Cauchy–Green deformation tensor \boldsymbol. The model was proposed by Melvin Mooney in 1940 and expressed in terms of invariants by Ronald Rivlin in 1948. The strain energy density function for an incompressible Mooney–Rivlin material is :W = C_ (\bar_1-3) + C_ (\bar_2-3), \, where C_ and C_ are empirically determined material constants, and \bar I_1 and \bar I_2 are the first and the second invariant of \bar \boldsymbol B = (\det \bol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Mechanics
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents. Solid mechanics is fundamental for civil, aerospace, nuclear, biomedical and mechanical engineering, for geology, and for many branches of physics such as materials science. It has specific applications in many other areas, such as understanding the anatomy of living beings, and the design of dental prostheses and surgical implants. One of the most common practical applications of solid mechanics is the Euler–Bernoulli beam equation. Solid mechanics extensively uses tensors to describe stresses, strains, and the relationship between them. Solid mechanics is a vast subject because of the wide range of solid materials available, such as steel, wood, concrete, biological materials, textiles, geologica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bulk Modulus
The bulk modulus (K or B) of a substance is a measure of how resistant to compression the substance is. It is defined as the ratio of the infinitesimal pressure increase to the resulting ''relative'' decrease of the volume. Other moduli describe the material's response ( strain) to other kinds of stress: the shear modulus describes the response to shear stress, and Young's modulus describes the response to normal (lengthwise stretching) stress. For a fluid, only the bulk modulus is meaningful. For a complex anisotropic solid such as wood or paper, these three moduli do not contain enough information to describe its behaviour, and one must use the full generalized Hooke's law. The reciprocal of the bulk modulus at fixed temperature is called the isothermal compressibility. Definition The bulk modulus K (which is usually positive) can be formally defined by the equation :K=-V\frac , where P is pressure, V is the initial volume of the substance, and dP/dV denotes the derivative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-Newtonian Fluids
A non-Newtonian fluid is a fluid that does not follow Newton's law of viscosity, i.e., constant viscosity independent of stress. In non-Newtonian fluids, viscosity can change when under force to either more liquid or more solid. Ketchup, for example, becomes runnier when shaken and is thus a non-Newtonian fluid. Many salt solutions and molten polymers are non-Newtonian fluids, as are many commonly found substances such as custard, toothpaste, starch suspensions, corn starch, paint, blood, melted butter, and shampoo. Most commonly, the viscosity (the gradual deformation by shear or tensile stresses) of non-Newtonian fluids is dependent on shear rate or shear rate history. Some non-Newtonian fluids with shear-independent viscosity, however, still exhibit normal stress-differences or other non-Newtonian behavior. In a Newtonian fluid, the relation between the shear stress and the shear rate is linear, passing through the origin, the constant of proportionality being the coefficien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strain Energy Density Function
A strain energy density function or stored energy density function is a scalar-valued function that relates the strain energy density of a material to the deformation gradient. : W = \hat(\boldsymbol) = \hat(\boldsymbol^T\cdot\boldsymbol) =\bar(\boldsymbol) = \bar(\boldsymbol^\cdot\boldsymbol)=\tilde(\boldsymbol,\boldsymbol) Equivalently, : W = \hat(\boldsymbol) = \hat(\boldsymbol^T\cdot\boldsymbol\cdot\boldsymbol) =\tilde(\boldsymbol,\boldsymbol) where \boldsymbol is the (two-point) deformation gradient tensor, \boldsymbol is the right Cauchy–Green deformation tensor, \boldsymbol is the left Cauchy–Green deformation tensor, and \boldsymbol is the rotation tensor from the polar decomposition of \boldsymbol. For an anisotropic material, the strain energy density function \hat(\boldsymbol) depends implicitly on reference vectors or tensors (such as the initial orientation of fibers in a composite) that characterize internal material texture. The spatial represe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century. Explanation A continuum model assumes that the substance of the object fills the space it occupies. Modeling objects in this way ignores the fact that matter is made of atoms, and so is not continuous; however, on length scales much greater than that of inter-atomic distances, such models are highly accurate. These models can be used to derive differential equations that describe the behavior of such objects using physical laws, such as mass conservation, momentum conservation, and energy conservation, and some information about the material is provided by constitutive relationships. Continuum mechanics deals with the physical properties of solids and fluids which are independent of any particular coordinate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Strain Theory
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue. Displacement The displacement of a body has two components: a rigid-body displacement and a deformation. * A rigid-body displacement consists of a simultaneous translation (physics) and rotation of the body without changing its shape or size. * Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration \kappa_0(\mathcal B) to a current or deformed configuration \kappa_t(\mathcal B) (Figure 1). A change in the conf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperelastic Material
A hyperelastic or Green elastic materialR.W. Ogden, 1984, ''Non-Linear Elastic Deformations'', , Dover. is a type of constitutive model for ideally elastic material for which the stress–strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material. For many materials, linear elastic models do not accurately describe the observed material behaviour. The most common example of this kind of material is rubber, whose stress- strain relationship can be defined as non-linearly elastic, isotropic and incompressible. Hyperelasticity provides a means of modeling the stress–strain behavior of such materials. The behavior of unfilled, vulcanized elastomers often conforms closely to the hyperelastic ideal. Filled elastomers and biological tissues are also often modeled via the hyperelastic idealization. Ronald Rivlin and Melvin Mooney developed the first hyperelastic models, the Neo-Hookean and Mooney ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neo-Hookean Solid
A neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, the stress-strain curve of a neo-Hookean material is not linear. Instead, the relationship between applied stress and strain is initially linear, but at a certain point the stress-strain curve will plateau. The neo-Hookean model does not account for the dissipative release of energy as heat while straining the material and perfect elasticity is assumed at all stages of deformation. The neo-Hookean model is based on the statistical thermodynamics of cross-linked polymer chains and is usable for plastics and rubber-like substances. Cross-linked polymers will act in a neo-Hookean manner because initially the polymer chains can move relative to each other when a stress is applied. However, at a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
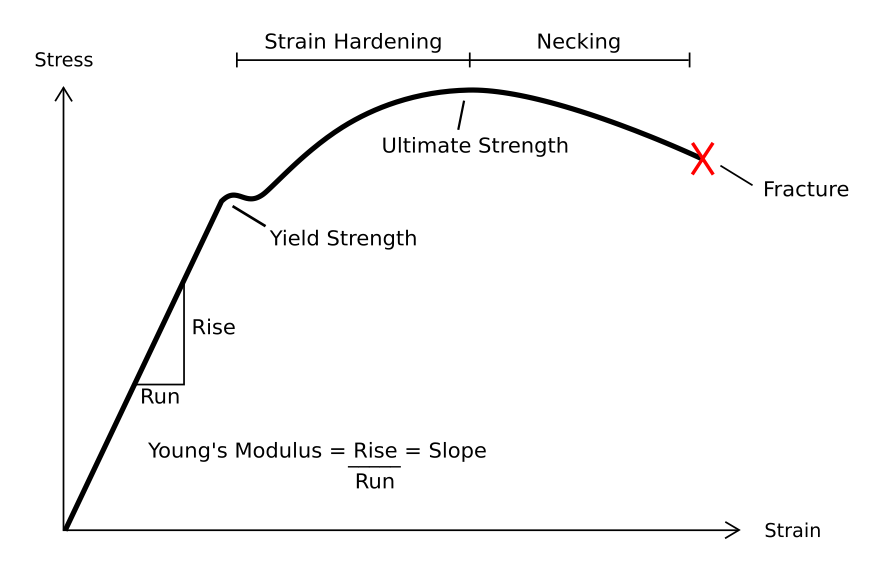
Engineering Stress
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a structur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cayley–Hamilton Theorem
In linear algebra, the Cayley–Hamilton theorem (named after the mathematicians Arthur Cayley and William Rowan Hamilton) states that every square matrix over a commutative ring (such as the real or complex numbers or the integers) satisfies its own characteristic equation. If is a given matrix and is the identity matrix, then the characteristic polynomial of is defined as p_A(\lambda)=\det(\lambda I_n-A), where is the determinant operation and is a variable for a scalar element of the base ring. Since the entries of the matrix (\lambda I_n-A) are (linear or constant) polynomials in , the determinant is also a degree- monic polynomial in , p_A(\lambda) = \lambda^n + c_\lambda^ + \cdots + c_1\lambda + c_0~. One can create an analogous polynomial p_A(A) in the matrix instead of the scalar variable , defined as p_A(A) = A^n + c_A^ + \cdots + c_1A + c_0I_n~. The Cayley–Hamilton theorem states that this polynomial expression is equal to the zero matrix, which is to sa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and even by industry. Further, both spellings are often used ''within'' a particular industry or country. Industries in British English-speaking countries typically use the "gauge" spelling. is the pressure relative to the ambient pressure. Various units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the SI unit of pressure, the pascal (Pa), for example, is one newton per square metre (N/m2); similarly, the pound-force per square inch ( psi) is the traditional unit of pressure in the imperial and U.S. customary systems. Pressure may also be expressed in terms of standard atmospheric pressure; the atmosphere (atm) is equal to this pressure, and the torr is defined as of this. Manome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)