engineering stress on:
[Wikipedia]
[Google]
[Amazon]
In
 In the above definitions of engineering stress and strain, two behaviors of materials in tensile tests are ignored:
* the shrinking of section area
* compounding development of elongation
''True stress'' and ''true strain'' are defined differently than engineering stress and strain to account for these behaviors. They are given as
:
Here the dimensions are instantaneous values. Assuming volume of the sample conserves and deformation happens uniformly,
:
The true stress and strain can be expressed by engineering stress and strain. For true stress,
:
For the strain,
:
Integrate both sides and apply the boundary condition,
:
So in a tension test, true stress is larger than engineering stress and true strain is less than engineering strain. Thus, a point defining true stress–strain curve is displaced upwards and to the left to define the equivalent engineering stress–strain curve. The difference between the true and engineering stresses and strains will increase with
In the above definitions of engineering stress and strain, two behaviors of materials in tensile tests are ignored:
* the shrinking of section area
* compounding development of elongation
''True stress'' and ''true strain'' are defined differently than engineering stress and strain to account for these behaviors. They are given as
:
Here the dimensions are instantaneous values. Assuming volume of the sample conserves and deformation happens uniformly,
:
The true stress and strain can be expressed by engineering stress and strain. For true stress,
:
For the strain,
:
Integrate both sides and apply the boundary condition,
:
So in a tension test, true stress is larger than engineering stress and true strain is less than engineering strain. Thus, a point defining true stress–strain curve is displaced upwards and to the left to define the equivalent engineering stress–strain curve. The difference between the true and engineering stresses and strains will increase with
 Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
 On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
, deformation (the change in size or shape of an object) may be ''elastic'' or ''plastic''.
If the deformation is negligible, the object is said to be ''rigid''.
Main concepts
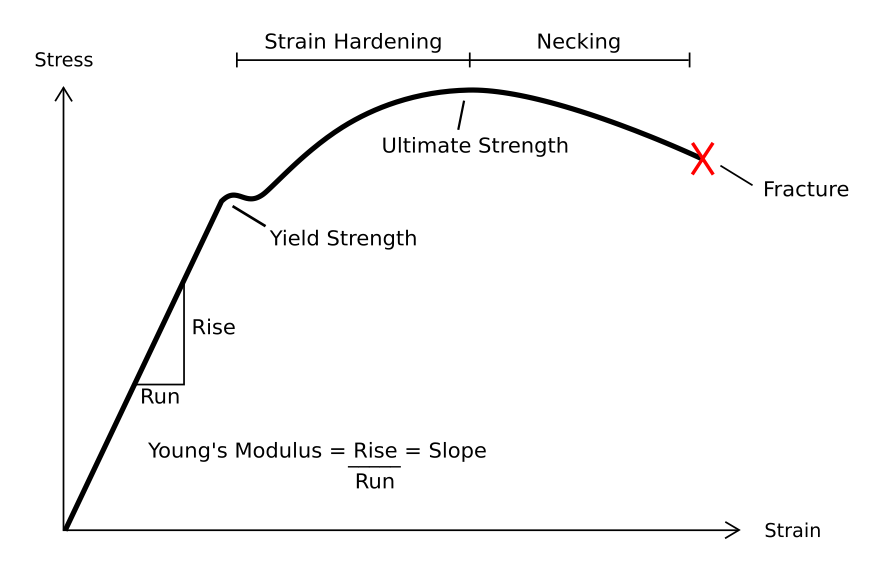
Occurrence of deformation in engineering applications is based on the following background concepts: * ''Displacements'' are any change in position of a point on the object, including whole-body translations and rotations ( rigid transformations). * ''Deformation'' are changes in the relative position between internals points on the object, excluding rigid transformations, causing the body to change shape or size. * ''Strain'' is the ''relative'' ''internal'' deformation, the dimensionless change in shape of an infinitesimal cube of material relative to a reference configuration. Mechanical strains are caused by mechanical stress, ''see stress-strain curve''. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation iselastic
Elastic is a word often used to describe or identify certain types of elastomer, Elastic (notion), elastic used in garments or stretch fabric, stretchable fabrics.
Elastic may also refer to:
Alternative name
* Rubber band, ring-shaped band of rub ...
. Elasticity in materials occurs when applied stress does not surpass the energy required to break molecular bonds, allowing the material to deform reversibly and return to its original shape once the stress is removed. The linear relationship for a material is known as Young's modulus
Young's modulus (or the Young modulus) is a mechanical property of solid materials that measures the tensile or compressive stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Youn ...
. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials
Strength may refer to:
Personal trait
*Physical strength, as in people or animals
*Character strengths like those listed in the Values in Action Inventory
*The exercise of willpower
Physics
* Mechanical strength, the ability to withstand ...
and for a structure by structural analysis
Structural analysis is a branch of solid mechanics which uses simplified models for solids like bars, beams and shells for engineering decision making. Its main objective is to determine the effect of loads on physical structures and their c ...
.
In the above figure, it can be seen that the compressive loading (indicated by the arrow) has caused deformation in the cylinder so that the original shape (dashed lines) has changed (deformed) into one with bulging sides. The sides bulge because the material, although strong enough to not crack or otherwise fail, is not strong enough to support the load without change. As a result, the material is forced out laterally. Internal forces (in this case at right angles to the deformation) resist the applied load.
Types of deformation
Depending on the type of material, size and geometry of the object, and the forces applied, various types of deformation may result. The image to the right shows the engineering stress vs. strain diagram for a typical ductile material such as steel. Different deformation modes may occur under different conditions, as can be depicted using a deformation mechanism map. Permanent deformation is irreversible; the deformation stays even after removal of the applied forces, while the temporary deformation is recoverable as it disappears after the removal of applied forces. Temporary deformation is also called elastic deformation, while the permanent deformation is called plastic deformation.
Elastic deformation
The study of temporary or elastic deformation in the case of engineering strain is applied to materials used in mechanical and structural engineering, such asconcrete
Concrete is a composite material composed of aggregate bound together with a fluid cement that cures to a solid over time. It is the second-most-used substance (after water), the most–widely used building material, and the most-manufactur ...
and steel
Steel is an alloy of iron and carbon that demonstrates improved mechanical properties compared to the pure form of iron. Due to steel's high Young's modulus, elastic modulus, Yield (engineering), yield strength, Fracture, fracture strength a ...
, which are subjected to very small deformations. Engineering strain is modeled by infinitesimal strain theory, also called ''small strain theory'', ''small deformation theory'', ''small displacement theory'', or ''small displacement-gradient theory'' where strains and rotations are both small.
For some materials, e.g. elastomers
An elastomer is a polymer with viscoelasticity (i.e. both viscosity and Elasticity (physics), elasticity) and with weak intermolecular forces, generally low Young's modulus (E) and high failure strain compared with other materials. The term, a ...
and polymers, subjected to large deformations, the engineering definition of strain is not applicable, e.g. typical engineering strains greater than 1%, thus other more complex definitions of strain are required, such as ''stretch'', ''logarithmic strain'', ''Green strain'', and ''Almansi strain''. Elastomer
An elastomer is a polymer with viscoelasticity (i.e. both viscosity and elasticity) and with weak intermolecular forces, generally low Young's modulus (E) and high failure strain compared with other materials. The term, a portmanteau of ''ela ...
s and shape memory metals such as Nitinol
Nickel titanium, also known as nitinol, is a metal alloy of nickel and titanium, where the two elements are present in roughly equal atomic percentages. Different alloys are named according to the weight percentage of nickel; e.g., nitinol 55 and ...
exhibit large elastic deformation ranges, as does rubber
Rubber, also called India rubber, latex, Amazonian rubber, ''caucho'', or ''caoutchouc'', as initially produced, consists of polymers of the organic compound isoprene, with minor impurities of other organic compounds.
Types of polyisoprene ...
. However, elasticity is nonlinear in these materials.
Normal metals, ceramics and most crystals show linear elasticity and a smaller elastic range.
Linear elastic deformation is governed by Hooke's law, which states:
:
where
* is the applied stress;
* is a material constant called Young's modulus
Young's modulus (or the Young modulus) is a mechanical property of solid materials that measures the tensile or compressive stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Youn ...
or elastic modulus
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it.
Definition
The elastic modu ...
;
* is the resulting strain.
This relationship only applies in the elastic range and indicates that the slope of the stress vs. strain curve can be used to find Young's modulus (). Engineers often use this calculation in tensile tests. The area under this elastic region is known as resilience.
Note that not all elastic materials undergo linear elastic deformation; some, such as concrete
Concrete is a composite material composed of aggregate bound together with a fluid cement that cures to a solid over time. It is the second-most-used substance (after water), the most–widely used building material, and the most-manufactur ...
, gray cast iron, and many polymers, respond in a nonlinear fashion. For these materials Hooke's law is inapplicable.

Plastic deformation
This type of deformation is not undone simply by removing the applied force. An object in the plastic deformation range, however, will first have undergone elastic deformation, which is undone simply by removing the applied force, so the object will return part way to its original shape. Softthermoplastics
A thermoplastic, or thermosoftening plastic, is any plastic polymer material that becomes pliable or moldable at a certain elevated temperature and solidifies upon cooling.
Most thermoplastics have a high molecular weight. The polymer chains as ...
have a rather large plastic deformation range as do ductile metals such as copper
Copper is a chemical element; it has symbol Cu (from Latin ) and atomic number 29. It is a soft, malleable, and ductile metal with very high thermal and electrical conductivity. A freshly exposed surface of pure copper has a pinkish-orang ...
, silver
Silver is a chemical element; it has Symbol (chemistry), symbol Ag () and atomic number 47. A soft, whitish-gray, lustrous transition metal, it exhibits the highest electrical conductivity, thermal conductivity, and reflectivity of any metal. ...
, and gold
Gold is a chemical element; it has chemical symbol Au (from Latin ) and atomic number 79. In its pure form, it is a brightness, bright, slightly orange-yellow, dense, soft, malleable, and ductile metal. Chemically, gold is a transition metal ...
. Steel
Steel is an alloy of iron and carbon that demonstrates improved mechanical properties compared to the pure form of iron. Due to steel's high Young's modulus, elastic modulus, Yield (engineering), yield strength, Fracture, fracture strength a ...
does, too, but not cast iron
Cast iron is a class of iron–carbon alloys with a carbon content of more than 2% and silicon content around 1–3%. Its usefulness derives from its relatively low melting temperature. The alloying elements determine the form in which its car ...
. Hard thermosetting plastics, rubber, crystals, and ceramics have minimal plastic deformation ranges. An example of a material with a large plastic deformation range is wet chewing gum
Chewing gum is a soft, cohesive substance designed to be chewed without being swallowed. Modern chewing gum is composed of gum base, sweeteners, softeners/plasticizers, flavors, colors, and, typically, a hard or powdered polyol coating. Its tex ...
, which can be stretched to dozens of times its original length.
Under tensile stress, plastic deformation is characterized by a strain hardening region and a necking region and finally, fracture (also called rupture). During strain hardening the material becomes stronger through the movement of atomic dislocations. The necking phase is indicated by a reduction in cross-sectional area of the specimen. Necking begins after the ultimate strength is reached. During necking, the material can no longer withstand the maximum stress and the strain in the specimen rapidly increases. Plastic deformation ends with the fracture of the material.
Failure
Compressive failure
Usually, compressive stress applied to bars, columns, etc. leads to shortening. Loading a structural element or specimen will increase the compressive stress until it reaches itscompressive strength
In mechanics, compressive strength (or compression strength) is the capacity of a material or Structural system, structure to withstand Structural load, loads tending to reduce size (Compression (physics), compression). It is opposed to ''tensil ...
. According to the properties of the material, failure modes are yielding for materials with ductile behavior (most metal
A metal () is a material that, when polished or fractured, shows a lustrous appearance, and conducts electrical resistivity and conductivity, electricity and thermal conductivity, heat relatively well. These properties are all associated wit ...
s, some soil
Soil, also commonly referred to as earth, is a mixture of organic matter, minerals, gases, water, and organisms that together support the life of plants and soil organisms. Some scientific definitions distinguish dirt from ''soil'' by re ...
s and plastic
Plastics are a wide range of synthetic polymers, synthetic or Semisynthesis, semisynthetic materials composed primarily of Polymer, polymers. Their defining characteristic, Plasticity (physics), plasticity, allows them to be Injection moulding ...
s) or rupturing for brittle behavior (geomaterials, cast iron
Cast iron is a class of iron–carbon alloys with a carbon content of more than 2% and silicon content around 1–3%. Its usefulness derives from its relatively low melting temperature. The alloying elements determine the form in which its car ...
, glass
Glass is an amorphous (non-crystalline solid, non-crystalline) solid. Because it is often transparency and translucency, transparent and chemically inert, glass has found widespread practical, technological, and decorative use in window pane ...
, etc.).
In long, slender structural elements — such as columns or truss
A truss is an assembly of ''members'' such as Beam (structure), beams, connected by ''nodes'', that creates a rigid structure.
In engineering, a truss is a structure that "consists of two-force members only, where the members are organized so ...
bars — an increase of compressive force ''F'' leads to structural failure due to buckling at lower stress than the compressive strength.
Fracture
A break occurs after the material has reached the end of the elastic, and then plastic, deformation ranges. At this point forces accumulate until they are sufficient to cause a fracture. All materials will eventually fracture, if sufficient forces are applied.Types of stress and strain
Engineering stress and engineering strain are approximations to the internal state that may be determined from the external forces and deformations of an object, provided that there is no significant change in size. When there is a significant change in size, the true stress and true strain can be derived from the instantaneous size of the object.Engineering stress and strain
Consider a bar of original cross sectional area being subjected to equal and opposite forces pulling at the ends so the bar is under tension. The material is experiencing a stress defined to be the ratio of the force to the cross sectional area of the bar, as well as an axial elongation: Subscript 0 denotes the original dimensions of the sample. TheSI derived unit
SI derived units are units of measurement derived from the
seven SI base units specified by the International System of Units (SI). They can be expressed as a product (or ratio) of one or more of the base units, possibly scaled by an appropriat ...
for stress is newtons per square metre, or pascals (1 pascal = 1 Pa = 1 N/m2), and strain is unitless. The stress–strain curve for this material is plotted by elongating the sample and recording the stress variation with strain until the sample fracture
Fracture is the appearance of a crack or complete separation of an object or material into two or more pieces under the action of stress (mechanics), stress. The fracture of a solid usually occurs due to the development of certain displacemen ...
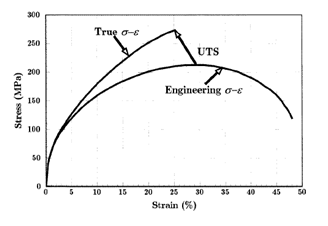
s. By convention, the strain is set to the horizontal axis and stress is set to vertical axis. Note that for engineering purposes we often assume the cross-section area of the material does not change during the whole deformation process. This is not true since the actual area will decrease while deforming due to elastic and plastic deformation. The curve based on the original cross-section and gauge length is called the ''engineering stress–strain curve'', while the curve based on the instantaneous cross-section area and length is called the ''true stress–strain curve''. Unless stated otherwise, engineering stress–strain is generally used.
True stress and strain
plastic
Plastics are a wide range of synthetic polymers, synthetic or Semisynthesis, semisynthetic materials composed primarily of Polymer, polymers. Their defining characteristic, Plasticity (physics), plasticity, allows them to be Injection moulding ...
deformation. At low strains (such as elastic
Elastic is a word often used to describe or identify certain types of elastomer, Elastic (notion), elastic used in garments or stretch fabric, stretchable fabrics.
Elastic may also refer to:
Alternative name
* Rubber band, ring-shaped band of rub ...
deformation), the differences between the two is negligible. As for the tensile strength point, it is the maximal point in engineering stress–strain curve but is not a special point in true stress–strain curve. Because engineering stress is proportional to the force applied along the sample, the criterion for necking formation can be set as
:
This analysis suggests nature of the ultimate tensile strength (UTS) point. The work strengthening effect is exactly balanced by the shrinking of section area at UTS point.
After the formation of necking, the sample undergoes heterogeneous deformation, so equations above are not valid. The stress and strain at the necking can be expressed as:
:
An empirical equation is commonly used to describe the relationship between true stress and true strain.
:
Here, is the strain-hardening exponent and is the strength coefficient. is a measure of a material's work hardening behavior. Materials with a higher have a greater resistance to necking. Typically, metals at room temperature have ranging from 0.02 to 0.5.
Discussion
Since we disregard the change of area during deformation above, the true stress and strain curve should be re-derived. For deriving the stress strain curve, we can assume that the volume change is 0 even if we deformed the materials. We can assume that: : Then, the true stress can be expressed as below: : Additionally, the true strain can be expressed as below: : Then, we can express the value as : Thus, we can induce the plot in terms of and as right figure. Additionally, based on the true stress-strain curve, we can estimate the region where necking starts to happen. Since necking starts to appear after ultimate tensile stress where the maximum force applied, we can express this situation as below: : so this form can be expressed as below: : It indicates that the necking starts to appear where reduction of area becomes much significant compared to the stress change. Then the stress will be localized to specific area where the necking appears. Additionally, we can induce various relation based on true stress-strain curve. 1) True strain and stress curve can be expressed by the approximate linear relationship by taking a log on true stress and strain. The relation can be expressed as below: : Where is stress coefficient and is strain-hardening coefficient. Usually, the value of has range around 0.02 to 0.5 at room temperature. If is 1, we can express this material as perfect elastic material. 2) In reality, stress is also highly dependent on the rate of strain variation. Thus, we can induce the empirical equation based on the strain rate variation. : Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
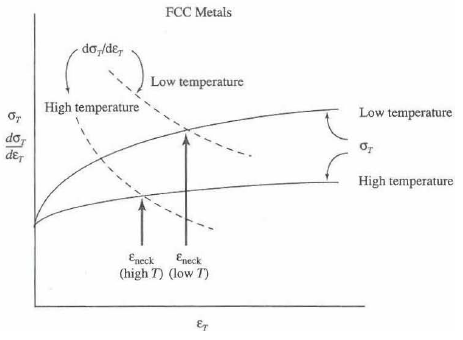
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
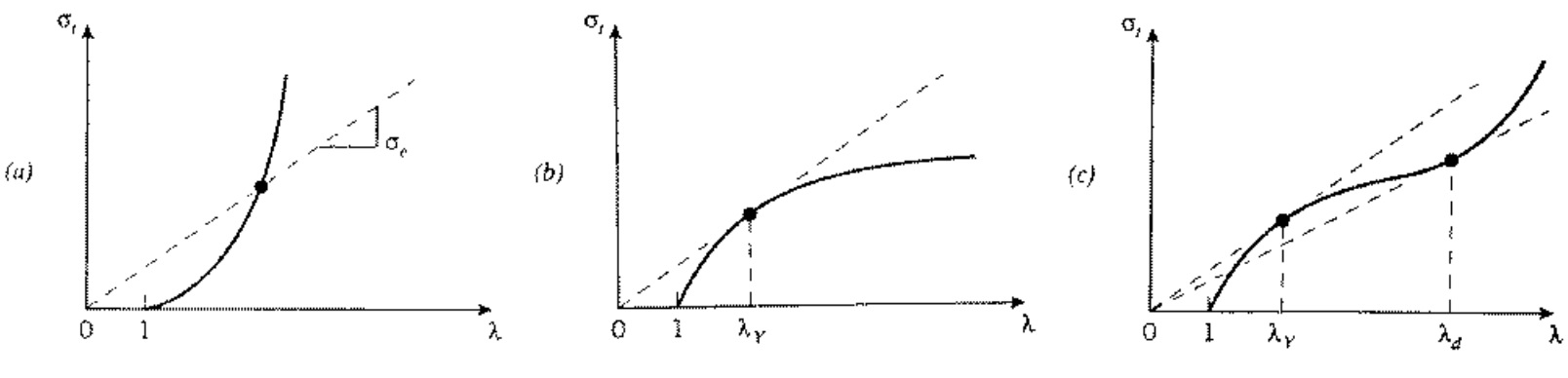
 On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
Misconceptions
A popular misconception is that all materials that bend are "weak" and those that do not are "strong". In reality, many materials that undergo large elastic and plastic deformations, such as steel, are able to absorb stresses that would cause brittle materials, such as glass, with minimal plastic deformation ranges, to break.See also
* Artificial cranial deformation * Buff strength * Creep (deformation) * Deflection (engineering) * Deformation (mechanics) * Deformation mechanism maps * Deformation monitoring * Deformation retract * Deformation theory * Elasticity *Malleability
Ductility refers to the ability of a material to sustain significant plastic Deformation (engineering), deformation before fracture. Plastic deformation is the permanent distortion of a material under applied stress, as opposed to elastic def ...
* Planar deformation features
*Plasticity (physics)
In physics and materials science, plasticity (also known as plastic deformation) is the ability of a solid material to undergo permanent Deformation (engineering), deformation, a non-reversible change of shape in response to applied forces. For ...
* Poisson's ratio
* Strain tensor
*Strength of materials
Strength may refer to:
Personal trait
*Physical strength, as in people or animals
*Character strengths like those listed in the Values in Action Inventory
*The exercise of willpower
Physics
* Mechanical strength, the ability to withstand ...
*Wood warping
Wood is a structural tissue/material found as xylem in the stems and roots of trees and other woody plants. It is an organic materiala natural composite of cellulosic fibers that are strong in tension and embedded in a matrix of lignin ...
References
{{DEFAULTSORT:Deformation (Engineering) Solid mechanics Deformation (mechanics) de:Verformung