|
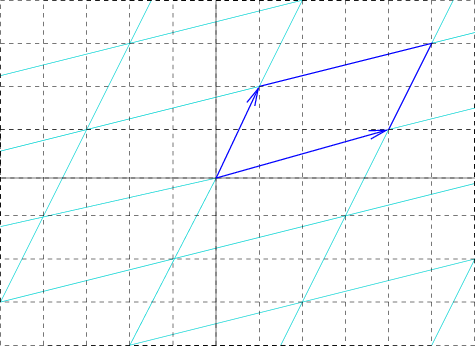
Monoclinic
In crystallography, the monoclinic crystal system is one of the seven crystal systems. A crystal system is described by three Vector (geometric), vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a parallelogram prism (geometry), prism. Hence two pairs of vectors are perpendicular (meet at right angles), while the third pair makes an angle other than 90°. Bravais lattices Two monoclinic Bravais lattices exist: the primitive monoclinic and the base-centered monoclinic. For the base-centered monoclinic lattice, the primitive cell has the shape of an oblique rhombic prism;See , row mC, column Primitive, where the cell parameters are given as a1 = a2, α = β it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. The length a of the primitive cell below equals \frac \sqrt of the conventional cell above. Crystal class ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal System
In crystallography, a crystal system is a set of point groups (a group of geometric symmetries with at least one fixed point). A lattice system is a set of Bravais lattices (an infinite array of discrete points). Space groups (symmetry groups of a configuration in space) are classified into crystal systems according to their point groups, and into lattice systems according to their Bravais lattices. Crystal systems that have space groups assigned to a common lattice system are combined into a crystal family. The seven crystal systems are ''triclinic'', ''monoclinic'', ''orthorhombic'', ''tetragonal'', ''trigonal'', ''hexagonal'', and ''cubic''. Informally, two crystals are in the same crystal system if they have similar symmetries (though there are many exceptions). Classifications Crystals can be classified in three ways: lattice systems, crystal systems and crystal families. The various classifications are often confused: in particular the trigonal crystal system i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monoclinic
In crystallography, the monoclinic crystal system is one of the seven crystal systems. A crystal system is described by three Vector (geometric), vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a parallelogram prism (geometry), prism. Hence two pairs of vectors are perpendicular (meet at right angles), while the third pair makes an angle other than 90°. Bravais lattices Two monoclinic Bravais lattices exist: the primitive monoclinic and the base-centered monoclinic. For the base-centered monoclinic lattice, the primitive cell has the shape of an oblique rhombic prism;See , row mC, column Primitive, where the cell parameters are given as a1 = a2, α = β it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. The length a of the primitive cell below equals \frac \sqrt of the conventional cell above. Crystal class ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal Structure
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter. The smallest group of particles in a material that constitutes this repeating pattern is the unit cell of the structure. The unit cell completely reflects the symmetry and structure of the entire crystal, which is built up by repetitive translation of the unit cell along its principal axes. The translation vectors define the nodes of the Bravais lattice. The lengths of principal axes/edges, of the unit cell and angles between them are lattice constants, also called ''lattice parameters'' or ''cell parameters''. The symmetry properties of a crystal are described by the concept of space groups. All possible symmetric arrangements of particles in three-dimensional space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ..., for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Group
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups. In crystallography, space groups are also called the crystallographic or Fedorov groups, and represent a description of the symmetry of the crystal. A definitive source regarding 3-dimensional space groups is the ''International Tables for Crystallography'' . History Space groups in 2 dimensions are the 17 wallpaper groups which have been known for several centuries, though the proof that the list ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primitive Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations. There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barytocalcite 1
Barytocalcite is an anhydrous barium calcium carbonate mineral with the chemical formula barium, Bacalcium, Ca(carbon, Coxygen, O3)2. It is Trimorphism, trimorphous with alstonite and paralstonite, that is to say the three minerals have the same formula but different structures. Baryte and quartz pseudomorphs after barytocalcite have been observed. Barytocalcite crystallizes in the monoclinic crystal system, typically as massive to Druse (geology), druzy accumulations of transparent white to yellow to grey aggregates of slender Prism (geometry), prismatic crystals. It has a Mohs hardness of 4 and a specific gravity of 3.64 to 3.71. It was first described in 1824 for an occurrence in the Alston Moor, Blagill Mine in North Pennines, Cumbria (Cumberland), England, and named for its composition. Structure The mineral crystallises in the monoclinic crystal system. Most sources put it in the Crystal system#Crystal classes, prismatic class 2/m, with space group P21/m, but Webmin puts it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermann–Mauguin Notation
In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann (who introduced it in 1928) and the French mineralogist Charles-Victor Mauguin (who modified it in 1931). This notation is sometimes called international notation, because it was adopted as standard by the ''International Tables For Crystallography'' since their first edition in 1935. The Hermann–Mauguin notation, compared with the Schoenflies notation, is preferred in crystallography because it can easily be used to include translational symmetry elements, and it specifies the directions of the symmetry axes. Point groups Rotation axes are denoted by a number ''n'' – 1, 2, 3, 4, 5, 6, 7, 8, ... (angle of rotation ). For improper rotations, Hermann–Mauguin symbols show rotoinversion axes, unlike Schoenflies and Shubnikov notations, that shows rotation-reflection axes. The rot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Symbol
The Pearson symbol, or Pearson notation, is used in crystallography as a means of describing a crystal structure. It was originated by William Burton Pearson and is used extensively in Pearson's handbook of crystallographic data for intermetallic phases. The symbol is made up of two letters followed by a number. For example: * Diamond structure, cF8 * Rutile structure, tP6 Construction The two letters in the Pearson symbol specify the Bravais lattice, and more specifically, the lower-case letter specifies the Crystal system, crystal family, while the upper-case letter the Lattice (group), lattice type. The number at the end of the Pearson symbol gives the number of the atoms in the conventional unit cell (atoms which satisfy 1 > x,y,z \geq 0 for the atom's position (x,y,z) in the unit cell). [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence (geometry), congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations. By comparison, a quadrilateral with at least one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The three-dimensional counterpart of a parallelogram is a parallelepiped. The word "parallelogram" comes from the Greek παραλληλό-γραμμον, ''parallēló-grammon'', which means "a shape of parallel lines". Special cases *Rectangle – A par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macroscopic single crystals are usually identifiable by their geometrical shape, consisting of flat faces with specific, characteristic orientations. The scientific study of crystals and crystal formation is known as crystallography. The process of crystal formation via mechanisms of crystal growth is called crystallization or solidification. The word ''crystal'' derives from the Ancient Greek word (), meaning both "ice" and " rock crystal", from (), "icy cold, frost". Examples of large crystals include snowflakes, diamonds, and table salt. Most inorganic solids are not crystals but polycrystals, i.e. many microscopic crystals fused together into a single solid. Polycrystals include most metals, rocks, ceramics, and ice. A third cat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |