|
Modulational Instability
In the fields of nonlinear optics and fluid dynamics, modulational instability or sideband instability is a phenomenon whereby deviations from a periodic waveform are reinforced by nonlinearity, leading to the generation of spectral-sidebands and the eventual breakup of the waveform into a train of pulses. It is widely believed that the phenomenon was first discovered − and modeled − for periodic surface gravity waves ( Stokes waves) on deep water by T. Brooke Benjamin and Jim E. Feir, in 1967. Therefore, it is also known as the Benjamin−Feir instability. However, spatial modulation instability of high-power lasers in organic solvents was observed by Russian scientists N. F. Piliptetskii and A. R. Rustamov in 1965, and the mathematical derivation of modulation instability was published by V. I. Bespalov and V. I. Talanov in 1966. Modulation instability is a possible mechanism for the generation of rogue waves. Initial instability and gain Modulation instability only happ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Optics
Nonlinear optics (NLO) is the branch of optics that describes the behaviour of light in Nonlinearity, nonlinear media, that is, media in which the polarization density P responds non-linearly to the electric field E of the light. The non-linearity is typically observed only at very high light intensities (when the electric field of the light is >108 V/m and thus comparable to the atomic electric field of ~1011 V/m) such as those provided by lasers. Above the Schwinger limit, the vacuum itself is expected to become nonlinear. In nonlinear optics, the superposition principle no longer holds. History The first nonlinear optical effect to be predicted was two-photon absorption, by Maria Goeppert Mayer for her PhD in 1931, but it remained an unexplored theoretical curiosity until 1961 and the almost simultaneous observation of two-photon absorption at Bell Labs and the discovery of second-harmonic generation by Peter Franken ''et al.'' at University of Michigan, both shortly after th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Schrödinger Equation
In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers, planar waveguides and hot rubidium vapors and to Bose–Einstein condensates confined to highly anisotropic, cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carrier Wave
In telecommunications, a carrier wave, carrier signal, or just carrier, is a periodic waveform (usually sinusoidal) that conveys information through a process called ''modulation''. One or more of the wave's properties, such as amplitude or frequency, are modified by an information bearing signal, called the ''message signal'' or ''modulation signal''. The carrier frequency is usually much higher than the message signal frequency; this is because it is usually impractical to transmit signals with low frequencies over long distances (due to attenuation). The purpose of the carrier is usually either to transmit the information through space as an electromagnetic wave (as in radio communication), or to allow several carriers at different frequencies to share a common physical transmission medium by frequency division multiplexing (as in a cable television system). The term originated in radio communication, where the carrier wave creates the waves which carry the information (mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine function (for example, in oscillations and waves). Angular frequency (or angular speed) is the magnitude of the pseudovector quantity '' angular velocity''. (UP1) Angular frequency can be obtained multiplying '' rotational frequency'', ''ν'' (or ordinary ''frequency'', ''f'') by a full turn (2 radians): . It can also be formulated as , the instantaneous rate of change of the angular displacement, ''θ'', with respect to time, ''t''. (11 pages) Unit In SI[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of reciprocal length, expressed in SI units of cycles per metre or reciprocal metre (m−1). Angular wavenumber, defined as the wave phase divided by time, is a quantity with dimension of angle per length and SI units of radians per metre. They are analogous to temporal frequency, respectively the '' ordinary frequency'', defined as the number of wave cycles divided by time (in cycles per second or reciprocal seconds), and the ''angular frequency'', defined as the phase angle divided by time (in radians per second). In multidimensional systems, the wavenumber is the magnitude of the '' wave vector''. The space of wave vectors is called ''reciprocal space''. Wave numbers and wave vectors play an essential role in optics and the physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - bi. The complex conjugate of z is often denoted as \overline or z^*. In polar form, if r and \varphi are real numbers then the conjugate of r e^ is r e^. This can be shown using Euler's formula. The product of a complex number and its conjugate is a real number: a^2 + b^2 (or r^2 in polar coordinates). If a root of a univariate polynomial with real coefficients is complex, then its complex conjugate is also a root. Notation The complex conjugate of a complex number z is written as \overline z or z^*. The first notation, a vinculum, avoids confusion with the notation for the conjugate transpose of a matrix, which can be thought of as a generalization of the complex conjugate. The second is preferred in physics, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation Theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In regular perturbation theory, the solution is expressed as a power series in a small parameter The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of \varepsilon usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, often keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction. Perturbation theory is used in a wide range of fields and reaches its most sophisticated and advanced forms in quantum field theory. Perturbation theory (quantum mechanics) describes the use of this method in quantum mechanics. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Refractive Index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refraction, refracted, when entering a material. This is described by Snell's law of refraction, , where and are the angle of incidence (optics), angle of incidence and angle of refraction, respectively, of a ray crossing the interface between two media with refractive indices and . The refractive indices also determine the amount of light that is reflectivity, reflected when reaching the interface, as well as the critical angle for total internal reflection, their intensity (Fresnel equations) and Brewster's angle. The refractive index, n, can be seen as the factor by which the speed and the wavelength of the radiation are reduced with respect to their vacuum values: the speed of light in a medium is , and similarly the wavelength in that me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
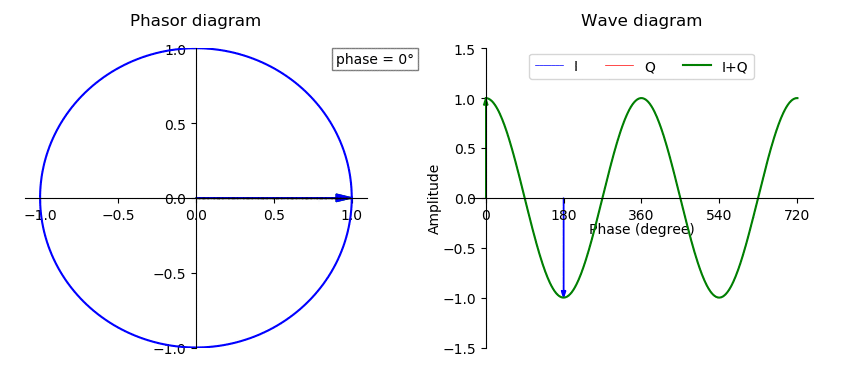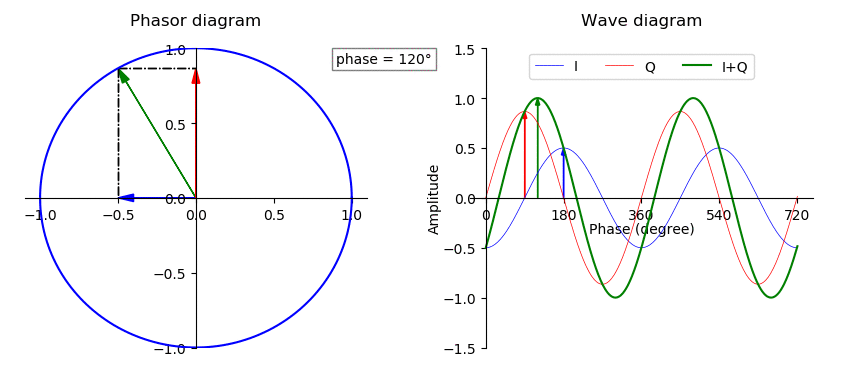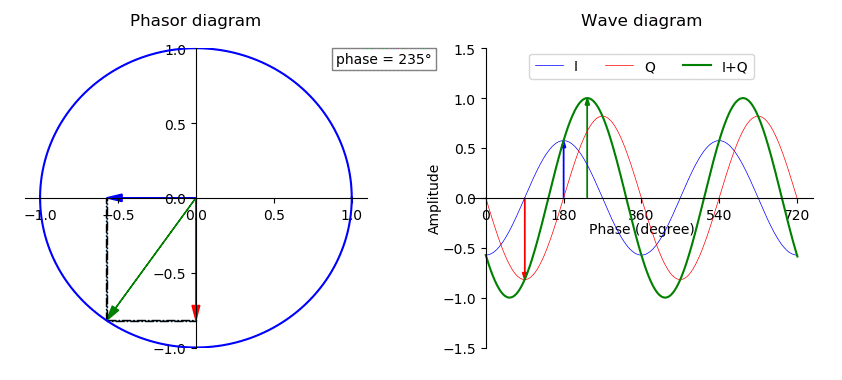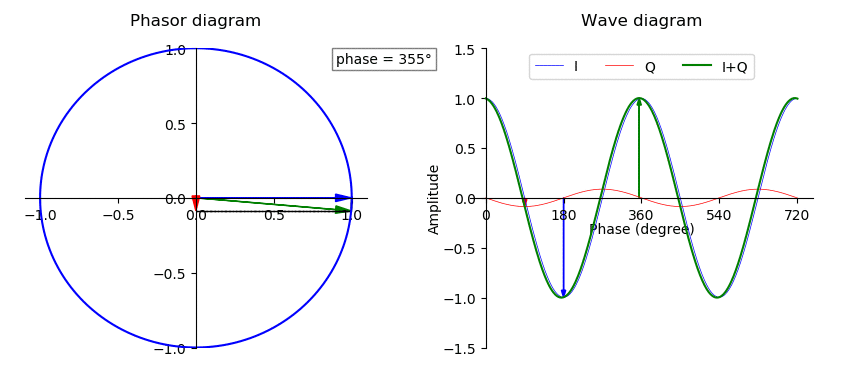
Wave Phase
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly scans ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called ''aperiodic''. Definition A function is said to be periodic if, for some nonzero constant , it is the case that :f(x+P) = f(x) for all values of in the domain. A nonzero constant for which this is the case is called a period of the function. If there exists a least positive constant with this property, it is called the fundamental period (also primitive period, basic period, or prime period.) Often, "the" period of a function is used to mean its fundamental period. A funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerr Effect
The Kerr effect, also called the quadratic electro-optic (QEO) effect, is a change in the refractive index of a material in response to an applied electric field. The Kerr effect is distinct from the Pockels effect in that the induced index change for the Kerr effect is directly proportional to the ''square'' of the electric field instead of varying linearly with it. All materials show a Kerr effect, but certain liquids display it more strongly than others. The Kerr effect was discovered in 1875 by Scottish physicist John Kerr. Two special cases of the Kerr effect are normally considered, these being the Kerr electro-optic effect, or DC Kerr effect, and the optical Kerr effect, or AC Kerr effect. Kerr electro-optic effect The Kerr electro-optic effect, or DC Kerr effect, is the special case in which a slowly varying external electric field is applied by, for instance, a voltage on electrodes across the sample material. Under this influence, the sample becomes birefringent, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |