|
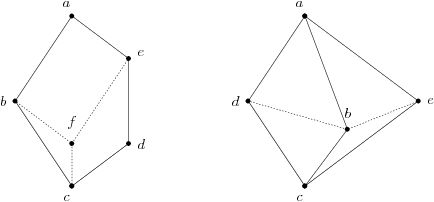
Modular Graph
In graph theory, a branch of mathematics, the modular graphs are undirected graphs in which every three vertices , , and have at least one ''median vertex'' that belongs to shortest paths between each pair of , , and .Modular graphs Information System on Graph Classes and their Inclusions, retrieved 2016-09-30. Their name comes from the fact that a finite lattice is a if and only if its is a modular graph.. It is not possible for a modu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2d Modular Lattice
D, or d, is the fourth Letter (alphabet), letter of the Latin alphabet, used in the English alphabet, modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is English alphabet#Letter names, ''dee'' (pronounced ), plural ''dees''. History The Semitic languages, Semitic letter Daleth, Dāleth may have developed from the logogram for a fish or a door. There are many different Egyptian hieroglyphs that might have inspired this. In Semitic, Ancient Greek and Latin, the letter represented ; in the Etruscan alphabet the letter was archaic but still retained. The equivalent Greek letter is delta, Delta (letter), Δ. The lower case, minuscule (lower-case) form of 'd' consists of a lower-story left Typeface anatomy#Strokes, bowl and a Typeface anatomy#Strokes, stem ascender. It most likely developed by gradual variations on the upper case, majuscule (capital) form 'D', and is now composed as a stem with a full Typeface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') which are connected by ''Glossary of graph theory terms#edge, edges'' (also called ''arcs'', ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a Set (mathematics), set of vertices (also called nodes or points); * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undirected Graph
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called '' vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', then this graph is directed, because owing money is not necessarily reciprocated. Gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex (graph Theory)
In discrete mathematics, and more specifically in graph theory, a vertex (plural vertices) or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another. From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network is a graph in which the vertices represent concepts or classes of objects. The two vertices forming an edge are said to be the endpoints of this edge, and the edge is said to be incident to the vertices. A vertex ''w'' is said to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shortest Path
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized. The problem of finding the shortest path between two intersections on a road map may be modeled as a special case of the shortest path problem in graphs, where the vertices correspond to intersections and the edges correspond to road segments, each weighted by the length or distance of each segment. Definition The shortest path problem can be defined for graphs whether undirected, directed, or mixed. The definition for undirected graphs states that every edge can be traversed in either direction. Directed graphs require that consecutive vertices be connected by an appropriate directed edge. Two vertices are adjacent when they are both incident to a common edge. A path in an undirected graph is a sequence of vertices P = ( v_1, v_2, \ldots, v_n ) \in V \times V \times \cdots \times V suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (order)
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum (also called a least upper bound or join (mathematics), join) and a unique infimum (also called a greatest lower bound or meet (mathematics), meet). An example is given by the power set of a set, partially ordered by Subset, inclusion, for which the supremum is the Union (set theory), union and the infimum is the Intersection (set theory), intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor. Lattices can also be characterized as algebraic structures satisfying certain axiomatic Identity (mathematics), identities. Since the two definitions are equivalent, lattice theory draws on both order theory and universal algebra. Semilatti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Lattice
In the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self- dual condition, ;Modular law: implies where are arbitrary elements in the lattice, ≤ is the partial order, and ∨ and ∧ (called join and meet respectively) are the operations of the lattice. This phrasing emphasizes an interpretation in terms of projection onto the sublattice , a fact known as the diamond isomorphism theorem. An alternative but equivalent condition stated as an equation (see below) emphasizes that modular lattices form a variety in the sense of universal algebra. Modular lattices arise naturally in algebra and in many other areas of mathematics. In these scenarios, modularity is an abstraction of the 2nd Isomorphism Theorem. For example, the subspaces of a vector space (and more generally the submodules of a module over a ring) form a modular lattice. In a not necessarily modular lattice, there may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hasse Diagram
In order theory, a Hasse diagram (; ) is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set (S,\le) one represents each element of S as a vertex in the plane and draws a line segment or curve that goes ''upward'' from one vertex x to another vertex y whenever y covers x (that is, whenever x\ne y, x\le y and there is no z distinct from x and y with x\le z\le y). These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order. Hasse diagrams are named after Helmut Hasse (1898–1979); according to Garrett Birkhoff, they are so called because of the effective use Hasse made of them. However, Hasse was not the first to use these diagrams. One example that predates Hasse can be found in an 1895 work by Henri Gustave Vogt. Although Hasse diagrams were orig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Applied Mathematics
''Discrete Applied Mathematics'' is a peer-reviewed scientific journal covering algorithmic and applied areas of discrete mathematics. It is published by Elsevier and the editor-in-chief is Endre Boros (Rutgers University). The journal was split off from another Elsevier journal, ''Discrete Mathematics'', in 1979, with that journal's founder Peter Ladislaw Hammer as its founding editor-in-chief. Abstracting and indexing The journal is abstracted and indexing in: According to the ''Journal Citation Reports'', the journal has a 2020 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 1.139. References External links *{{official website, http://www.journals.elsevier.com/discrete-applied-mathematics/ Discrete mathematics journals Academic journals established in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipartite Graph
In the mathematics, mathematical field of graph theory, a bipartite graph (or bigraph) is a Graph (discrete mathematics), graph whose vertex (graph theory), vertices can be divided into two disjoint sets, disjoint and Independent set (graph theory), independent sets U and V, that is, every edge (graph theory), edge connects a Vertex (graph theory), vertex in U to one in V. Vertex sets U and V are usually called the ''parts'' of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycle (graph theory), cycles. The two sets U and V may be thought of as a graph coloring, coloring of the graph with two colors: if one colors all nodes in U blue, and all nodes in V red, each edge has endpoints of differing colors, as is required in the graph coloring problem.. In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a Gallery of named graphs, triangle: after one node is colored blue and another red, the third vertex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median Graph
In graph theory, a division of mathematics, a median graph is an undirected graph in which every three vertex (graph theory), vertices ''a'', ''b'', and ''c'' have a unique ''median'': a vertex ''m''(''a'',''b'',''c'') that belongs to shortest paths between each pair of ''a'', ''b'', and ''c''. The concept of median graphs has long been studied, for instance by or (more explicitly) by , but the first paper to call them "median graphs" appears to be . As Fan Chung, Chung, Ronald Graham, Graham, and Saks write, "median graphs arise naturally in the study of ordered sets and discrete distributive lattices, and have an extensive literature".. In phylogenetics, the Buneman graph representing all maximum parsimony Phylogenetic tree, evolutionary trees is a median graph. Median graphs also arise in social choice theory: if a set of alternatives has the structure of a median graph, it is possible to derive in an unambiguous way a majority preference among them. Additional surveys of m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributive Lattice
In mathematics, a distributive lattice is a lattice (order), lattice in which the operations of join and meet distributivity, distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union (set theory), union and intersection (set theory), intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to order isomorphism, isomorphism—given as such a lattice of sets. Definition As in the case of arbitrary lattices, one can choose to consider a distributive lattice ''L'' either as a structure of order theory or of universal algebra. Both views and their mutual correspondence are discussed in the article on lattice (order), lattices. In the present situation, the algebraic description appears to be more convenient. A lattice (''L'',∨,∧) is distributive if the following additional identity holds for all ''x'', ''y'', and ''z'' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |