|
Midsquare Quadrilateral
In elementary geometry, a quadrilateral whose diagonals are perpendicular and of equal length has been called a midsquare quadrilateral (referring to the square formed by its four edge midpoints). These shapes are, by definition, simultaneously equidiagonal quadrilaterals and orthodiagonal quadrilaterals. Older names for the same shape include pseudo-square, and skewsquare. Midsquare In any quadrilateral, the four edge midpoints form a parallelogram, the Varignon parallelogram, whose sides are parallel to the diagonals and half their length. It follows that, in an equidiagonal and orthodiagonal quadrilateral, the sides of the Varignon parallelogram are equal-length and perpendicular; that is, it is a square. For the same reason, a quadrilateral whose Varignon parallelogram is square must be equidiagonal and orthodiagonal. This characterization motivates the midsquare quadrilateral name for these shapes. A midsquare quadrilateral can be constructed from its midsquare and any one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biggest Little Polygon
In geometry, the biggest little polygon for a number n is the n-sided polygon that has diameter one (that is, every two of its points are within unit distance of each other) and that has the largest area among all diameter-one n-gons. One non-unique solution when n=4 is a square, and the solution is a regular polygon when n is an odd number, but the solution is irregular otherwise. Quadrilaterals For n=4, the area of an arbitrary quadrilateral is given by the formula S=\tfrac12pq\sin\theta where p and q are the two diagonals of the quadrilateral and \theta is either of the angles they form with each other. In order for the diameter to be at most one, both p and q must themselves be at most one. Therefore, the quadrilateral has largest area when the three factors in the area formula are individually maximized, with p=q=1 and \sin\theta=1. The condition that p=q means that the quadrilateral is an equidiagonal quadrilateral (its diagonals have equal length), and the condition that \s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Mathematical Gazette
''The Mathematical Gazette'' is a triannual peer-reviewed academic journal published by Cambridge University Press on behalf of the Mathematical Association. It covers mathematics education with a focus on the 15–20 years age range. The journal was established in 1894 by Edward Mann Langley as the successor to the ''Reports of the Association for the Improvement of Geometrical Teaching''. William John Greenstreet was its editor-in-chief for more than thirty years (1897–1930). Since 2000, the editor is Gerry Leversha. Editors-in-chief The following persons are or have been editor-in-chief: Abstracting and indexing The journal is abstracted and indexed in EBSCO databases, Emerging Sources Citation Index, Scopus Scopus is a scientific abstract and citation database, launched by the academic publisher Elsevier as a competitor to older Web of Science in 2004. The ensuing competition between the two databases has been characterized as "intense" and is c ..., and zbMA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commentarii Mathematici Helvetici
The ''Commentarii Mathematici Helvetici'' is a quarterly peer-reviewed scientific journal in mathematics. The Swiss Mathematical Society (SMG) started the journal in 1929 after a meeting in May of the previous year. The Swiss Mathematical Society still owns and operates the journal; the publishing is currently handled on its behalf by the European Mathematical Society. The scope of the journal includes research articles in all aspects in mathematics. The editors-in-chief have been Rudolf Fueter (1929–1949), J.J. Burckhardt (1950–1981), P. Gabriel (1982–1989), H. Kraft (1990–2005), and Eva Bayer-Fluckiger (2006–present). Abstracting and indexing The journal is abstracted and indexed in: According to the ''Journal Citation Reports'', the journal has a 2019 impact factor of 0.854. History The idea for a society-owned research journal emerged in June 1926, when the SMG petitioned the Swiss Confederation for a CHF 3,500 subsidy "to establish its own scientific jour ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The American Mathematical Monthly
''The American Mathematical Monthly'' is a peer-reviewed scientific journal of mathematics. It was established by Benjamin Finkel in 1894 and is published by Taylor & Francis on behalf of the Mathematical Association of America. It is an expository journal intended for a wide audience of mathematicians, from undergraduate students to research professionals. Articles are chosen on the basis of their broad interest and reviewed and edited for quality of exposition as well as content. The editor-in-chief is Vadim Ponomarenko (San Diego State University). The journal gives the Lester R. Ford Award annually to "authors of articles of expository excellence" published in the journal. Editors-in-chief The following persons are or have been editor-in-chief: See also *''Mathematics Magazine'' *''Notices of the American Mathematical Society ''Notices of the American Mathematical Society'' is the membership journal of the American Mathematical Society (AMS), published monthly except f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Combinatorial Theory, Series A
The ''Journal of Combinatorial Theory'', Series A and Series B, are mathematical journals specializing in combinatorics and related areas. They are published by Elsevier. ''Series A'' is concerned primarily with structures, designs, and applications of combinatorics. ''Series B'' is concerned primarily with graph and matroid theory. The two series are two of the leading journals in the field and are widely known as ''JCTA'' and ''JCTB''. The journal was founded in 1966 by Frank Harary and Gian-Carlo Rota.They are acknowledged on the journals' title pages and Web sites. SeEditorial board of JCTA Originally there was only one journal, which was split into two parts in 1971 as the field grew rapidly. In 2020, most of the editorial board of ''JCTA'' resigned to form a new, |
Elemente Der Mathematik
''Elemente der Mathematik'' is a peer-reviewed scientific journal covering mathematics. It is published by the European Mathematical Society Publishing House on behalf of the Swiss Mathematical Society. It was established in 1946 by Louis Locher-Ernst, and transferred to the Swiss Mathematical Society in 1976. Rather than publishing research papers, it focuses on survey papers aimed at a broad audience. History The journal ''Elemente der Mathematik'' was founded in 1946 by Louis Locher-Ernst under the patronage of the Swiss Mathematical Society (SMG) to disseminate pedagogical and expository articles in mathematics and physics. Locher-Ernst outlined the scope and objectives—emphasising support for secondary and tertiary instruction—in a letter to the SMG president in August 1945 and at the autumn members' meeting in Fribourg later that year. Early editorial responsibilities were assumed by Locher-Ernst alongside Erwin Voellmy, Ernst Trost and Paul Buchner, while an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence (geometry), congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations. By comparison, a quadrilateral with at least one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The three-dimensional counterpart of a parallelogram is a parallelepiped. The word "parallelogram" comes from the Greek παραλληλό-γραμμον, ''parallēló-grammon'', which means "a shape of parallel lines". Special cases *Rectangle – A par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kite (geometry)
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word ''deltoid'' may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.See H. S. M. Coxeter's review of in : "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid." A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombus, rhombi, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
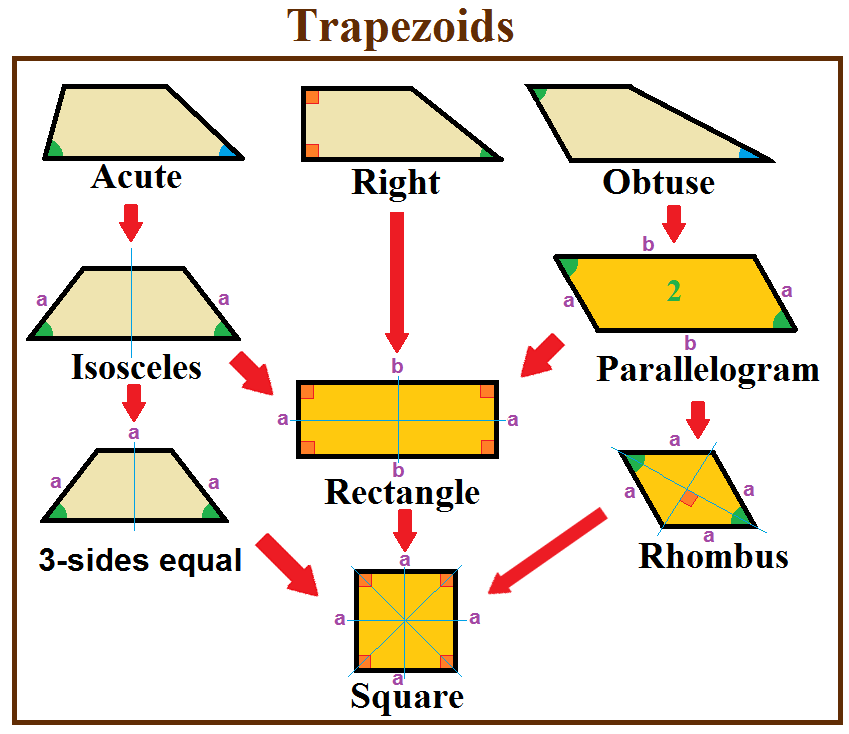
Trapezoid
In geometry, a trapezoid () in North American English, or trapezium () in British English, is a quadrilateral that has at least one pair of parallel sides. The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' or ''lateral sides''. (If the trapezoid is a parallelogram, then the choice of bases and legs is arbitrary.) A trapezoid is usually considered to be a convex quadrilateral in Euclidean geometry, but there are also crossed cases. If ''ABCD'' is a convex trapezoid, then ''ABDC'' is a crossed trapezoid. The metric formulas in this article apply in convex trapezoids. Definitions ''Trapezoid'' can be defined exclusively or inclusively. Under an exclusive definition a trapezoid is a quadrilateral having pair of parallel sides, with the other pair of opposite sides non-parallel. Parallelograms including rhombi, rectangles, and squares are then not considered to be trapezoids. Under an inclusive definition, a trapezoid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diameter Of A Set
In mathematics, the diameter of a set of points in a metric space is the largest distance between points in the set. As an important special case, the diameter of a metric space is the largest distance between any two points in the space. This generalizes the diameter of a circle, the largest distance between two points on the circle. This usage of diameter also occurs in medical terminology concerning a lesion or in geology concerning a rock. A bounded set is a set whose diameter is finite. Within a bounded set, all distances are at most the diameter. Formal definition The diameter of an object is the least upper bound (denoted "sup") of the set of all distances between pairs of points in the object. Explicitly, if S is a set of points with distances measured by a Metric (mathematics), metric \rho, the diameter is \operatorname(S) = \sup_ \rho(x, y). Of the empty set The diameter of the empty set is a matter of convention. It can be defined to be zero, -\infty, or undefined. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple polygon, simple (not self-intersecting), or complex polygon, complex (self-intersecting, or crossed). Simple quadrilaterals are either convex polygon, convex or concave polygon, concave. The Internal and external angle, interior angles of a simple (and Plane (geometry), planar) quadrilateral ''ABCD'' add up to 360 Degree (angle), degrees, that is :\angle A+\angle B+\angle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |