|
Metric Learning
Similarity learning is an area of supervised machine learning in artificial intelligence. It is closely related to regression and classification, but the goal is to learn a similarity function that measures how similar or related two objects are. It has applications in ranking, in recommendation systems, visual identity tracking, face verification, and speaker verification. Learning setup There are four common setups for similarity and metric distance learning. ; ''Regression similarity learning'' : In this setup, pairs of objects are given (x_i^1, x_i^2) together with a measure of their similarity y_i \in R . The goal is to learn a function that approximates f(x_i^1, x_i^2) \sim y_i for every new labeled triplet example (x_i^1, x_i^2, y_i). This is typically achieved by minimizing a regularized loss \min_W \sum_i loss(w;x_i^1, x_i^2,y_i) + reg(w). ; ''Classification similarity learning'' : Given are pairs of similar objects (x_i, x_i^+) and non similar objects (x_i, x_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Supervised Learning
In machine learning, supervised learning (SL) is a paradigm where a Statistical model, model is trained using input objects (e.g. a vector of predictor variables) and desired output values (also known as a ''supervisory signal''), which are often human-made labels. The training process builds a function that maps new data to expected output values. An optimal scenario will allow for the algorithm to accurately determine output values for unseen instances. This requires the learning algorithm to Generalization (learning), generalize from the training data to unseen situations in a reasonable way (see inductive bias). This statistical quality of an algorithm is measured via a ''generalization error''. Steps to follow To solve a given problem of supervised learning, the following steps must be performed: # Determine the type of training samples. Before doing anything else, the user should decide what kind of data is to be used as a Training, validation, and test data sets, trainin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Metric (mathematics)
In mathematics, a metric space is a set together with a notion of ''distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are a general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different branches of mathematics. Many types of mathematical objects have a natural notion of distance and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
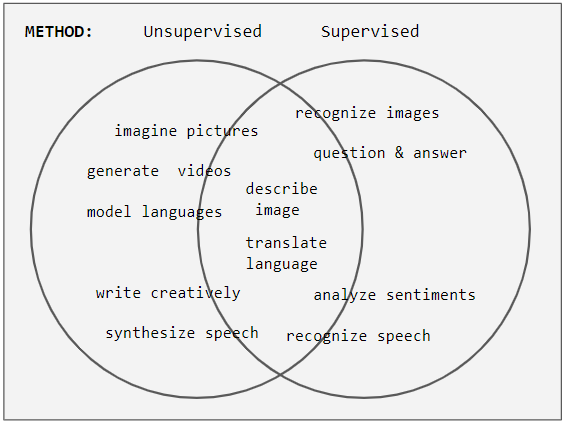 |
Unsupervised Learning
Unsupervised learning is a framework in machine learning where, in contrast to supervised learning, algorithms learn patterns exclusively from unlabeled data. Other frameworks in the spectrum of supervisions include weak- or semi-supervision, where a small portion of the data is tagged, and self-supervision. Some researchers consider self-supervised learning a form of unsupervised learning. Conceptually, unsupervised learning divides into the aspects of data, training, algorithm, and downstream applications. Typically, the dataset is harvested cheaply "in the wild", such as massive text corpus obtained by web crawling, with only minor filtering (such as Common Crawl). This compares favorably to supervised learning, where the dataset (such as the ImageNet1000) is typically constructed manually, which is much more expensive. There were algorithms designed specifically for unsupervised learning, such as clustering algorithms like k-means, dimensionality reduction techniques l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Learning To Rank
Learning to rank. Slides from Tie-Yan Liu's talk at World Wide Web Conference, WWW 2009 conference aravailable online or machine-learned ranking (MLR) is the application of machine learning, typically Supervised learning, supervised, Semi-supervised learning, semi-supervised or reinforcement learning, in the construction of ranking function, ranking models for information retrieval systems. Training data may, for example, consist of lists of items with some partial order specified between items in each list. This order is typically induced by giving a numerical or ordinal score or a binary judgment (e.g. "relevant" or "not relevant") for each item. The goal of constructing the ranking model is to rank new, unseen lists in a similar way to rankings in the training data. Applications In information retrieval Ranking is a central part of many information retrieval problems, such as document retrieval, collaborative filtering, sentiment analysis, and online advertising. A possi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Mahalanobis Distance
The Mahalanobis distance is a distance measure, measure of the distance between a point P and a probability distribution D, introduced by Prasanta Chandra Mahalanobis, P. C. Mahalanobis in 1936. The mathematical details of Mahalanobis distance first appeared in the ''Journal of The Asiatic Society of Bengal'' in 1936. Mahalanobis's definition was prompted by the problem of similarity measure, identifying the similarities of skulls based on measurements (the earliest work related to similarities of skulls are from 1922 and another later work is from 1927). Raj Chandra Bose, R.C. Bose later obtained the sampling distribution of Mahalanobis distance, under the assumption of equal dispersion. It is a multivariate generalization of the square of the standard score z=(x- \mu)/\sigma: how many standard deviations away P is from the mean of D. This distance is zero for P at the mean of D and grows as P moves away from the mean along each principal component axis. If each of these axes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one variable mainly correspond with greater values of the other variable, and the same holds for lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when greater values of one variable mainly correspond to lesser values of the other (that is, the variables tend to show opposite behavior), the covariance is negative. The magnitude of the covariance is the geometric mean of the variances that are in common for the two random variables. The Pearson product-moment correlation coefficient, correlation coefficient normalizes the covariance by dividing by the geometric mean of the total variances for the two random variables. A distinction must be made between (1) the covariance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Large Margin Nearest Neighbor
Large margin nearest neighbor (LMNN) classification is a statistical machine learning algorithm for similarity learning, metric learning. It learns a Pseudometric space, pseudometric designed for k-nearest neighbor classification. The algorithm is based on semidefinite programming, a sub-class of convex optimization. The goal of supervised learning (more specifically classification) is to learn a decision rule that can categorize data instances into pre-defined classes. The k-nearest neighbor rule assumes a ''training'' data set of labeled instances (i.e. the classes are known). It classifies a new data instance with the class obtained from the majority vote of the k closest (labeled) training instances. Closeness is measured with a pre-defined metric (mathematics), metric. Large margin nearest neighbors is an algorithm that learns this global (pseudo-)metric in a supervised fashion to improve the classification accuracy of the k-nearest neighbor rule. Setup The main intuition be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Triplet Loss
A triplet is a set of three items. It may refer to: Science * A series of three nucleotide bases forming an element of the Genetic code * J-coupling as part of Nuclear magnetic resonance spectroscopy * Opal in preparation to be a gemstone * Spin triplet in quantum mechanics, as in triplet oxygen, or triplet state in general * Tuple of length 3 in mathematics Technologies * Photography triplet, or paint triplet * Triplet lens, an optical device consisting of three single lenses * Tandem bicycle, with three seats Other uses * Triplets, the multiple birth of three children * Triplet Lakes, a group of lakes in Minnesota * ''The Triplets'', a Spanish children's book * The Triplets (band), a Latin pop group * Binghamton Triplets, a minor league baseball team * A triplet, a kind of assembled gem * In music, a tuplet of three successive notes of equal duration * "The Triplets", Tyler Johnson, Ondrej Palat, and Nikita Kucherov of the 2014–15 Tampa Bay Lightning See also * * Triplett ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Feature Vector
In machine learning and pattern recognition, a feature is an individual measurable property or characteristic of a data set. Choosing informative, discriminating, and independent features is crucial to produce effective algorithms for pattern recognition, classification, and regression tasks. Features are usually numeric, but other types such as strings and graphs are used in syntactic pattern recognition, after some pre-processing step such as one-hot encoding. The concept of "features" is related to that of explanatory variables used in statistical techniques such as linear regression. Feature types In feature engineering, two types of features are commonly used: numerical and categorical. Numerical features are continuous values that can be measured on a scale. Examples of numerical features include age, height, weight, and income. Numerical features can be used in machine learning algorithms directly. Categorical features are discrete values that can be grouped into c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Subadditivity
In mathematics, subadditivity is a property of a function that states, roughly, that evaluating the function for the sum of two elements of the domain always returns something less than or equal to the sum of the function's values at each element. There are numerous examples of subadditive functions in various areas of mathematics, particularly norms and square roots. Additive maps are special cases of subadditive functions. Definitions A subadditive function is a function f \colon A \to B, having a domain ''A'' and an ordered codomain ''B'' that are both closed under addition, with the following property: \forall x, y \in A, f(x+y)\leq f(x)+f(y). An example is the square root function, having the non-negative real numbers as domain and codomain: since \forall x, y \geq 0 we have: \sqrt\leq \sqrt+\sqrt. A sequence \left \_ is called subadditive if it satisfies the inequality a_\leq a_n+a_m for all ''m'' and ''n''. This is a special case of subadditive function, if a sequ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant under some Transformation (function), transformations, such as Translation (geometry), translation, Reflection (mathematics), reflection, Rotation (mathematics), rotation, or Scaling (geometry), scaling. Although these two meanings of the word can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a space, spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including scientific model, theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |