|
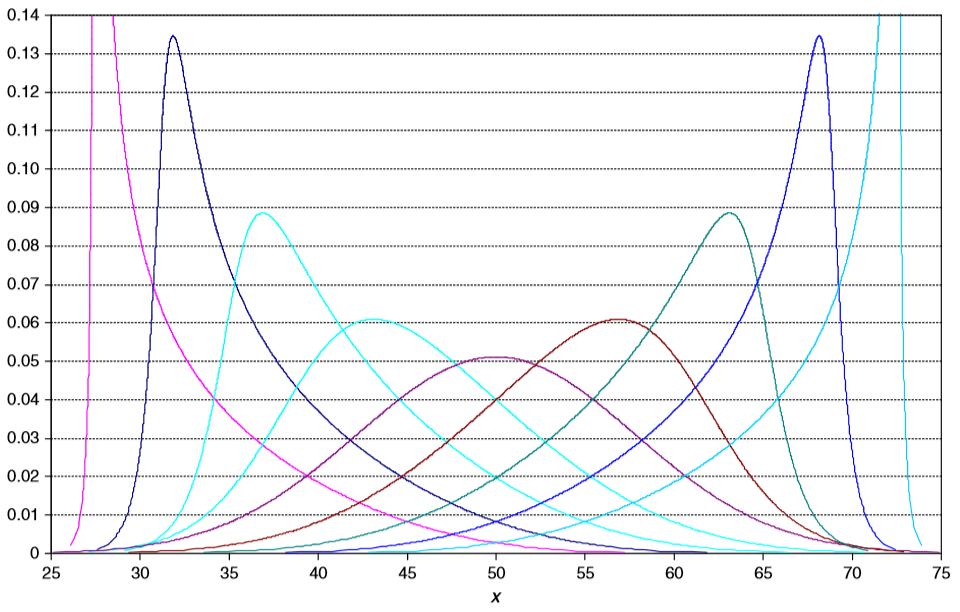
Metalog Distribution
The metalog distribution is a flexible continuous probability distribution designed for ease of use in practice. Together with its transforms, the metalog family of continuous distributions is unique because it embodies ''all'' of following properties: virtually unlimited shape flexibility; a choice among unbounded, semi-bounded, and bounded distributions; ease of fitting to data with linear least squares; simple, closed-form quantile function (inverse Cumulative distribution function, CDF) equations that facilitate Inverse transform sampling, simulation; a simple, closed-form Probability density function, PDF; and Bayesian updating in closed form in light of new data. Moreover, like a Taylor series, metalog distributions may have any number of terms, depending on the degree of shape flexibility desired and other application needs. Applications where metalog distributions can be useful typically involve fitting empirical data, simulated data, or Expert elicitation, expert-elicited ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
STP Metalog
STP may refer to: Places * São Tomé and Príncipe (ISO 3166-1 alpha-3 code, IOC country code, and FIFA country code STP) * St Pancras railway station (National Rail code STP) * St. Paul Downtown Airport (IATA airport code STP) in Saint Paul, Minnesota, US * South Texas Nuclear Generating Station, also known as the South Texas Project Businesses and organizations * German Union of Saddlers, Upholsterers and Portfolio Makers, a former German trade union * STP (motor oil company) * Segmenting-targeting-positioning, a framework in marketing * Society for Threatened Peoples, an international NGO * Space Test Program, a spaceflight provider for US DoD * Straight-through processing, in securities transaction * Suntech Power (NYSE symbol STP) Drugs * 2,5-Dimethoxy-4-methylamphetamine, also called DOM or "serenity, tranquility, and peace" Entertainment * Star Trek: Picard (2020 TV series), an American science fiction TV series * Star Trek: Prodigy (2021 TV series), an American sci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Uniform Distribution
In probability theory and statistics, the continuous uniform distributions or rectangular distributions are a family of symmetric probability distributions. Such a distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds. The bounds are defined by the parameters, a and b, which are the minimum and maximum values. The interval can either be closed (i.e. ,b/math>) or open (i.e. (a,b)). Therefore, the distribution is often abbreviated U(a,b), where U stands for uniform distribution. The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable X under no constraint other than that it is contained in the distribution's support. Definitions Probability density function The probability density function of the continuous uniform distribution is f(x) = \begin \dfrac & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A model with exactly one explanatory variable is a ''simple linear regression''; a model with two or more explanatory variables is a multiple linear regression. This term is distinct from multivariate linear regression, which predicts multiple correlated dependent variables rather than a single dependent variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimation theory, estimated from the data. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Least Squares
Linear least squares (LLS) is the least squares approximation of linear functions to data. It is a set of formulations for solving statistical problems involved in linear regression, including variants for ordinary (unweighted), weighted, and generalized (correlated) residuals. Numerical methods for linear least squares include inverting the matrix of the normal equations and orthogonal decomposition methods. Basic formulation Consider the linear equation where A \in \mathbb^ and b \in \mathbb^m are given and x \in \mathbb^n is variable to be computed. When m > n, it is generally the case that () has no solution. For example, there is no value of x that satisfies \begin 1 & 0 \\ 0 & 1 \\ 1 & 1 \end x = \begin 1 \\ 1 \\ 0 \end, because the first two rows require that x = (1, 1), but then the third row is not satisfied. Thus, for m > n, the goal of solving () exactly is typically replaced by finding the value of x that minimizes some error. There are many ways th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution Support (measure theory), supported on the real numbers, discrete or "mixed" as well as Continuous variable, continuous, is uniquely identified by a right-continuous Monotonic function, monotone increasing function (a càdlàg function) F \colon \mathbb R \rightarrow [0,1] satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from negative infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decision Analysis
Decision analysis (DA) is the Academic discipline, discipline comprising the philosophy, methodology, and professional practice necessary to address important Decision making, decisions in a formal manner. Decision analysis includes many procedures, methods, and tools for identifying, clearly representing, and formally assessing important aspects of a decision; for prescribing a recommended course of action by applying the maximum Expected_utility_hypothesis, expected-utility action axiom, axiom to a well-formed representation of the decision; and for translating the formal representation of a decision and its corresponding recommendation into insight for the Decision making, decision maker, and other corporate and non-corporate Stakeholder (corporate), stakeholders. History In 1931, mathematical philosopher Frank_Ramsey_(mathematician), Frank Ramsey pioneered the idea of Probability_interpretations#Subjectivism, subjective probability as a Expected utility hypothesis#Ramsey-theore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kurtosis
In probability theory and statistics, kurtosis (from , ''kyrtos'' or ''kurtos'', meaning "curved, arching") refers to the degree of “tailedness” in the probability distribution of a real-valued random variable. Similar to skewness, kurtosis provides insight into specific characteristics of a distribution. Various methods exist for quantifying kurtosis in theoretical distributions, and corresponding techniques allow estimation based on sample data from a population. It’s important to note that different measures of kurtosis can yield varying interpretations. The standard measure of a distribution's kurtosis, originating with Karl Pearson, is a scaled version of the fourth moment of the distribution. This number is related to the tails of the distribution, not its peak; hence, the sometimes-seen characterization of kurtosis as " peakedness" is incorrect. For this measure, higher kurtosis corresponds to greater extremity of deviations (or outliers), and not the configur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For a unimodal distribution (a distribution with a single peak), negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value in skewness means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat. Thus, the judgement on the symmetry of a given distribution by using only its skewness is risky; the distribution shape must be taken into account. Introduction Consider the two d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose. The ''arithmetic mean'', also known as "arithmetic average", is the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the numbers are from observing a sample of a larger group, the arithmetic mean is termed the '' sample mean'' (\bar) to distinguish it from the group mean (or expected value) of the underlying distribution, denoted \mu or \mu_x. Outside probability and statistics, a wide rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norman Lloyd Johnson
Norman Lloyd Johnson (9 January 1917, Ilford, Essex, England – 18 November 2004, Chapel Hill, North Carolina, United States) was a professor of statistics and author or editor of several standard reference works in statistics and probability theory. Education Johnson attended Ilford County High School, and went on to University College London, where he obtained a B.Sc. in mathematics 1936 and a B.Sc. and M.Sc. in statistics in 1937 and 1938. Career On qualification in 1938, Johnson was appointed Assistant Lecturer in the Department of Statistics at UCL. During World War II, he served under his former Professor Egon Pearson as an Experimental Officer with the Ordnance Board. He returned to the Statistics Department at UCL in 1945 and stayed there until 1962, as Assistant Lecturer, Lecturer and then Reader. In 1948 he was awarded a Ph.D. in Statistics for his work on the Johnson system of frequency curves. In 1949 he became a Fellow of the Institute of Actuaries. Two vi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F Distribution
In probability theory and statistics, the ''F''-distribution or ''F''-ratio, also known as Snedecor's ''F'' distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor), is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other ''F''-tests. Definitions The ''F''-distribution with ''d''1 and ''d''2 degrees of freedom is the distribution of X = \frac where U_1 and U_2 are independent random variables with chi-square distributions with respective degrees of freedom d_1 and d_2. It can be shown to follow that the probability density function (pdf) for ''X'' is given by \begin f(x; d_1,d_2) &= \frac \\ pt&=\frac \left(\frac\right)^ x^ \left(1+\frac \, x \right)^ \end for real ''x'' > 0. Here \mathrm is the beta function. In many applications, the parameters ''d''1 and ''d''2 are positive integers, but the distribution is well-d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |