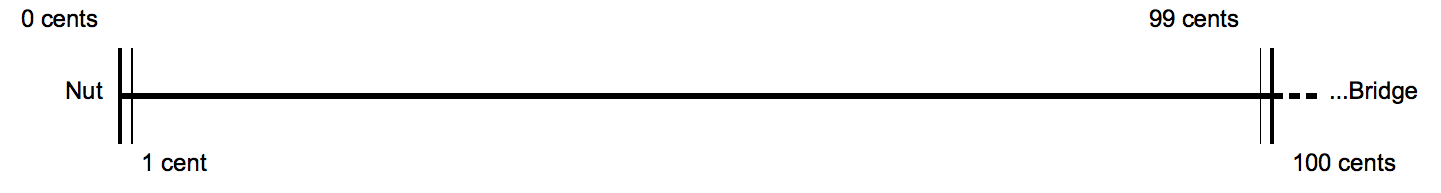|
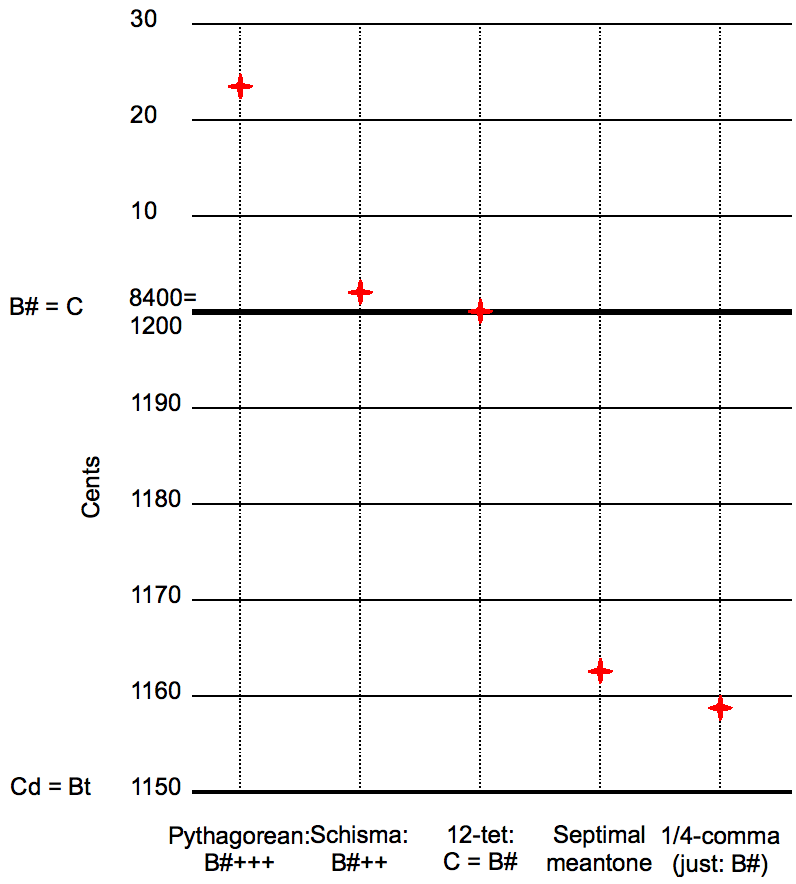
Meantone Temperament
Meantone temperaments are musical temperaments; that is, a variety of Musical tuning#Tuning systems, tuning systems constructed, similarly to Pythagorean tuning, as a sequence of equal fifths, both rising and descending, scaled to remain within the same octave. But rather than using perfect fifths, consisting of frequency ratios of value 3:2, these are ''tempered'' by a suitable factor that narrows them to ratios that are slightly less than 3:2, in order to bring the major or minor thirds closer to Just intonation, the just intonation ratio of 5:4 or 6:5 , respectively. Among temperaments constructed as a sequence of fifths, a regular temperament is one in which all the fifths are chosen to be of the same size. Twelve-tone equal temperament () is obtained by making all semitones the same size, with each equal to one-twelfth of an octave; i.e. with ratios . Relative to Pythagorean tuning, it narrows the perfect fifths by about 2 cents (music), cents or of a Pythagorean co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Temperaments
In musical tuning, a temperament is a tuning system that slightly compromises the pure intervals of just intonation to meet other requirements. Most modern Western musical instruments are tuned in the equal temperament system. Tempering is the process of altering the size of an interval by making it narrower or wider than pure. "Any plan that describes the adjustments to the sizes of some or all of the twelve perfect fifth, fifth intervals in the circle of fifths so that they accommodate pure octaves and produce certain sizes of major thirds is called a ''temperament''." Temperament is especially important for keyboard instruments, which typically allow a player to play only the pitches assigned to the various key (music), keys, and lack any way to alter pitch of a note in performance. Historically, the use of just intonation, Pythagorean tuning and meantone temperament meant that such instruments could sound "in tune" in one key, or some keys, but would then have more dissonance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Third-comma Meantone
In music, 19 equal temperament, called 19 TET, 19 EDO ("Equal Division of the Octave"), 19-ED2 ("Equal Division of 2:1) or 19 Equal temperament, ET, is the musical temperament, tempered scale derived by dividing the octave into 19 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 63.16 cent (music), cents (). The fact that traditional western music maps unambiguously onto this scale (unless it presupposes 12-EDO enharmonic equivalences) makes it easier to perform such music in this tuning than in many other tunings. 19 EDO is the tuning of the syntonic temperament in which the tempered perfect fifth is equal to 694.737 cents, as shown in Figure 1 (look for the label "19 TET"). On an isomorphic keyboard, the fingering of music composed in 19 EDO is precisely the same as it is in any other syntonic tuning (such as 12-TET, 12 EDO), so long as the notes are "spelled properly" – that is, with no assumption t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Music Theory
Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory": The first is the "Elements of music, rudiments", that are needed to understand Musical notation, music notation (key signatures, time signatures, and Chord chart, rhythmic notation); the second is learning scholars' views on music from Ancient history, antiquity to the present; the third is a sub-topic of musicology that "seeks to define processes and general principles in music". The musicological approach to theory differs from music analysis "in that it takes as its starting-point not the individual work or performance but the fundamental materials from which it is built." Music theory is frequently concerned with describing how musicians and composers make music, including Musical tuning, tuning systems and composition methods among other topics. Because of the ever-expan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marin Mersenne
Marin Mersenne, OM (also known as Marinus Mersennus or ''le Père'' Mersenne; ; 8 September 1588 – 1 September 1648) was a French polymath whose works touched a wide variety of fields. He is perhaps best known today among mathematicians for Mersenne prime numbers, those written in the form for some integer . He also developed Mersenne's laws, which describe the harmonics of a vibrating string (such as may be found on guitars and pianos), and his seminal work on music theory, '' Harmonie universelle'', for which he is referred to as the "father of acoustics". Mersenne, an ordained Catholic priest, had many contacts in the scientific world and has been called "the center of the world of science and mathematics during the first half of the 1600s" and, because of his ability to make connections between people and ideas, "the post-box of Europe". He was also a member of the ascetical Minim religious order and wrote and lectured on theology and philosophy. Life Mersenne was b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Francisco De Salinas
Francisco de Salinas (1513, Burgos – 1590, Salamanca) was a Spanish music theorist and organist, noted as among the first to describe meantone temperament in mathematically precise terms, and one of the first (along with Guillaume Costeley) to describe, in effect, 19 equal temperament. In his ''De musica libri septem'' of 1577 he discusses 1/3-, 1/4- and 2/7-comma meantone tunings. Of 1/3-comma meantone, which is essentially identical to the meantone of 19-et, he remarks that it is "languid" but not "offensive to the ear", and he notes that a keyboard of 19 tones to the octave suffices to give a circulating version of meantone. The 19th-century musicologist Alexander John Ellis maintained that Salinas really meant to characterize 1/6-comma meantone, and made a mistake due to his blindness. Others point out that Salinas's descriptions of his tuning as "languid" but not "offensive to the ear" seem to apply to 1/3-comma meantone, not to 1/6-comma meantone, which in any case has a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gioseffo Zarlino
Gioseffo Zarlino (31 January or 22 March 1517 – 4 February 1590) was an Italian Music theory, music theorist and composer of the Renaissance music, Renaissance. He made a large contribution to the theory of counterpoint as well as to musical tuning. Life and career Zarlino was born in Chioggia, near Venice. His early education was with the Franciscans, and he later joined the order himself. In 1536 he was a singer at Chioggia Cathedral, and by 1539 he not only became a deacon, but also principal organist. In 1540 he was ordained, and in 1541 went to Venice to study with the famous contrapuntist and ''maestro di cappella'' of San Marco di Venezia, Saint Mark's, Adrian Willaert. In 1565, on the resignation of Cipriano de Rore, Zarlino took over the post of ''maestro di cappella'' of St. Mark's, one of the most prestigious musical positions in Italy, and held it until his death. While ''maestro di cappella'' he taught some of the principal figures of the Venetian School (musi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pietro Aron
Pietro Aron, also known as Pietro (or Piero) Aaron (c. 1480 – after 1545), was an Italian music theorist and composer. He was born in Florence and probably died in Bergamo (other sources state Florence or Venice). Biography Very little is known about Aron's early life but at least one source claims he may have been Jewish. He was educated in Italy. Aron was a self-taught musician. He claimed in his ''Toscanello in musica'' (1523) that he had been friends with Obrecht, Josquin, and Heinrich Isaac in Florence. If true, the time frame would have been most likely in 1487. Between 1515 and 1522, he was Church Cantor at the Cathedral of Imola. In 1516 he became a priest there. In February 1523 Aron went to Venice and became cantor of Rimini Cathedral, where he worked for Sebastiano Michiel, who was Grand Prior of the Knights of St. John of Jerusalem. In 1525, he was "maestro di casa" in a Venetian house. In 1536, after the death of Michiel, he joined a monastery in Bergamo whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Franchinus Gaffurius
Franchinus Gaffurius (Franchino Gaffurio; 14 January 1451 – 25 June 1522) was an Italian music theorist and composer of the Renaissance. Life He was born in Lodi to an aristocratic family. Early in life he entered a Benedictine monastery, where he acquired his early musical training; later he became a priest. Later he lived in Mantua and Verona before settling in Milan as the ''maestro di cappella'' at the cathedral there, a position which he accepted in January 1484. During the previous decade the Sforza family, using the composer Gaspar van Weerbeke as a recruiter, had built the choir at their chapel in Milan into one of the largest and most distinguished musical ensembles in Europe: composer-singers such as Alexander Agricola, Loyset Compère and Johannes Martini had all been employed there. While the membership of the choir at the Milan cathedral was mostly Italian, the cross-influence between his choir and the group at the Sforza chapel was significant. Gaffu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Cents
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, to check intonation, or to compare the sizes of comparable intervals in different tuning systems. For humans, a single cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, \sqrt 200/math>, at Robert Holford Macdowell Bosanquet's suggestion. Making extensive measurements of musical instruments from around the world, Ellis used cents to report and compare the scales employed, and further described and utilized the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Cent
The cent is a logarithmic scale, logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, to Electronic tuner, check intonation, or to compare the sizes of comparable intervals in different tuning systems. For humans, a single cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, \sqrt[1200], at Robert Holford Macdowell Bosanquet's suggestion. Making extensive measurements of musical instruments from around the world, Ellis used cents to report and compare the scales employed, and further described and utilized the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite collection of positive real numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean of numbers is the Nth root, th root of their product (mathematics), product, i.e., for a collection of numbers , the geometric mean is defined as : \sqrt[n]. When the collection of numbers and their geometric mean are plotted in logarithmic scale, the geometric mean is transformed into an arithmetic mean, so the geometric mean can equivalently be calculated by taking the natural logarithm of each number, finding the arithmetic mean of the logarithms, and then returning the result to linear scale using the exponential function , :\sqrt[n] = \exp \left( \frac \right). The geometric mean of two numbers is the square root of their product, for example with numbers and the geometric mean is \textstyle \sqrt = The geometric mean o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |