|
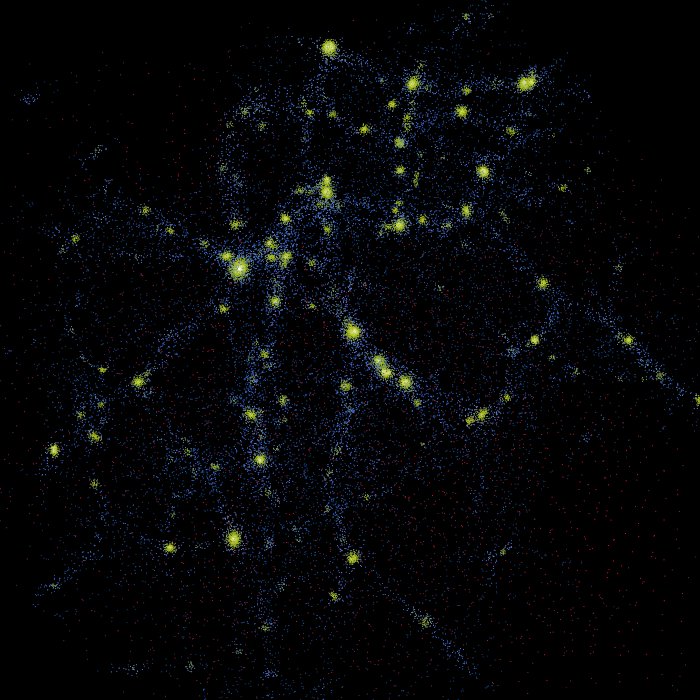
Matter Power Spectrum
The matter power spectrum describes the density contrast of the universe (the difference between the local density and the mean density) as a function of scale. It is the Fourier transform of the matter correlation function. On large scales, gravity competes with cosmic expansion, and structures grow according to linear theory. In this regime, the density contrast field is Gaussian, Fourier modes evolve independently, and the power spectrum is sufficient to completely describe the density field. On small scales, gravitational collapse is non-linear, and can only be computed accurately using N-body simulations. Higher-order statistics are necessary to describe the full field at small scales. Definition Let \delta(\mathbf x) represent the matter overdensity, a dimensionless quantity defined as: \delta(\mathbf x) = \frac, where \bar\rho is the average matter density over all space. The power spectrum is most commonly understood as the Fourier transform of the autocorrela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planck 2018 Linear Matter Power Spectrum
Max Karl Ernst Ludwig Planck (; ; 23 April 1858 – 4 October 1947) was a German Theoretical physics, theoretical physicist whose discovery of energy quantum, quanta won him the Nobel Prize in Physics in 1918. Planck made many substantial contributions to theoretical physics, but his fame as a physicist rests primarily on his role as the originator of Quantum mechanics, quantum theory and one of the founders of modern physics, which revolutionized understanding of atomic and Subatomic particle, subatomic processes. He is known for the Planck constant, which is of foundational importance for quantum physics, and which he used to derive a set of Unit of measurement, units, today called Planck units, expressed only in terms of fundamental physical constants. Planck was twice president of the German scientific institution Kaiser Wilhelm Society. In 1948, it was renamed the Max Planck Society (Max-Planck-Gesellschaft) and nowadays includes 83 institutions representing a wide range ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Spectrum
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of Power (physics), power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of any sort of signal (including Noise (electronics), noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (PSD, or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The PSD then refers to the spectr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Function (astronomy)
In astronomy, a correlation function describes the distribution of objects (often stars or galaxies) in the universe. By default, "correlation function" refers to the two-point autocorrelation function. The two-point autocorrelation function is a function of one variable (distance); it describes the excess probability of finding two galaxies separated by this distance (excess over and above the probability that would arise if the galaxies were simply scattered independently and with uniform probability). It can be thought of as a "clumpiness" factor - the higher the value for some distance scale, the more "clumpy" the universe is at that distance scale. The following definition (from Peebles 1980) is often cited: : ''Given a random galaxy in a location, the correlation function describes the probability that another galaxy will be found within a given distance.'' However, it can only be correct in the statistical sense that it is averaged over a large number of galaxies cho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force between objects and the Earth. This force is dominated by the combined gravitational interactions of particles but also includes effect of the Earth's rotation. Gravity gives weight to physical objects and is essential to understanding the mechanisms responsible for surface water waves and lunar tides. Gravity also has many important biological functions, helping to guide the growth of plants through the process of gravitropism and influencing the circulation of fluids in multicellular organisms. The gravitational attraction between primordial hydrogen and clumps of dark matter in the early universe caused the hydrogen gas to coalesce, eventually condensing and fusing to form stars. At larger scales this results in galaxies and clust ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosmic Expansion
The expansion of the universe is the increase in distance between gravitationally unbound parts of the observable universe with time. It is an intrinsic expansion, so it does not mean that the universe expands "into" anything or that space exists "outside" it. To any observer in the universe, it appears that all but the nearest galaxies (which are bound to each other by gravity) move away at speeds that are proportional to their distance from the observer, on average. While objects cannot move faster than light, this limitation applies only with respect to local reference frames and does not limit the recession rates of cosmologically distant objects. Cosmic expansion is a key feature of Big Bang cosmology. It can be modeled mathematically with the Friedmann–Lemaître–Robertson–Walker metric (FLRW), where it corresponds to an increase in the scale of the spatial part of the universe's spacetime metric tensor (which governs the size and geometry of spacetime). Within thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structure Formation
In physical cosmology, structure formation describes the creation of galaxies, galaxy clusters, and larger structures starting from small fluctuations in mass density resulting from processes that created matter. The universe, as is now known from observations of the cosmic microwave background radiation, began in a hot, dense, nearly uniform state approximately 13.8 billion years ago. However, looking at the night sky today, structures on all scales can be seen, from stars and planets to galaxies. On even larger scales, galaxy clusters and sheet-like structures of galaxies are separated by enormous voids containing few galaxies. Structure formation models gravitational instability of small ripples in mass density to predict these shapes, confirming the consistency of the physical model. The modern Lambda-CDM model is successful at predicting the observed large-scale distribution of galaxies, clusters and voids; but on the scale of individual galaxies there are many complicatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-body Simulation
In physics and astronomy, an ''N''-body simulation is a simulation of a dynamical system of particles, usually under the influence of physical forces, such as gravity (see n-body problem, ''n''-body problem for other applications). ''N''-body simulations are widely used tools in astrophysics, from investigating the dynamics of few-body systems like the Earth-Moon-Sun system to understanding the evolution of the large-scale structure of the universe. In physical cosmology, ''N''-body simulations are used to study processes of non-linear structure formation such as galaxy filaments and galaxy halos from the influence of dark matter. Direct ''N''-body simulations are used to study the dynamical evolution of star clusters. Nature of the particles The 'particles' treated by the simulation may or may not correspond to physical objects which are particulate in nature. For example, an N-body simulation of a star cluster might have a particle per star, so each particle has some physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-point Correlation Function
In astronomy, a correlation function describes the distribution of objects (often stars or galaxies) in the universe. By default, "correlation function" refers to the two-point autocorrelation function. The two-point autocorrelation function is a function of one variable (distance); it describes the excess probability of finding two galaxies separated by this distance (excess over and above the probability that would arise if the galaxies were simply scattered independently and with uniform probability). It can be thought of as a "clumpiness" factor - the higher the value for some distance scale, the more "clumpy" the universe is at that distance scale. The following definition (from Peebles 1980) is often cited: : ''Given a random galaxy in a location, the correlation function describes the probability that another galaxy will be found within a given distance.'' However, it can only be correct in the statistical sense that it is averaged over a large number of galaxies cho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be Heuristic, represented heuristically as \delta (x) = \begin 0, & x \neq 0 \\ , & x = 0 \end such that \int_^ \delta(x) dx=1. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limit (mathematics), limits or, as is common in mathematics, measure theory and the theory of distribution (mathematics), distributions. The delta function was introduced by physicist Paul Dirac, and has since been applied routinely in physics and engineering to model point masses and instantaneous impulses. It is called the delta function because it is a continuous analogue of the Kronecker delta function, which is usually defined on a discrete domain and takes values ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edward Robert Harrison
Edward R. Harrison (8 January 1919 – 29 January 2007) "Physics Today Obituaries: Edward R. (Ted) Harrison", William M. Irvine, PhysicsToday.org, 2007-02-23, webpage: PToday-125 was a British astronomer and cosmologist, noted for his work about the increase of fluctuations in the expanding universe, for his explanation of Olbers's paradox, and for his books on cosmology for lay readers.Astronomy Online , 2004-2007. , MSN Encarta, 2007. 2009-10-31.) He spent much of his career at the |
Yakov Zeldovich
Yakov Borisovich Zeldovich (, ; 8 March 1914 – 2 December 1987), also known as YaB, was a leading Soviet people, Soviet Physics, physicist of Belarusians, Belarusian origin, who is known for his prolific contributions in physical Physical cosmology, cosmology, physics of Plasma physics, thermonuclear reactions, combustion, and Fluid dynamics, hydrodynamical phenomena. From 1943, Zeldovich, a self-taught physicist, started his career by playing a crucial role in the development of the former Soviet atomic bomb project, Soviet program of nuclear weapons. In 1963, he returned to academia to embark on pioneering contributions on the fundamental understanding of the Black hole thermodynamics, thermodynamics of black holes and expanding the scope of physical cosmology. Biography Early life and education Yakov Zeldovich was born into a History of the Jews in Belarus, Belarusian Jewish family in his grandfather's house in Minsk. However, in mid-1914, the Zeldovich family moved to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |