|
Marginal Model
In statistics, marginal models (Heagerty & Zeger, 2000) are a technique for obtaining regression estimates in multilevel modeling, also called hierarchical linear models. People often want to know the effect of a predictor/explanatory variable ''X'', on a response variable ''Y''. One way to get an estimate for such effects is through regression analysis. Why the name marginal model? In a typical multilevel model, there are level 1 & 2 residuals (R and U variables). The two variables form a joint distribution for the response variable (Y_). In a marginal model, we collapse over the level 1 & 2 residuals and thus ''marginalize'' (see also conditional probability) the joint distribution into a univariate normal distribution In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu .... We then fit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multilevel Model
Multilevel models (also known as hierarchical linear models, linear mixed-effect model, mixed models, nested data models, random coefficient, random-effects models, random parameter models, or split-plot designs) are statistical models of parameters that vary at more than one level. An example could be a model of student performance that contains measures for individual students as well as measures for classrooms within which the students are grouped. These models can be seen as generalizations of linear models (in particular, linear regression), although they can also extend to non-linear models. These models became much more popular after sufficient computing power and software became available. Multilevel models are particularly appropriate for research designs where data for participants are organized at more than one level (i.e., nested data). The units of analysis are usually individuals (at a lower level) who are nested within contextual/aggregate units (at a higher level ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
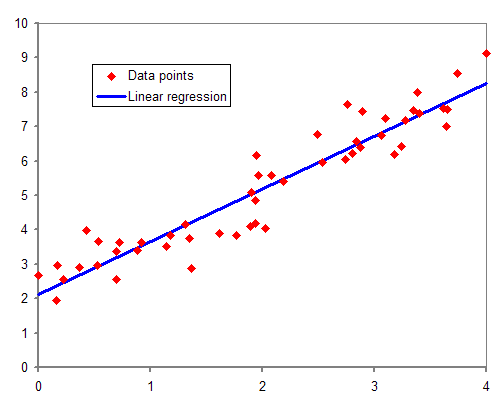
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joint Distribution
Given two random variables that are defined on the same probability space, the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered for any given number of random variables. The joint distribution encodes the marginal distributions, i.e. the distributions of each of the individual random variables. It also encodes the conditional probability distributions, which deal with how the outputs of one random variable are distributed when given information on the outputs of the other random variable(s). In the formal mathematical setup of measure theory, the joint distribution is given by the pushforward measure, by the map obtained by pairing together the given random variables, of the sample space's probability measure. In the case of real-valued random variables, the joint distribution, as a particular multivariate distribution, may be expressed by a multivariate cumulat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. This particular method relies on event B occurring with some sort of relationship with another event A. In this event, the event B can be analyzed by a conditional probability with respect to A. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A: P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day may be only 5%. But if we know or assume that the person is sick, then they are much more likely to be coughing. For example, the conditional probability that someone unwell (sick) is coughing might b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |