|
Literal Movement Grammar
In linguistics and theoretical computer science, literal movement grammars (LMGs) are a grammar formalism intended to characterize certain extraposition phenomena of natural language such as topicalization and cross-serial dependency. LMGs extend the class of context free grammars (CFGs) by adding introducing pattern-matched function-like rewrite semantics, as well as the operations of variable binding and slash deletion. LMGs were introduced by A.V. Groenink in 1995.Groenink, Annius V. 1995. Literal Movement Grammars. In ''Proceedings of the 7th EACL Conference''. Description The basic rewrite operation of an LMG is very similar to that of a CFG, with the addition of arguments to the non-terminal symbols. Where a context-free rewrite rule obeys the general schema S \to \alpha for some non-terminal S and some string of terminals and/or non-terminals \alpha, an LMG rewrite rule obeys the general schema X(x_1, ..., x_n) \to \alpha, where X is a non-terminal with arity n (called a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linguistics
Linguistics is the scientific study of language. The areas of linguistic analysis are syntax (rules governing the structure of sentences), semantics (meaning), Morphology (linguistics), morphology (structure of words), phonetics (speech sounds and equivalent gestures in sign languages), phonology (the abstract sound system of a particular language, and analogous systems of sign languages), and pragmatics (how the context of use contributes to meaning). Subdisciplines such as biolinguistics (the study of the biological variables and evolution of language) and psycholinguistics (the study of psychological factors in human language) bridge many of these divisions. Linguistics encompasses Outline of linguistics, many branches and subfields that span both theoretical and practical applications. Theoretical linguistics is concerned with understanding the universal grammar, universal and Philosophy of language#Nature of language, fundamental nature of language and developing a general ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Argument (linguistics)
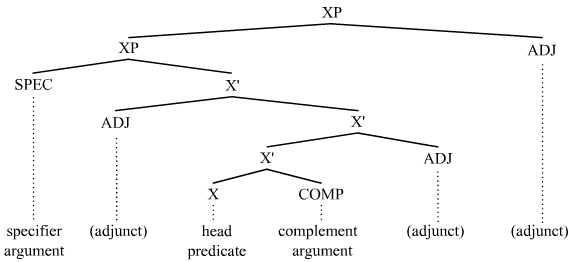
In linguistics, an argument is an expression that helps complete the meaning of a predicate (grammar), predicate, the latter referring in this context to a main verb and its auxiliaries. In this regard, the ''Complement (linguistics), complement'' is a closely related concept. Most predicates take one, two, or three arguments. A predicate and its arguments form a ''predicate-argument structure''. The discussion of predicates and arguments is associated most with (content) verbs and noun phrases (NPs), although other syntactic category, syntactic categories can also be construed as predicates and as arguments. Arguments must be distinguished from adjunct (grammar), adjuncts. While a predicate needs its arguments to complete its meaning, the adjuncts that appear with a predicate are optional; they are not necessary to complete the meaning of the predicate. Most theories of syntax and semantics acknowledge arguments and adjuncts, although the terminology varies, and the distinction is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Production (computer Science)
In computer science, a production or production rule is a rewrite rule that replaces some symbols with other symbols. A finite set of productions P is the main component in the specification of a formal grammar (specifically a generative grammar). The other components are a finite set N of nonterminal symbols, a finite set (known as an alphabet) \Sigma of terminal symbols that is disjoint from N and a distinguished symbol S \in N that is the ''start symbol''. In an unrestricted grammar, a production is of the form u \to v, where u and v are arbitrary strings of terminals and nonterminals, and u may not be the empty string. If v is the empty string, this is denoted by the symbol \epsilon, or \lambda (rather than leaving the right-hand side blank). So productions are members of the cartesian product :V^*NV^* \times V^* = (V^*\setminus\Sigma^*) \times V^*, where V := N \cup \Sigma is the ''vocabulary'', ^ is the Kleene star operator, V^*NV^* indicates concatenation, \cup deno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. When quantified, A \subseteq B is represented as \forall x \left(x \in A \Rightarrow x \in B\right). One can prove the statement A \subseteq B by applying a proof technique known as the element argument:Let sets ''A'' and ''B'' be given. To prove that A \subseteq B, # suppose that ''a'' is a particular but arbitrarily chosen element of A # show that ''a'' is an element of ''B''. The validity of this technique ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predicate (grammar)
The term predicate is used in two ways in linguistics and its subfields. The first defines a predicate as everything in a standard declarative sentence except the subject (grammar), subject, and the other defines it as only the main content verb or associated predicative expression of a clause. Thus, by the first definition, the predicate of the sentence ''Frank likes cake'' is ''likes cake'', while by the second definition, it is only the content verb ''likes'', and ''Frank'' and ''cake'' are the argument (linguistics), arguments of this predicate. The conflict between these two definitions can lead to confusion. Syntax Traditional grammar The notion of a predicate in traditional grammar traces back to Aristotelian logic. A predicate is seen as a property that a subject has or is characterized by. A predicate is therefore an expression that can be ''true of'' something. Thus, the expression "is moving" is true of anything that is moving. This classical understanding of pred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arity
In logic, mathematics, and computer science, arity () is the number of arguments or operands taken by a function, operation or relation. In mathematics, arity may also be called rank, but this word can have many other meanings. In logic and philosophy, arity may also be called adicity and degree. In linguistics, it is usually named valency. Examples In general, functions or operators with a given arity follow the naming conventions of ''n''-based numeral systems, such as binary and hexadecimal. A Latin prefix is combined with the -ary suffix. For example: * A nullary function takes no arguments. ** Example: f()=2 * A unary function takes one argument. ** Example: f(x)=2x * A binary function takes two arguments. ** Example: f(x,y)=2xy * A ternary function takes three arguments. ** Example: f(x,y,z)=2xyz * An ''n''-ary function takes ''n'' arguments. ** Example: f(x_1, x_2, \ldots, x_n)=2\prod_^n x_i Nullary A constant can be treated as the output of an operation o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String (computer Science)
In computer programming, a string is traditionally a sequence of character (computing), characters, either as a literal (computer programming), literal constant or as some kind of Variable (computer science), variable. The latter may allow its elements to be Immutable object, mutated and the length changed, or it may be fixed (after creation). A string is often implemented as an array data structure of bytes (or word (computer architecture), words) that stores a sequence of elements, typically characters, using some character encoding. More general, ''string'' may also denote a sequence (or List (abstract data type), list) of data other than just characters. Depending on the programming language and precise data type used, a variable (programming), variable declared to be a string may either cause storage in memory to be statically allocated for a predetermined maximum length or employ dynamic allocation to allow it to hold a variable number of elements. When a string appears lit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schema (logic)
In logic, the logical form of a statement is a precisely specified semantic version of that statement in a formal system. Informally, the logical form attempts to formalize a possibly ambiguous statement into a statement with a precise, unambiguous logical interpretation with respect to a formal system. In an ideal formal language, the meaning of a logical form can be determined unambiguously from syntax alone. Logical forms are semantic, not syntactic constructs; therefore, there may be more than one string that represents the same logical form in a given language. The logical form of an argument is called the argument form of the argument. History The importance of the concept of form to logic was already recognized in ancient times. Aristotle, in the '' Prior Analytics'', was one of the first people to employ variable letters to represent valid inferences. Therefore, Jan Łukasiewicz claims that the introduction of variables was "one of Aristotle's greatest inventions." ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines, or reduction systems). In their most basic form, they consist of a set of objects, plus relations on how to transform those objects. Rewriting can be non-deterministic. One rule to rewrite a term could be applied in many different ways to that term, or more than one rule could be applicable. Rewriting systems then do not provide an algorithm for changing one term to another, but a set of possible rule applications. When combined with an appropriate algorithm, however, rewrite systems can be viewed as computer programs, and several theorem provers and declarative programming languages are based on term rewriting. Example cases Logic In logic, the procedure for obtaining the conjunctive normal form (CNF) of a formula can be implemented as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Computer Science
Theoretical computer science is a subfield of computer science and mathematics that focuses on the Abstraction, abstract and mathematical foundations of computation. It is difficult to circumscribe the theoretical areas precisely. The Association for Computing Machinery, ACM's Special Interest Group on Algorithms and Computation Theory (SIGACT) provides the following description: History While logical inference and mathematical proof had existed previously, in 1931 Kurt Gödel proved with his incompleteness theorem that there are fundamental limitations on what statements could be proved or disproved. Information theory was added to the field with A Mathematical Theory of Communication, a 1948 mathematical theory of communication by Claude Shannon. In the same decade, Donald Hebb introduced a mathematical model of Hebbian learning, learning in the brain. With mounting biological data supporting this hypothesis with some modification, the fields of neural networks and para ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Variables And Bound Variables
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a variable may be said to be either free or bound. Some older books use the terms real variable and apparent variable for free variable and bound variable, respectively. A ''free variable'' is a Mathematical notation, notation (symbol) that specifies places in an expression (mathematics), expression where Substitution (logic), substitution may take place and is not a parameter of this or any container expression. The idea is related to a ''placeholder'' (a symbol that will later be replaced by some value), or a wildcard character that stands for an unspecified symbol. In computer programming, the term free variable refers to variable (programming), variables used in a function (computer science), function that are neither local variables nor parameter (computer programming), parameters of that function. The term non-local variable is often a synonym in this co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Context Free Grammar
In formal language theory, a context-free grammar (CFG) is a formal grammar whose Production (computer science), production rules can be applied to a Terminal and nonterminal symbols, nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form : A\ \to\ \alpha with A a ''single'' nonterminal symbol, and \alpha a string of terminals and/or nonterminals (\alpha can be empty). Regardless of which symbols surround it, the single nonterminal A on the left hand side can always be replaced by \alpha on the right hand side. This distinguishes it from a context-sensitive grammar, which can have production rules in the form \alpha A \beta \rightarrow \alpha \gamma \beta with A a nonterminal symbol and \alpha, \beta, and \gamma strings of terminal and/or nonterminal symbols. A formal grammar is essentially a set of production rules that describe all possible strings in a given formal language. Production rules are simple rep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |