|
List Of Common Physics Notations
This is a list of common physical constants and variables, and their notations. Note that bold text indicates that the quantity is a vector. Latin characters Greek characters Other characters See also * List of letters used in mathematics and science * Glossary of mathematical symbols * List of mathematical uses of Latin letters * Greek letters used in mathematics, science, and engineering * Physical constant * Physical quantity * International System of Units * ISO 31 ISO 31 (Physical quantity, Quantities and Physical unit, units, International Organization for Standardization, 1992) is a superseded international standard concerning physical quantities, units of measurement, their interrelationships and their pr ... References * * {{DEFAULTSORT:List Of Common Physics Notations Common Physics Abbreviations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector (geometry)
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Euclidean vectors can be added and scaled to form a vector space. A '' vector quantity'' is a vector-valued physical quantity, including units of measurement and possibly a support, formulated as a '' directed line segment''. A vector is frequently depicted graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \stackrel \longrightarrow. A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word means 'carrier'. It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Of Integration
In calculus, the constant of integration, often denoted by C (or c), is a constant term added to an antiderivative of a function f(x) to indicate that the indefinite integral of f(x) (i.e., the set of all antiderivatives of f(x)), on a connected domain, is only defined up to an additive constant. This constant expresses an ambiguity inherent in the construction of antiderivatives. More specifically, if a function f(x) is defined on an interval, and F(x) is an antiderivative of f(x), then the set of ''all'' antiderivatives of f(x) is given by the functions F(x) + C, where C is an arbitrary constant (meaning that ''any'' value of C would make F(x) + C a valid antiderivative). For that reason, the indefinite integral is often written as \int f(x) \, dx = F(x) + C, although the constant of integration might be sometimes omitted in lists of integrals for simplicity. Origin The derivative of any constant function is zero. Once one has found one antiderivative F(x) for a function f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Direction
In geometry, direction, also known as spatial direction or vector direction, is the common characteristic of all ray (geometry), rays which coincide when translation (geometry), translated to share a common endpoint; equivalently, it is the common characteristic of vector (geometry), vectors (such as the relative position between a pair of points) which can be made equal by scaling (geometry), scaling (by some positive scalar multiplication, scalar multiplier). Two vectors sharing the same direction are said to be ''codirectional'' or ''equidirectional''. All codirectional line segments sharing the same size (length) are said to be ''equipollent (geometry), equipollent''. Two equipollent segments are not necessarily coincident; for example, a given direction can be evaluated at different starting Position (geometry), positions, defining different unit directed line segments (as a bound vector instead of a free vector). A direction is often represented as a unit vector, the res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two counties over"). The term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects (such as statistical distance between probability distributions or edit distance between string (computer science), strings of text) or a degree of separation (as exemplified by distance (graph theory), distance between people in a social network). Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space. In the social sciences, distance can refer to a qualitative measurement of separation, such as social distance or psychological distance. Distances in physics and geometry The distance between physical locations can be defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. The word "diameter" is derived from (), "diameter of a circle", from (), "across, through" and (), "measure". It is often abbreviated \text, \text, d, or \varnothing. Constructions With straightedge and compass, a diameter of a given circle can be constructed as the perpendicular bisector of an arbitrary chord. Drawing two diameters in this way can be used to locate the center of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Meter
The cubic metre (in Commonwealth English and international spelling as used by the International Bureau of Weights and Measures) or cubic meter (in American English) is the unit of volume in the International System of Units (SI). Its symbol is m3. Bureau International de Poids et Mesures.Derived units expressed in terms of base units". 2014. Accessed 7 August 2014. It is the volume of a cube with edges one metre in length. An alternative name, which allowed a different usage with metric prefixes, was the stère, still sometimes used for dry measure (for instance, in reference to wood). Another alternative name, no longer widely used, was the kilolitre. Conversions : A cubic metre of pure water at the temperature of maximum density (3.983 °C) and standard atmospheric pressure (101.325 kPa) has a mass of , or one tonne. At 0 °C, the freezing point of water, a cubic metre of water has slightly less mass, 999.85 kilograms. A cubic metre is sometimes abbreviated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be used: \rho = \frac, where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate this quantity is more specifically called specific weight. For a pure substance, the density is equal to its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium is the densest known element at standard conditions for temperature and pressure. To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative den ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coulomb
The coulomb (symbol: C) is the unit of electric charge in the International System of Units (SI). It is defined to be equal to the electric charge delivered by a 1 ampere current in 1 second, with the elementary charge ''e'' as a defining constant in the SI. Definition The SI defines the coulomb as "the quantity of electricity carried in 1 second by a current of 1 ampere" by fixing the value of the elementary charge, . Inverting the relationship, the coulomb can be expressed in terms of the elementary charge: 1 ~ \mathrm = \frac = \frac ~ e. It is approximately and is thus not an integer multiple of the elementary charge. The coulomb was previously defined in terms of the ampere based on the force between two wires, as . The 2019 redefinition of the ampere and other SI base units fixed the numerical value of the elementary charge when expressed in coulombs and therefore fixed the value of the coulomb when expressed as a multiple of the fundamental charge. SI pref ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Displacement Field
In physics, the electric displacement field (denoted by D), also called electric flux density, is a vector field that appears in Maxwell's equations. It accounts for the electromagnetic effects of polarization and that of an electric field, combining the two in an auxiliary field. It plays a major role in the physics of phenomena such as the capacitance of a material, the response of dielectrics to an electric field, how shapes can change due to electric fields in piezoelectricity or flexoelectricity as well as the creation of voltages and charge transfer due to elastic strains. In any material, if there is an inversion center then the charge at, for instance, +x and -x are the same. This means that there is no dipole. If an electric field is applied to an insulator, then (for instance) the negative charges can move slightly towards the positive side of the field, and the positive charges in the other direction. This leads to an induced dipole which is described as a pola ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
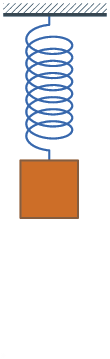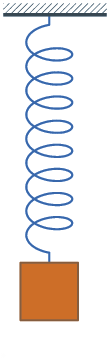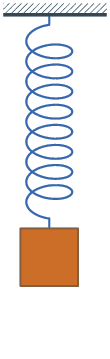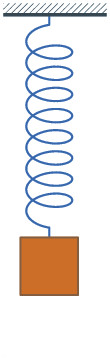
Damping
In physical systems, damping is the loss of energy of an oscillating system by dissipation. Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. Examples of damping include viscous damping in a fluid (see viscous drag), surface friction, radiation, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes (ex. Suspension (mechanics)). Damping is not to be confused with friction, which is a type of dissipative force acting on a system. Friction can cause or be a factor of damping. Many systems exhibit oscillatory behavior when they are disturbed from their position of static equilibrium. A mass suspended from a spring, for example, might, if pulled and released, bounce up and down. On each bounce, the system tends to return to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kilogram
The kilogram (also spelled kilogramme) is the base unit of mass in the International System of Units (SI), equal to one thousand grams. It has the unit symbol kg. The word "kilogram" is formed from the combination of the metric prefix kilo- (meaning one thousand) and gram; it is colloquially shortened to "kilo" (plural "kilos"). The kilogram is an SI base unit, defined ultimately in terms of three defining constants of the SI, namely a specific transition frequency of the caesium-133 atom, the speed of light, and the Planck constant. A properly equipped metrology laboratory can calibrate a mass measurement instrument such as a Kibble balance as a primary standard for the kilogram mass. The kilogram was originally defined in 1795 during the French Revolution as the mass of one litre of water (originally at 0 °C, later changed to the temperature of its maximum density, approximately 4 °C). The current definition of a kilogram agrees with this original defini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Heat Capacity
In thermodynamics, the specific heat capacity (symbol ) of a substance is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. It is also referred to as massic heat capacity or as the specific heat. More formally it is the heat capacity of a sample of the substance divided by the mass of the sample. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1. For example, the heat required to raise the temperature of of water by is , so the specific heat capacity of water is . Specific heat capacity often varies with temperature, and is different for each state of matter. Liquid water has one of the highest specific heat capacities among common substances, about at 20 °C; but that of ice, just below 0 °C, is only . The specific heat capacities of iron, granite, and hydrogen gas are about 449 J⋅kg−1⋅K−1, 790 J⋅kg−1⋅K−1, and 143 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |