|
List Of Mathematical Examples
{{Short description, none This page will attempt to list examples in mathematics. To qualify for inclusion, an article should be about a mathematical object with a fair amount of concreteness. Usually a definition of an abstract concept, a theorem, or a proof would not be an "example" as the term should be understood here (an elegant proof of an isolated but particularly striking fact, as opposed to a proof of a general theorem, could perhaps be considered an "example"). The discussion page for list of mathematical topics has some comments on this. Eventually this page may have its own discussion page. This page links to itself in order that edits to this page will be included among related changes when the user clicks on that button. The concrete example within the article titled Rao-Blackwell theorem is perhaps one of the best ways for a List of mathematical probabilists, probabilist ignorant of statistical inference to get a quick impression of the flavor of that subject. Un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Mathematical Topics
Mathematics is a field of study that investigates topics such as number, space, Mathematical structure, structure, and change. Philosophy Nature * Definitions of mathematics – Mathematics has no generally accepted definition. Different schools of thought, particularly in philosophy, have put forth radically different definitions, all of which are controversial. * Language of mathematics is the system used by mathematicians to communicate Mathematics, mathematical ideas among themselves, and is distinct from natural languages in that it aims to communicate abstract, logical ideas with precision and unambiguity. * Philosophy of mathematics – its aim is to provide an account of the nature and methodology of mathematics and to understand the place of mathematics in people's lives. :* Classical mathematics refers generally to the mainstream approach to mathematics, which is based on classical logic and ZFC set theory. :* Constructivism (philosophy of mathematics), Constructive mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Examples Of Groups
Some elementary examples of groups in mathematics are given on Group (mathematics). Further examples are listed here. Permutations of a set of three elements Consider three colored blocks (red, green, and blue), initially placed in the order RGB. Let ''a'' be the operation "swap the first block and the second block", and ''b'' be the operation "swap the second block and the third block". We can write ''xy'' for the operation "first do ''y'', then do ''x''"; so that ''ab'' is the operation RGB → RBG → BRG, which could be described as "move the first two blocks one position to the right and put the third block into the first position". If we write ''e'' for "leave the blocks as they are" (the identity operation), then we can write the six permutations of the three blocks as follows: * ''e'' : RGB → RGB * ''a'' : RGB → GRB * ''b'' : RGB → RBG * ''ab'' : RGB → BRG * ''ba'' : RGB → GBR * ''aba'' : RGB → BGR Note that ''aa'' has the effect RGB → GRB → RGB; so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leech Lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space, which is one of the best models for the kissing number problem. It was discovered by . It may also have been discovered (but not published) by Ernst Witt in 1940. Characterization The Leech lattice Λ24 is the unique lattice in 24-dimensional Euclidean space, E24, with the following list of properties: *It is unimodular; i.e., it can be generated by the columns of a certain 24×24 matrix with determinant 1. *It is even; i.e., the square of the length of each vector in Λ24 is an even integer. *The length of every non-zero vector in Λ24 is at least 2. The last condition is equivalent to the condition that unit balls centered at the points of Λ24 do not overlap. Each is tangent to 196,560 neighbors, and this is known to be the largest number of non-overlapping 24-dimensional unit balls that can simultaneously touch a single unit ball. This arrangement of 196,560 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
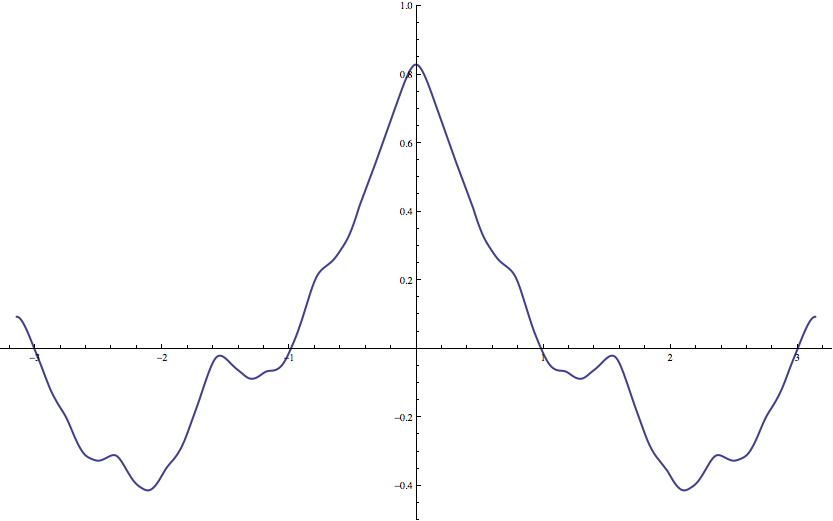
An Infinitely Differentiable Function That Is Not Analytic
In mathematics, smooth functions (also called infinitely differentiable functions) and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth. The converse is not true, as demonstrated with the counterexample below. One of the most important applications of smooth functions with compact support is the construction of so-called mollifiers, which are important in theories of generalized functions, such as Laurent Schwartz's theory of distributions. The existence of smooth but non-analytic functions represents one of the main differences between differential geometry and analytic geometry. In terms of sheaf theory, this difference can be stated as follows: the sheaf of differentiable functions on a differentiable manifold is fine, in contrast with the analytic case. The functions below are generally used to build up partitions of unity on differentiable manifolds. An example function Definition o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Illustration Of The Central Limit Theorem
In probability theory, the central limit theorem (CLT) states that, in many situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution. This article gives two illustrations of this theorem. Both involve the sum of independent and identically-distributed random variables and show how the probability distribution of the sum approaches the normal distribution as the number of terms in the sum increases. The first illustration involves a continuous probability distribution, for which the random variables have a probability density function. The second illustration, for which most of the computation can be done by hand, involves a discrete probability distribution, which is characterized by a probability mass function. Illustration of the continuous case The density of the sum of two independent real-valued random variables equals the convolution of the density functions of the original variables. Thus, the density of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Illustration Of A Low-discrepancy Sequence
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of ''N'', its subsequence ''x''1, ..., ''x''''N'' has a low discrepancy. Roughly speaking, the discrepancy of a sequence is low if the proportion of points in the sequence falling into an arbitrary set ''B'' is close to proportional to the measure of ''B'', as would happen on average (but not for particular samples) in the case of an equidistributed sequence. Specific definitions of discrepancy differ regarding the choice of ''B'' (hyperspheres, hypercubes, etc.) and how the discrepancy for every B is computed (usually normalized) and combined (usually by taking the worst value). Low-discrepancy sequences are also called quasirandom sequences, due to their common use as a replacement of uniformly distributed random numbers. The "quasi" modifier is used to denote more clearly that the values of a low-discrepancy sequence are neither random nor pseudorandom, but such sequences share some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Matrix
In linear algebra, a Hilbert matrix, introduced by , is a square matrix with entries being the unit fractions : H_ = \frac. For example, this is the 5 × 5 Hilbert matrix: : H = \begin 1 & \frac & \frac & \frac & \frac \\ \frac & \frac & \frac & \frac & \frac \\ \frac & \frac & \frac & \frac & \frac \\ \frac & \frac & \frac & \frac & \frac \\ \frac & \frac & \frac & \frac & \frac \end. The Hilbert matrix can be regarded as derived from the integral : H_ = \int_0^1 x^ \, dx, that is, as a Gramian matrix for powers of ''x''. It arises in the least squares approximation of arbitrary functions by polynomials. The Hilbert matrices are canonical examples of ill-conditioned matrices, being notoriously difficult to use in numerical computation. For example, the 2-norm condition number of the matrix above is about 4.8. Historical note introduced the Hilbert matrix to study the following question in approximation theory: "Assume that , is a real interval. Is it then po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Higman–Sims Graph
In mathematical graph theory, the Higman–Sims graph is a 22-regular undirected graph with 100 vertices and 1100 edges. It is the unique strongly regular graph srg(100,22,0,6), where no neighboring pair of vertices share a common neighbor and each non-neighboring pair of vertices share six common neighbors. It was first constructed by and rediscovered in 1968 by Donald G. Higman and Charles C. Sims as a way to define the Higman–Sims group, a subgroup of index two in the group of automorphisms of the Higman–Sims graph. Construction From M22 graph Take the M22 graph, a strongly regular graph srg(77,16,0,4) and augment it with 22 new vertices corresponding to the points of S(3,6,22), each block being connected to its points, and one additional vertex ''C'' connected to the 22 points. From Hoffman–Singleton graph There are 100 independent sets of size 15 in the Hoffman–Singleton graph. Create a new graph with 100 corresponding vertices, and connect vertices whose corre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hall–Janko Graph
In the mathematical field of graph theory, the Hall–Janko graph, also known as the Hall-Janko-Wales graph, is a 36-regular undirected graph with 100 vertices and 1800 edges. It is a rank 3 strongly regular graph with parameters (100,36,14,12) and a maximum coclique of size 10. This parameter set is not unique, it is however uniquely determined by its parameters as a rank 3 graph. The Hall–Janko graph was originally constructed by D. Wales to establish the existence of the Hall-Janko group as an index 2 subgroup of its automorphism group. The Hall–Janko graph can be constructed out of objects in U3(3), the simple group of order 6048: * In U3(3) there are 36 simple maximal subgroups of order 168. These are the vertices of a subgraph, the U3(3) graph. A 168-subgroup has 14 maximal subgroups of order 24, isomorphic to S4. Two 168-subgroups are called adjacent when they intersect in a 24-subgroup. The U3(3) graph is strongly regular, with parameters (36,14,4,6) * There are 63 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gray Graph
Grey (more common in British English) or gray (more common in American English) is an intermediate color between black and white. It is a neutral or achromatic color, meaning literally that it is "without color", because it can be composed of black and white. It is the color of a cloud-covered sky, of ash and of lead. The first recorded use of ''grey'' as a color name in the English language was in 700 CE.Maerz and Paul ''A Dictionary of Color'' New York:1930 McGraw-Hill Page 196 ''Grey'' is the dominant spelling in European and Commonwealth English, while ''gray'' has been the preferred spelling in American English; both spellings are valid in both varieties of English. In Europe and North America, surveys show that grey is the color most commonly associated with neutrality, conformity, boredom, uncertainty, old age, indifference, and modesty. Only one percent of respondents chose it as their favorite color. Etymology ''Grey'' comes from the Middle English or , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frieze Group
In mathematics, a frieze or frieze pattern is a two-dimensional design that repeats in one direction. Such patterns occur frequently in architecture and decorative art. Frieze patterns can be classified into seven types according to their symmetries. The set of symmetry, symmetries of a frieze pattern is called a frieze group. Frieze groups are two-dimensional line groups, having repetition in only one direction. They are related to the more complex wallpaper groups, which classify patterns that are repetitive in two directions, and crystallographic groups, which classify patterns that are repetitive in three directions. General Formally, a frieze group is a class of infinite discrete symmetry groups of patterns on a strip (infinitely wide rectangle), hence a class of groups of isometries of the plane, or of a strip. A symmetry group of a frieze group necessarily contains translations and may contain glide reflections, reflections along the long axis of the strip, reflectio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fano Plane
In finite geometry, the Fano plane (after Gino Fano) is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines cannot exist with this pattern of incidences in Euclidean geometry, but they can be given coordinates using the finite field with two elements. The standard notation for this plane, as a member of a family of projective spaces, is . Here stands for "projective geometry", the first parameter is the geometric dimension (it is a plane, of dimension 2) and the second parameter is the order (the number of points per line, minus one). The Fano plane is an example of a finite incidence structure, so many of its properties can be established using combinatorial techniques and other tools used in the study of incidence geometries. Since it is a projective space, algebraic techniques can also be effective tools in its study. Homogeneous coordi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |