|
List Of Integrable Models
This is a list of integrable models as well as classes of integrable models in physics. Integrable models in 1+1 dimensions In classical and quantum field theory: *free boson *free fermion * sine-Gordon model * Thirring model * sinh-Gordon model *Liouville field theory * Bullough–Dodd model *Dym equation *Calogero–Degasperis–Fokas equation *Camassa–Holm equation * Drinfeld–Sokolov–Wilson equation * Benjamin–Ono equation *SS model *sausage model * Toda field theories *O(''N'')-symmetric non-linear sigma models *Ernst equation * massless Schwinger model *supersymmetric sine-Gordon model *supersymmetric sinh-Gordon model * conformal minimal models *critical Ising model *tricritical Ising model *3-state Potts model *various perturbations of conformal minimal models *superconformal minimal models *Wess–Zumino–Witten model * Nonlinear Schroedinger equation * Korteweg–de Vries equation * modified Korteweg–de Vries equation *Gardner equation * Gibbons–Tsarev equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrable Model
In mathematics, integrability is a property of certain dynamical systems. While there are several distinct formal definitions, informally speaking, an integrable system is a dynamical system with sufficiently many conserved quantities, or first integrals, that its motion is confined to a submanifold of much smaller dimensionality than that of its phase space. Three features are often referred to as characterizing integrable systems: * the existence of a ''maximal'' set of conserved quantities (the usual defining property of complete integrability) * the existence of algebraic invariants, having a basis in algebraic geometry (a property known sometimes as algebraic integrability) * the explicit determination of solutions in an explicit functional form (not an intrinsic property, but something often referred to as solvability) Integrable systems may be seen as very different in qualitative character from more ''generic'' dynamical systems, which are more typically chaotic systems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-dual Yang–Mills Equations
In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures in a one-to-one fashion, often (but not always) by means of an involution operation: if the dual of is , then the dual of is . In other cases the dual of the dual – the double dual or bidual – is not necessarily identical to the original (also called ''primal''). Such involutions sometimes have fixed points, so that the dual of is itself. For example, Desargues' theorem is self-dual in this sense under the ''standard duality in projective geometry''. In mathematical contexts, ''duality'' has numerous meanings. It has been described as "a very pervasive and important concept in (modern) mathematics" and "an important general theme that has manifestations in almost every area of mathematics". Many mathematical dualities between objects of two types correspond to pairings, bilinear functions from an object of one type and another object of the seco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Novikov–Veselov Equation
In mathematics, the Novikov–Veselov equation (or Veselov–Novikov equation) is a natural (2+1)-dimensional analogue of the Korteweg–de Vries (KdV) equation. Unlike another (2+1)-dimensional analogue of KdV, the Kadomtsev–Petviashvili equation, it is integrable via the inverse scattering transform for the 2-dimensional stationary Schrödinger equation. Similarly, the Korteweg–de Vries equation is integrable via the inverse scattering transform for the 1-dimensional Schrödinger equation. The equation is named after S.P. Novikov and A.P. Veselov who published it in . Definition The Novikov–Veselov equation is most commonly written as where v = v( x_1, x_2, t ), w = w( x_1, x_2, t ) and the following standard notation of complex analysis is used: \Re is the real part, : \partial_ = \frac ( \partial_ - i \partial_ ), \quad \partial_ = \frac ( \partial_ + i \partial_ ). The function v is generally considered to be real-valued. The function w is an auxiliary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau–Lifshitz–Gilbert Equation
In physics, the Landau–Lifshitz–Gilbert equation (usually abbreviated as LLG equation), named for Lev Landau, Evgeny Lifshitz, and T. L. Gilbert, is a name used for a differential equation describing the dynamics (typically the precessional motion) of magnetization in a solid. It is a modified version by Gilbert of the original equation of Landau and Lifshitz. The LLG equation is similar to the Bloch equation, but they differ in the form of the damping term. The LLG equation describes a more general scenario of magnetization dynamics beyond the simple Larmor precession. In particular, the effective field driving the precessional motion of is not restricted to real magnetic fields; it incorporates a wide range of mechanisms including magnetic anisotropy, exchange interaction, and so on. The various forms of the LLG equation are commonly used in micromagnetics to model the effects of a magnetic field and other magnetic interactions on ferromagnetic materials. It provides a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kadomtsev–Petviashvili Equation
In mathematics and physics, the Kadomtsev–Petviashvili equation (often abbreviated as KP equation) is a partial differential equation to describe nonlinear wave motion. Named after Boris Kadomtsev, Boris Borisovich Kadomtsev and Vladimir Iosifovich Petviashvili, the KP equation is usually written as \displaystyle \partial_x(\partial_t u+u \partial_x u+\epsilon^2\partial_u)+\lambda\partial_u=0 where \lambda=\pm 1. The above form shows that the KP equation is a generalization to two spatial dimensions, ''x'' and ''y'', of the one-dimensional Korteweg–de Vries equation, Korteweg–de Vries (KdV) equation. To be physically meaningful, the wave propagation direction has to be not-too-far from the ''x'' direction, i.e. with only slow variations of solutions in the ''y'' direction. Like the KdV equation, the KP equation is completely integrable. It can also be solved using the inverse scattering transform much like the nonlinear Schrödinger equation. In 2002, the regularized version ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ishimori Equation
The Ishimori equation is a partial differential equation proposed by the Japanese mathematician . Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable . Equation The Ishimori equation has the form Lax representation The Lax representation of the equation is given by Here the \sigma_i are the Pauli matrices and I is the identity matrix. Reductions The Ishimori equation admits an important reduction: in 1+1 dimensions it reduces to the continuous classical Heisenberg ferromagnet equation (CCHFE). The CCHFE is integrable. Equivalent counterpart The equivalent counterpart of the Ishimori equation is the Davey-Stewartson equation. See also * Nonlinear Schrödinger equation * Heisenberg model (classical) * Spin wave * Landau–Lifshitz model * Soliton * Vortex * Nonlinear systems In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
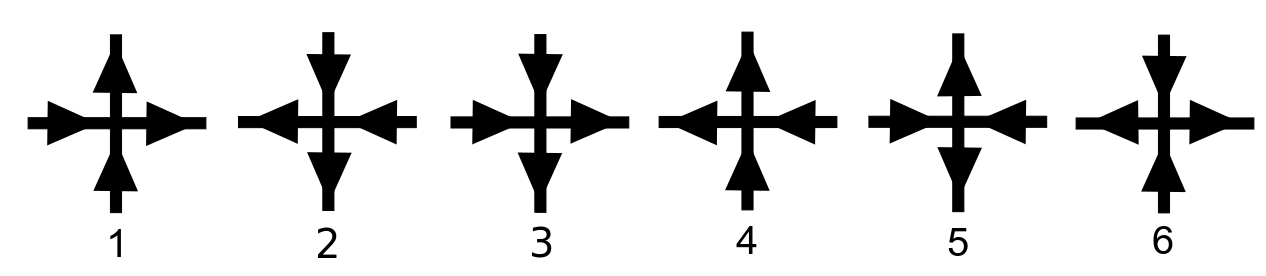
Eight-vertex Model
In statistical mechanics, the eight-vertex model is a generalization of the ice-type model, ice-type (six-vertex) models. It was discussed by T. Bill Sutherland and C. Fan & F. Y. Wu, and solved by Rodney Baxter in the zero-field case. Description As with the ice-type models, the eight-vertex model is a square lattice (group), lattice model, where each state is a configuration of arrows at a vertex. The allowed vertices have an even number of arrows pointing towards the vertex; these include the six inherited from the ice-type model (1-6), sinks (7), and sources (8). We consider a N\times N lattice, with N^2 vertices and 2N^2 edges. Imposing periodic boundary conditions requires that the states 7 and 8 occur equally often, as do states 5 and 6, and thus can be taken to have the same energy. For the zero-field case the same is true for the two other pairs of states. Each vertex j has an associated energy \epsilon_j and Boltzmann factor, Boltzmann weight : w_j=\exp\left(-\frac\rig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ice-type Model
In statistical mechanics, the ice-type models or six-vertex models are a family of vertex models for crystal lattices with hydrogen bonds. The first such model was introduced by Linus Pauling in 1935 to account for the residual entropy of water ice. Variants have been proposed as models of certain ferroelectric and antiferroelectric crystals. In 1967, Elliott H. Lieb found the exact solution to a two-dimensional ice model known as "square ice". The exact solution in three dimensions is only known for a special "frozen" state. Description An ice-type model is a lattice model defined on a lattice of coordination number 4. That is, each vertex of the lattice is connected by an edge to four "nearest neighbours". A state of the model consists of an arrow on each edge of the lattice, such that the number of arrows pointing inwards at each vertex is 2. This restriction on the arrow configurations is known as the ice rule. In graph theoretic terms, the states are Eulerian orie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg Model (quantum)
The quantum Heisenberg model, developed by Werner Heisenberg, is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spins of the magnetic systems are treated quantum mechanically. It is related to the prototypical Ising model, where at each site of a lattice, a spin \sigma_i \in \ represents a microscopic magnetic dipole to which the magnetic moment is either up or down. Except the coupling between magnetic dipole moments, there is also a multipolar version of Heisenberg model called the multipolar exchange interaction. Overview For quantum mechanical reasons (see exchange interaction or ), the dominant coupling between two dipoles may cause nearest-neighbors to have lowest energy when they are ''aligned''. Under this assumption (so that magnetic interactions only occur between adjacent dipoles) and on a 1-dimensional periodic lattice, the Hamiltonian can be written in the form :\hat H = -J \sum_^ \sig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kaup–Kupershmidt Equation
The Kaup–Kupershmidt equation (named after David J. Kaup and Boris Abram Kupershmidt) is the nonlinear fifth-order partial differential equation In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to ho ... :u_t = u_+10u_u+25u_u_x+20u^2u_x = \frac16 (6u_+60uu_+45u_x^2+40u^3)_x. It is the first equation in a hierarchy of integrable equations with the Lax operator : \partial_x^3 + 2u\partial_x + u_x, . It has properties similar (but not identical) to those of the better-known KdV hierarchy in which the Lax operator has order 2. References * External links * Partial differential equations Integrable systems {{mathanalysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hunter–Saxton Equation
In mathematical physics, the Hunter–Saxton equation : (u_t + u u_x)_x = \frac \, u_x^2 is an integrable PDE that arises in the theoretical study of nematic liquid crystals. If the molecules in the liquid crystal are initially all aligned, and some of them are then wiggled slightly, this disturbance in orientation will propagate through the crystal, and the Hunter–Saxton equation describes certain aspects of such orientation waves. Physical background In the models for liquid crystals considered here, it is assumed that there is no fluid flow, so that only the ''orientation'' of the molecules is of interest. Within the elastic continuum theory, the orientation is described by a field of unit vectors n(''x'',''y'',''z'',''t''). For nematic liquid crystals, there is no difference between orienting a molecule in the n direction or in the −n direction, and the vector field n is then called a ''director field''. The potential energy density of a director field is usually ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |