|
Linear Extension
In order theory, a branch of mathematics, a linear extension of a partial order is a total order (or linear order) that is compatible with the partial order. As a classic example, the lexicographic order of totally ordered sets is a linear extension of their product order. Definitions Linear extension of a partial order A partial order is a reflexive, transitive and antisymmetric relation. Given any partial orders \,\leq\, and \,\leq^*\, on a set X, \,\leq^*\, is a linear extension of \,\leq\, exactly when # \,\leq^*\, is a total order, and # For every x, y \in X, if x \leq y, then x \leq^* y. It is that second property that leads mathematicians to describe \,\leq^*\, as extending \,\leq. Alternatively, a linear extension may be viewed as an order-preserving bijection from a partially ordered set P to a chain C on the same ground set. Linear extension of a preorder A preorder is a reflexive and transitive relation. The difference between a preorder and a partial- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Order Theory
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary. Background and motivation Orders are everywhere in mathematics and related fields like computer science. The first order often discussed in primary school is the standard order on the natural numbers e.g. "2 is less than 3", "10 is greater than 5", or "Does Tom have fewer cookies than Sally?". This intuitive concept can be extended to orders on other sets of numbers, such as the integers and the reals. The idea of being greater than or less than another number is one of the basic intuitions of number systems in general (although one usually is also interested in the actual difference of two numbers, which is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Kazimierz Kuratowski
Kazimierz Kuratowski (; 2 February 1896 – 18 June 1980) was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics. He worked as a professor at the University of Warsaw and at the Mathematical Institute of the Polish Academy of Sciences (IM PAN). Between 1946 and 1953, he served as President of the Polish Mathematical Society. He is primarily known for his contributions to set theory, topology, measure theory and graph theory. Some of the notable mathematical concepts bearing Kuratowski's name include Kuratowski's theorem, Kuratowski closure axioms, Kuratowski-Zorn lemma and Kuratowski's intersection theorem. Life and career Early life Kazimierz Kuratowski was born in Warsaw, (then part of Congress Poland controlled by the Russian Empire), on 2 February 1896. He was a son of Marek Kuratow, a barrister, and Róża Karzewska. He completed a Warsaw secondary school, which was named after general Paweł Chrzanowski. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Linear Time
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is gene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Vertex (graph Theory)
In discrete mathematics, and more specifically in graph theory, a vertex (plural vertices) or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another. From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network is a graph in which the vertices represent concepts or classes of objects. The two vertices forming an edge are said to be the endpoints of this edge, and the edge is said to be incident to the vertices. A vertex ''w'' is said to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Directed Acyclic Graph
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called ''arcs''), with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology (evolution, family trees, epidemiology) to information science (citation networks) to computation (scheduling). Directed acyclic graphs are also called acyclic directed graphs or acyclic digraphs. Definitions A graph is formed by vertices and by edges connecting pairs of vertices, where the vertices can be any kind of object that is connected in pairs by edges. In the case of a directed graph, each edg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
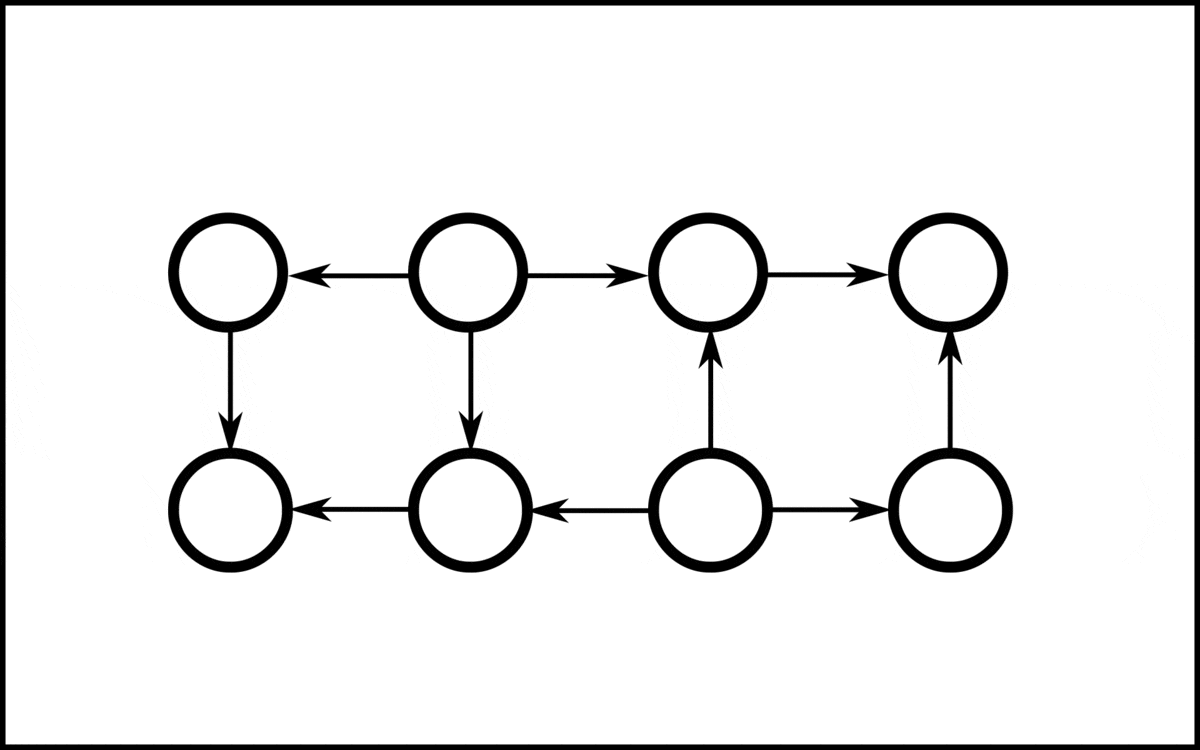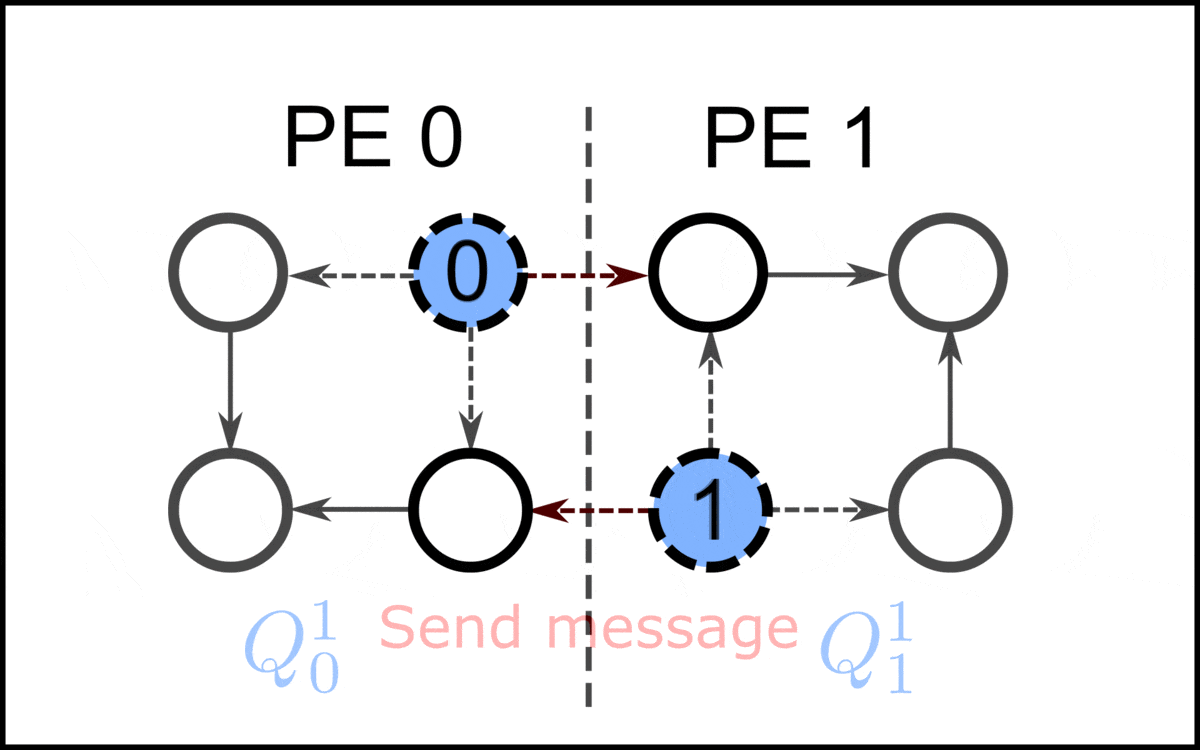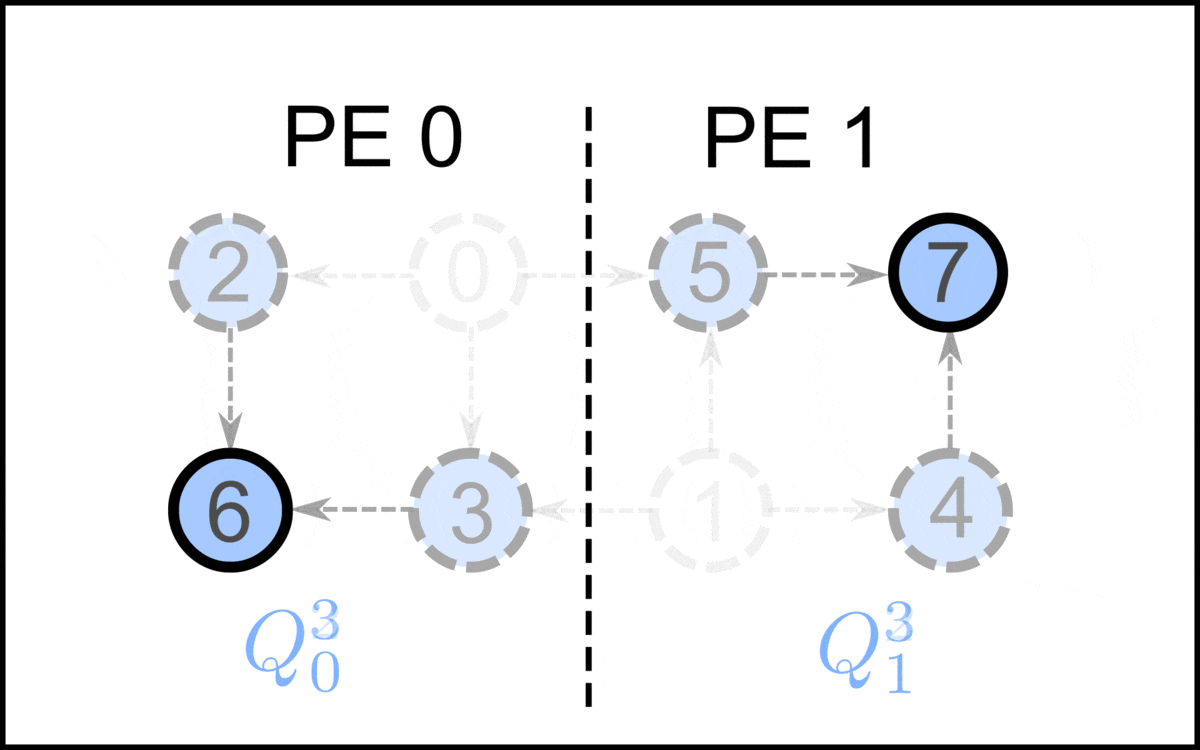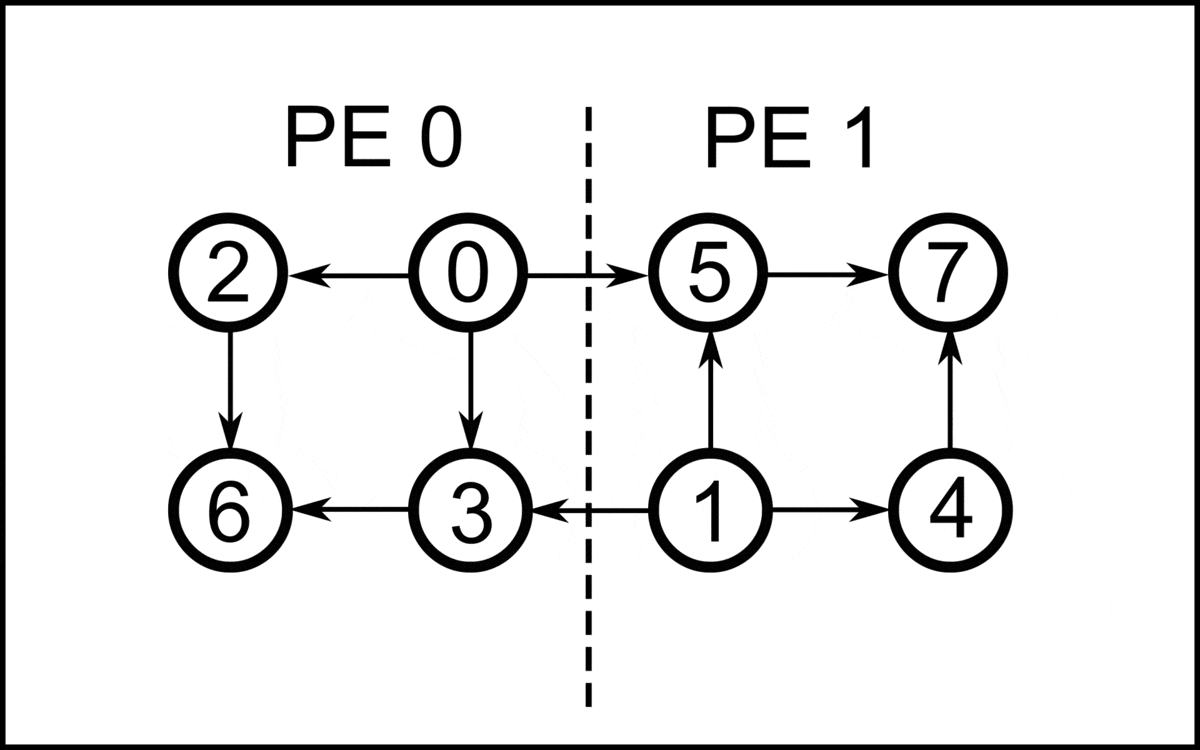 |
Topological Sorting
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge ''(u,v)'' from vertex ''u'' to vertex ''v'', ''u'' comes before ''v'' in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node ''v'' is visited only after all its dependencies are visited''.'' A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and there are linear time algorithms for constructing it. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Constructive Proof
In mathematics, a constructive proof is a method of mathematical proof, proof that demonstrates the existence of a mathematical object by creating or providing a method for creating the object. This is in contrast to a non-constructive proof (also known as an existence proof or existence theorem, ''pure existence theorem''), which proves the existence of a particular kind of object without providing an example. For avoiding confusion with the stronger concept that follows, such a constructive proof is sometimes called an effective proof. A constructive proof may also refer to the stronger concept of a proof that is valid in constructive mathematics. Constructivism (mathematics), Constructivism is a mathematical philosophy that rejects all proof methods that involve the existence of objects that are not explicitly built. This excludes, in particular, the use of the law of the excluded middle, the axiom of infinity, and the axiom of choice. Constructivism also induces a different mean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Model Theory
In mathematical logic, model theory is the study of the relationship between theory (mathematical logic), formal theories (a collection of Sentence (mathematical logic), sentences in a formal language expressing statements about a Structure (mathematical logic), mathematical structure), and their Structure (mathematical logic), models (those Structure (mathematical logic), structures in which the statements of the theory hold). The aspects investigated include the number and size of models of a theory, the relationship of different models to each other, and their interaction with the formal language itself. In particular, model theorists also investigate the sets that can be definable set, defined in a model of a theory, and the relationship of such definable sets to each other. As a separate discipline, model theory goes back to Alfred Tarski, who first used the term "Theory of Models" in publication in 1954. Since the 1970s, the subject has been shaped decisively by Saharon Shel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Well-ordering Theorem
In mathematics, the well-ordering theorem, also known as Zermelo's theorem, states that every set can be well-ordered. A set ''X'' is ''well-ordered'' by a strict total order if every non-empty subset of ''X'' has a least element under the ordering. The well-ordering theorem together with Zorn's lemma are the most important mathematical statements that are equivalent to the axiom of choice (often called AC, see also ). Ernst Zermelo introduced the axiom of choice as an "unobjectionable logical principle" to prove the well-ordering theorem. One can conclude from the well-ordering theorem that every set is susceptible to transfinite induction, which is considered by mathematicians to be a powerful technique. One famous consequence of the theorem is the Banach–Tarski paradox. History Georg Cantor considered the well-ordering theorem to be a "fundamental principle of thought". However, it is considered difficult or even impossible to visualize a well-ordering of \mathbb, the set o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Dover Publications
Dover Publications, also known as Dover Books, is an American book publisher founded in 1941 by Hayward and Blanche Cirker. It primarily reissues books that are out of print from their original publishers. These are often, but not always, books in the public domain. The original published editions may be scarce or historically significant. Dover republishes these books, making them available at a significantly reduced cost. Classic reprints Dover reprints classic works of literature, classical sheet music, and public-domain images from the 18th and 19th centuries. Dover also publishes an extensive collection of mathematical, scientific, and engineering texts. It often targets its reprints at a niche market, such as woodworking. Starting in 2015, the company branched out into graphic novel reprints, overseen by Dover acquisitions editor and former comics writer and editor Drew Ford. Most Dover reprints are photo facsimiles of the originals, retaining the original pagination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Compactness Theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model. This theorem is an important tool in model theory, as it provides a useful (but generally not effective) method for constructing models of any set of sentences that is finitely consistent. The compactness theorem for the propositional calculus is a consequence of Tychonoff's theorem (which says that the product of compact spaces is compact) applied to compact Stone spaces, hence the theorem's name. Likewise, it is analogous to the finite intersection property characterization of compactness in topological spaces: a collection of closed sets in a compact space has a non-empty intersection if every finite subcollection has a non-empty intersection. The compactness theorem is one of the two key properties, along with the downward Löwenheim–Skolem theorem, that is used in Lindström's theorem to characterize first-ord ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |