|
Least Absolute Values
Least absolute deviations (LAD), also known as least absolute errors (LAE), least absolute residuals (LAR), or least absolute values (LAV), is a statistical optimality criterion and a statistical optimization technique based on minimizing the sum of absolute deviations (also ''sum of absolute residuals'' or ''sum of absolute errors'') or the ''L''1 norm of such values. It is analogous to the least squares technique, except that it is based on ''absolute values'' instead of squared values. It attempts to find a function which closely approximates a set of data by minimizing residuals between points generated by the function and corresponding data points. The LAD estimate also arises as the maximum likelihood estimate if the errors have a Laplace distribution. It was introduced in 1757 by Roger Joseph Boscovich. Formulation Suppose that the data set consists of the points (''x''''i'', ''y''''i'') with ''i'' = 1, 2, ..., ''n''. We want to find a function ''f'' such that f(x_i)\ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimality Criterion
Optimality may refer to: * Mathematical optimization * Optimality theory Optimality theory (frequently abbreviated OT) is a linguistic model proposing that the observed forms of language arise from the optimal satisfaction of conflicting constraints. OT differs from other approaches to phonological analysis, which ty ... in linguistics * Optimality model, approach in biology See also * * Optimism (other) * Optimist (other) * Optimistic (other) * Optimization (other) * Optimum (other) {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iteratively Re-weighted Least Squares
The method of iteratively reweighted least squares (IRLS) is used to solve certain optimization problems with objective functions of the form of a ''p''-norm: \mathop_ \sum_^n \big, y_i - f_i (\boldsymbol\beta) \big, ^p, by an iterative method in which each step involves solving a weighted least squares problem of the form:C. Sidney Burrus, Iterative Reweighted Least Squares' \boldsymbol\beta^ = \underset \sum_^n w_i (\boldsymbol\beta^) \big, y_i - f_i (\boldsymbol\beta) \big, ^2. IRLS is used to find the maximum likelihood estimates of a generalized linear model, and in robust regression to find an M-estimator, as a way of mitigating the influence of outliers in an otherwise normally-distributed data set, for example, by minimizing the least absolute errors rather than the least square errors. One of the advantages of IRLS over linear programming and convex programming is that it can be used with Gauss–Newton and Levenberg–Marquardt numerical algorithms. Exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Median
In geometry, the geometric median of a discrete point set in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances or absolute differences for one-dimensional data. It is also known as the spatial median, Euclidean minisum point, Torricelli point, or 1-median. It provides a measure of central tendency in higher dimensions and it is a standard problem in facility location, i.e., locating a facility to minimize the cost of transportation. The geometric median is an important estimator of location in statistics, because it minimizes the sum of the ''L''2 distances of the samples. It is to be compared to the mean, which minimizes the sum of the ''squared'' ''L''2 distances; and to the coordinate-wise median which minimizes the sum of the ''L''1 distances. The more general ''k''-median problem asks for the location of ''k'' cluster centers minimizing the sum o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lasso (statistics)
In statistics and machine learning, lasso (least absolute shrinkage and selection operator; also Lasso, LASSO or L1 regularization) is a regression analysis method that performs both variable selection and Regularization (mathematics), regularization in order to enhance the prediction accuracy and interpretability of the resulting statistical model. The lasso method assumes that the coefficients of the linear model are sparse, meaning that few of them are non-zero. It was originally introduced in geophysics, and later by Robert Tibshirani, who coined the term. Lasso was originally formulated for linear regression models. This simple case reveals a substantial amount about the estimator. These include its relationship to ridge regression and best subset selection and the connections between lasso coefficient estimates and so-called soft thresholding. It also reveals that (like standard linear regression) the coefficient estimates do not need to be unique if covariates are collinear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, Mathematical finance, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the Problem solving, answer to a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, the following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be Prior probability, priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Statistics & Data Analysis
''Computational Statistics & Data Analysis'' is a monthly peer-reviewed scientific journal covering research on and applications of computational statistics and data analysis. The journal was established in 1983 and is the official journal of the International Association for Statistical Computing, a section of the International Statistical Institute The International Statistical Institute (ISI) is a professional association of statisticians. At a meeting of the Jubilee Meeting of the Royal Statistical Society, statisticians met and formed the agreed statues of the International Statistical .... See also * List of statistics journals References External links * International Statistical Institute Statistics journals Academic journals established in 1983 Monthly journals English-language journals Elsevier academic journals * {{compu-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, Mathematical finance, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the Problem solving, answer to a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, the following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be Prior probability, priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantile Regression
Quantile regression is a type of regression analysis used in statistics and econometrics. Whereas the method of least squares estimates the conditional ''mean'' of the response variable across values of the predictor variables, quantile regression estimates the conditional ''median'' (or other '' quantiles'') of the response variable. here is also a method for predicting the conditional geometric mean of the response variable, Tofallis (2015). "A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation", ''Journal of the Operational Research Society'', 66(8):1352-1362/ref>.] Quantile regression is an extension of linear regression used when the conditions of linear regression are not met. Advantages and applications One advantage of quantile regression relative to ordinary least squares regression is that the quantile regression estimates are more robust against outliers in the response measurements. However, the main attraction of quantile reg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
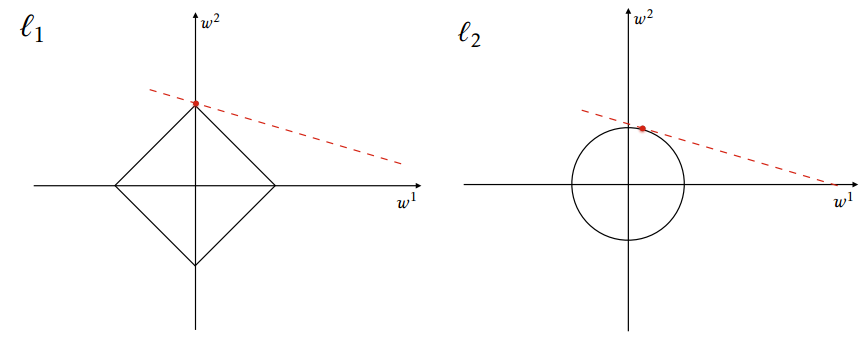
Least Absolute Deviations Regression Method Diagram
The degrees of comparison of adjectives and adverbs are the various forms taken by adjectives and adverbs when used to compare two entities (comparative degree), three or more entities (superlative degree), or when not comparing entities (positive degree) in terms of a certain property or way of doing something. The usual degrees of comparison are the ''positive'', which denotes a certain property or a certain way of doing something without comparing (as with the English words ''big'' and ''fully''); the ''comparative degree'', which indicates ''greater'' degree (e.g. ''bigger'' and ''more fully'' omparative of superiorityor ''as big'' and ''as fully'' omparative of equalityor ''less big'' and ''less fully'' omparative of inferiority; and the ''superlative'', which indicates ''greatest'' degree (e.g. ''biggest'' and ''most fully'' uperlative of superiorityor ''least big'' and ''least fully'' uperlative of inferiority. Some languages have forms indicating a very large degree ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomical Journal
''The Astronomical Journal'' (often abbreviated ''AJ'' in scientific papers and references) is a peer-reviewed monthly scientific journal owned by the American Astronomical Society (AAS) and currently published by IOP Publishing. It is one of the premier journals for astronomy in the world. Until 2008, the journal was published by the University of Chicago Press on behalf of the AAS. The reasons for the change to the IOP were given by the society as the desire of the University of Chicago Press to revise its financial arrangement and their plans to change from the particular software that had been developed in-house. The other two publications of the society, the ''Astrophysical Journal'' and its supplement series, followed in January 2009. The journal was established in 1849 by Benjamin A. Gould. It ceased publication in 1861 due to the American Civil War, but resumed in 1885. Between 1909 and 1941 the journal was edited in Albany, New York. In 1941, editor Benjamin Boss arrange ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent And Independent Variables
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, on the other hand, are not seen as depending on any other variable in the scope of the experiment in question. Rather, they are controlled by the experimenter. In pure mathematics In mathematics, a function (mathematics), function is a rule for taking an input (in the simplest case, a number or set of numbers)Carlson, Robert. A concrete introduction to real analysis. CRC Press, 2006. p.183 and providing an output (which may also be a number). A symbol that stands for an arbitrary input is called an independent variable, while a symbol that stands for an arbitrary output is called a dependent variable. The most common symbol for the input is , and the most common symbol for the o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |