|
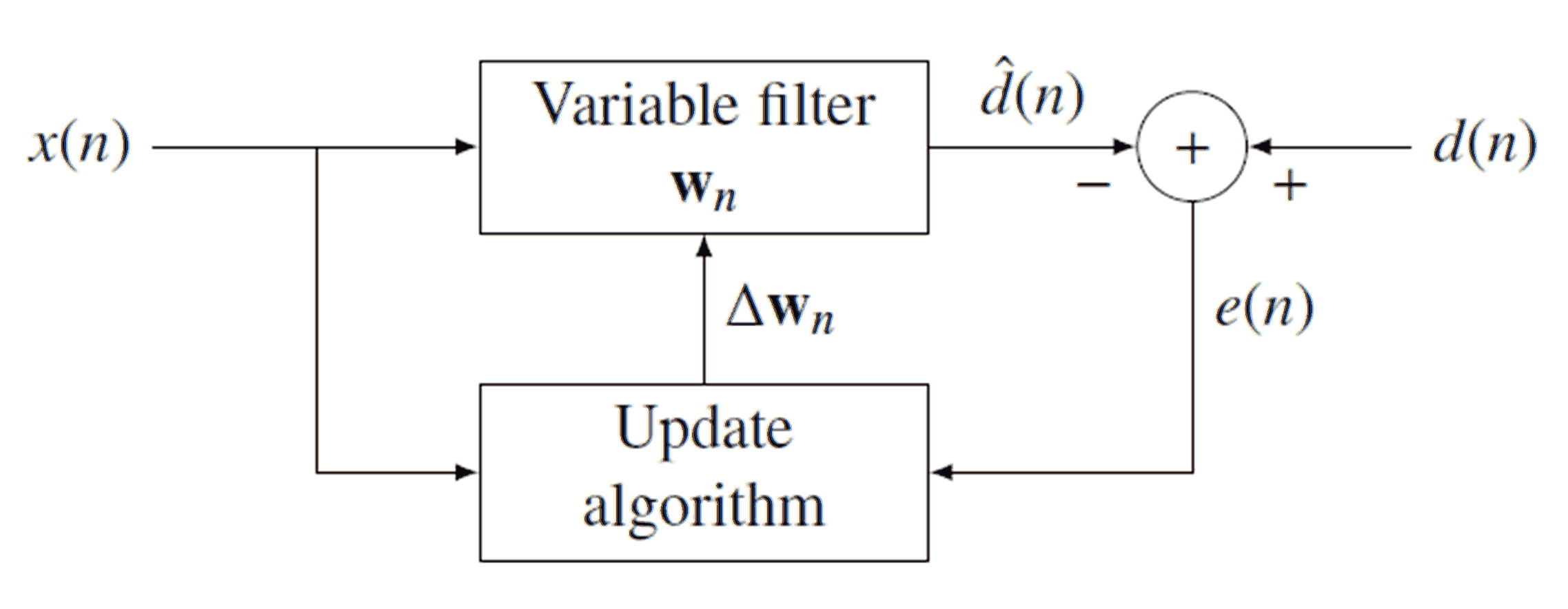
Least Mean Squares
Least mean squares (LMS) algorithms are a class of adaptive filter used to mimic a desired filter by finding the filter coefficients that relate to producing the least mean square of the error signal (difference between the desired and the actual signal). It is a stochastic gradient descent method in that the filter is only adapted based on the error at the current time. It was invented in 1960 by Stanford University professor Bernard Widrow and his first Ph.D. student, Ted Hoff, based on their research in single-layer neural networks ( ADALINE). Specifically, they used gradient descent to train ADALINE to recognize patterns, and called the algorithm " delta rule". They then applied the rule to filters, resulting in the LMS algorithm. Problem formulation The picture shows the various parts of the filter. x is the input signal, which is then transformed by an unknown filter h that we wish to match using \hat h. The output from the unknown filter is y, which is then interfere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adaptive Filter
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorithms, almost all adaptive filters are digital filters. Adaptive filters are required for some applications because some parameters of the desired processing operation (for instance, the locations of reflective surfaces in a reverberant space) are not known in advance or are changing. The closed loop adaptive filter uses feedback in the form of an error signal to refine its transfer function. Generally speaking, the closed loop adaptive process involves the use of a cost function, which is a criterion for optimum performance of the filter, to feed an algorithm, which determines how to modify filter transfer function to minimize the cost on the next iteration. The most common cost function is the mean square of the error signal. As the pow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matched Filter
In signal processing, the output of the matched filter is given by correlating a known delayed signal, or ''template'', with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template. The matched filter is the optimal linear filter for maximizing the signal-to-noise ratio (SNR) in the presence of additive stochastic noise. Matched filters are commonly used in radar, in which a known signal is sent out, and the reflected signal is examined for common elements of the out-going signal. Pulse compression is an example of matched filtering. It is so called because the impulse response is matched to input pulse signals. Two-dimensional matched filters are commonly used in image processing, e.g., to improve the SNR of X-ray observations. Additional applications of note are in seismology and gravitational-wave astronomy. Matched filtering is a demodulation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Adaptive Filter
In signal processing, a kernel adaptive filter is a type of nonlinear adaptive filter. An adaptive filter is a filter that adapts its transfer function to changes in signal properties over time by minimizing an error or loss function that characterizes how far the filter deviates from ideal behavior. The adaptation process is based on learning from a sequence of signal samples and is thus an online algorithm. A nonlinear adaptive filter is one in which the transfer function is nonlinear. Kernel adaptive filters implement a nonlinear transfer function using kernel methods. In these methods, the signal is mapped to a high-dimensional linear feature space and a nonlinear function is approximated as a sum over kernels, whose domain is the feature space. If this is done in a reproducing kernel Hilbert space, a kernel method can be a universal approximator for a nonlinear function. Kernel methods have the advantage of having convex loss functions, with no local minima, and of being only m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero-forcing Equalizer
The zero-forcing equalizer is a form of linear equalization algorithm used in communication systems which applies the inverse of the frequency response of the channel. This form of equalizer was first proposed by Robert Lucky. The zero-forcing equalizer applies the inverse of the channel frequency response to the received signal, to restore the signal after the channel. It has many useful applications. For example, it is studied heavily for IEEE 802.11n (MIMO) where knowing the channel allows recovery of the two or more streams which will be received on top of each other on each antenna. The name ''zero-forcing corresponds'' to bringing down the intersymbol interference (ISI) to zero in a noise-free case. This will be useful when ISI is significant compared to noise. For a channel with frequency response F(f) the zero-forcing equalizer C(f) is constructed by C(f) = 1/F(f). Thus the combination of channel and equalizer gives a flat frequency response and linear phase F(f)C(f) = 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multidelay Block Frequency Domain Adaptive Filter
The multidelay block frequency domain adaptive filter (MDF) algorithm is a block-based frequency domain implementation of the (normalised) Least mean squares filter (LMS) algorithm. Introduction The MDF algorithm is based on the fact that convolutions may be efficiently computed in the frequency domain (thanks to the fast Fourier transform). However, the algorithm differs from the fast LMS algorithm in that block size it uses may be smaller than the filter length. If both are equal, then MDF reduces to the FLMS algorithm. The advantages of MDF over the (N)LMS algorithm are: * Lower algorithmic complexity * Partial de-correlation of the input (which 'may' lead to faster convergence) Variable definitions Let N be the length of the processing blocks, K be the number of blocks and \mathbf denote the 2Nx2N Fourier transform matrix. The variables are defined as: : \underline(\ell) = \mathbf\left \mathbf_, e(\ell N),\dots,e(\ell N-N-1) \rightT : \underline_k(\ell) = \mathrm \left ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarities Between Wiener And LMS
The Least mean squares filter solution converges to the Wiener filter solution, assuming that the unknown system is LTI and the noise is stationary. Both filters can be used to identify the impulse response of an unknown system, knowing only the original input signal and the output of the unknown system. By relaxing the error criterion to reduce current sample error instead of minimizing the total error over all of n, the LMS algorithm can be derived from the Wiener filter. Derivation of the Wiener filter for system identification Given a known input signal s /math>, the output of an unknown LTI system x /math> can be expressed as: x = \sum_^ h_ks -k+ w /math> where h_k is an unknown filter tap coefficients and w /math> is noise. The model system \hat /math>, using a Wiener filter solution with an order N, can be expressed as: \hat = \sum_^\hat_ks -k/math> where \hat_k are the filter tap coefficients to be determined. The error between the model and the unknown system ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The method is widely used in areas such as regression analysis, curve fitting and data modeling. The least squares method can be categorized into linear and nonlinear forms, depending on the relationship between the model parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. History Founding The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursive Least Squares
Recursive least squares (RLS) is an adaptive filter algorithm that recursively finds the coefficients that minimize a Weighted least squares, weighted linear least squares Loss function, cost function relating to the input signals. This approach is in contrast to other algorithms such as the least mean squares (LMS) that aim to reduce the mean square error. In the derivation of the RLS, the input signals are considered deterministic system (mathematics), deterministic, while for the LMS and similar algorithms they are considered stochastic. Compared to most of its competitors, the RLS exhibits extremely fast convergence. However, this benefit comes at the cost of high computational complexity. Motivation RLS was discovered by Carl Friedrich Gauss, Gauss but lay unused or ignored until 1950 when Plackett rediscovered the original work of Gauss from 1821. In general, the RLS can be used to solve any problem that can be solved by adaptive filters. For example, suppose that a signal d( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Learning Rate
In machine learning and statistics, the learning rate is a tuning parameter in an optimization algorithm that determines the step size at each iteration while moving toward a minimum of a loss function. Since it influences to what extent newly acquired information overrides old information, it metaphorically represents the speed at which a machine learning model "learns". In the adaptive control literature, the learning rate is commonly referred to as gain. In setting a learning rate, there is a trade-off between the rate of convergence and overshooting. While the descent direction is usually determined from the gradient of the loss function, the learning rate determines how big a step is taken in that direction. A too high learning rate will make the learning jump over minima but a too low learning rate will either take too long to converge or get stuck in an undesirable local minimum. In order to achieve faster convergence, prevent oscillations and getting stuck in undesi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace (linear Algebra)
In linear algebra, the trace of a square matrix , denoted , is the sum of the elements on its main diagonal, a_ + a_ + \dots + a_. It is only defined for a square matrix (). The trace of a matrix is the sum of its eigenvalues (counted with multiplicities). Also, for any matrices and of the same size. Thus, similar matrices have the same trace. As a consequence, one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the row and column of . The entries of can be real numbers, complex numbers, or more generally elements of a field . The trace is not defined for non-square matrices. Example Let be a matrix, with \m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
White Noise
In signal processing, white noise is a random signal having equal intensity at different frequencies, giving it a constant power spectral density. The term is used with this or similar meanings in many scientific and technical disciplines, including physics, acoustical engineering, telecommunications, and statistical forecasting. White noise refers to a statistical model for signals and signal sources, not to any specific signal. White noise draws its name from white light, although light that appears white generally does not have a flat power spectral density over the visible band. In discrete time, white noise is a discrete signal whose samples are regarded as a sequence of serially uncorrelated random variables with zero mean and finite variance; a single realization of white noise is a random shock. In some contexts, it is also required that the samples be independent and have identical probability distribution (in other words independent and identically distribu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |