|
Latent Variable Model
A latent variable model is a statistical model that relates a set of observable variables (also called ''manifest variables'' or ''indicators'') to a set of latent variables. Latent variable models are applied across a wide range of fields such as biology, computer science, and social science. Common use cases for latent variable models include applications in psychometrics (e.g., summarizing responses to a set of survey questions with a factor analysis model positing a smaller number of psychological attributes, such as the trait extraversion, that are presumed to cause the survey question responses), and natural language processing (e.g., a topic model summarizing a corpus of texts with a number of "topics"). It is assumed that the responses on the indicators or manifest variables are the result of an individual's position on the latent variable(s), and that the manifest variables have nothing in common after controlling for the latent variable ( local independence). Different ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Model
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of Sample (statistics), sample data (and similar data from a larger Statistical population, population). A statistical model represents, often in considerably idealized form, the Data generating process, data-generating process. When referring specifically to probability, probabilities, the corresponding term is probabilistic model. All Statistical hypothesis testing, statistical hypothesis tests and all Estimator, statistical estimators are derived via statistical models. More generally, statistical models are part of the foundation of statistical inference. A statistical model is usually specified as a mathematical relationship between one or more random variables and other non-random variables. As such, a statistical model is "a formal representation of a theory" (Herman J. Adèr, Herman Adèr quoting Kenneth A. Bollen, Kenneth Bollen). Introduction Informally, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Class Analysis
In statistics, a latent class model (LCM) is a model for clustering multivariate discrete data. It assumes that the data arise from a mixture of discrete distributions, within each of which the variables are independent. It is called a latent class model because the class to which each data point belongs is unobserved, or latent. Latent class analysis (LCA) is a subset of structural equation modeling, used to find groups or subtypes of cases in multivariate categorical data. These subtypes are called "latent classes".Lazarsfeld, P.F. and Henry, N.W. (1968) ''Latent structure analysis''. Boston: Houghton Mifflin Confronted with a situation as follows, a researcher might choose to use LCA to understand the data: Imagine that symptoms a-d have been measured in a range of patients with diseases X, Y, and Z, and that disease X is associated with the presence of symptoms a, b, and c, disease Y with symptoms b, c, d, and disease Z with symptoms a, c and d. The LCA will attempt to detect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Least Squares Path Modeling
The partial least squares path modeling or partial least squares structural equation modeling (PLS-PM, PLS-SEM) is a method for structural equation modeling that allows estimation of complex cause-effect relationships in path models with latent variables. Overview PLS-PM is a component-based estimation approach that differs from the covariance-based structural equation modeling. Unlike covariance-based approaches to structural equation modeling, PLS-PM does not fit a common factor model to the data, it rather fits a composite model. In doing so, it maximizes the amount of variance explained (though what this means from a statistical point of view is unclear and PLS-PM users do not agree on how this goal might be achieved). In addition, by an adjustment PLS-PM is capable of consistently estimating certain parameters of common factor models as well, through an approach called consistent PLS-PM (PLSc-PM). A further related development is factor-based PLS-PM (PLSF), a variation of w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hidden Markov Model
A hidden Markov model (HMM) is a Markov model in which the observations are dependent on a latent (or ''hidden'') Markov process (referred to as X). An HMM requires that there be an observable process Y whose outcomes depend on the outcomes of X in a known way. Since X cannot be observed directly, the goal is to learn about state of X by observing Y. By definition of being a Markov model, an HMM has an additional requirement that the outcome of Y at time t = t_0 must be "influenced" exclusively by the outcome of X at t = t_0 and that the outcomes of X and Y at t < t_0 must be conditionally independent of at given at time . Estimation of the parameters in an HMM can be performed using maximum likelihood estimation. For linear chain HMMs, the Baum–Welch algorithm can be used to estimate parameters. Hidden Markov models are known for their applications to thermodynamics, statistical mechanics, physics, chem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confirmatory Factor Analysis
In statistics, confirmatory factor analysis (CFA) is a special form of factor analysis, most commonly used in social science research.Kline, R. B. (2010). ''Principles and practice of structural equation modeling (3rd ed.).'' New York, New York: Guilford Press. It is used to test whether measures of a wikt:construct, construct are consistent with a researcher's understanding of the nature of that construct (or factor). As such, the objective of confirmatory factor analysis is to test whether the data fit a hypothesized measurement model. This hypothesized model is based on theory and/or previous analytic research. CFA was first developed by Karl Gustav Jöreskog, Jöreskog (1969) and has built upon and replaced older methods of analyzing construct validity such as the Multitrait-Multimethod Matrix, MTMM Matrix as described in Campbell & Fiske (1959). In confirmatory factor analysis, the researcher first develops a hypothesis about what factors they believe are underlying the measure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multinomial Distribution
In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a ''k''-sided die rolled ''n'' times. For ''n'' statistical independence, independent trials each of which leads to a success for exactly one of ''k'' categories, with each category having a given fixed success probability, the multinomial distribution gives the probability of any particular combination of numbers of successes for the various categories. When ''k'' is 2 and ''n'' is 1, the multinomial distribution is the Bernoulli distribution. When ''k'' is 2 and ''n'' is bigger than 1, it is the binomial distribution. When ''k'' is bigger than 2 and ''n'' is 1, it is the categorical distribution. The term "multinoulli" is sometimes used for the categorical distribution to emphasize this four-way relationship (so ''n'' determines the suffix, and ''k'' the prefix). The Bernoulli distribution models the outcome of a si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
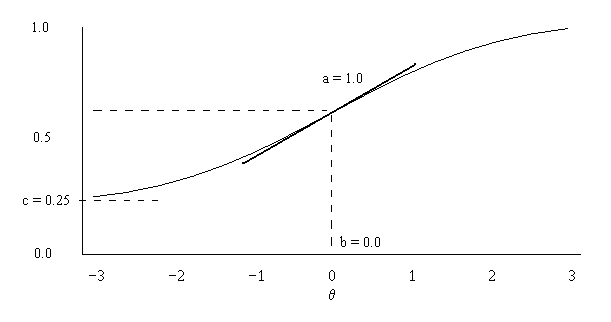
Latent Trait Analysis
In psychometrics, item response theory (IRT, also known as latent trait theory, strong true score theory, or modern mental test theory) is a paradigm for the design, analysis, and scoring of tests, questionnaires, and similar instruments measuring abilities, attitudes, or other variables. It is a theory of testing based on the relationship between individuals' performances on a test item and the test takers' levels of performance on an overall measure of the ability that item was designed to measure. Several different statistical models are used to represent both item and test taker characteristics. Unlike simpler alternatives for creating scales and evaluating questionnaire responses, it does not assume that each item is equally difficult. This distinguishes IRT from, for instance, Likert scaling, in which ''"''All items are assumed to be replications of each other or in other words items are considered to be parallel instruments". By contrast, item response theory treats the diff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixture Models
In chemistry, a mixture is a material made up of two or more different chemical substances which can be separated by physical method. It is an impure substance made up of 2 or more elements or compounds mechanically mixed together in any proportion. A mixture is the physical combination of two or more substances in which the identities are retained and are mixed in the form of solutions, suspensions or colloids. Mixtures are one product of mechanically blending or mixing chemical substances such as elements and compounds, without chemical bonding or other chemical change, so that each ingredient substance retains its own chemical properties and makeup. Despite the fact that there are no chemical changes to its constituents, the physical properties of a mixture, such as its melting point, may differ from those of the components. Some mixtures can be separated into their components by using physical (mechanical or thermal) means. Azeotropes are one kind of mixture that usually po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rasch Model
The Rasch model, named after Georg Rasch, is a psychometric model for analyzing categorical data, such as answers to questions on a reading assessment or questionnaire responses, as a function of the trade-off between the respondent's abilities, attitudes, or personality traits, and the item difficulty. For example, they may be used to estimate a student's reading ability or the extremity of a person's attitude to capital punishment from responses on a questionnaire. In addition to psychometrics and educational research, the Rasch model and its extensions are used in other areas, including the health profession, agriculture, and market research. The mathematical theory underlying Rasch models is a special case of item response theory. However, there are important differences in the interpretation of the model parameters and its philosophical implications that separate proponents of the Rasch model from the item response modeling tradition. A central aspect of this divide relates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Profile Analysis
Latency or latent may refer to: Engineering * Latency (engineering), a measure of the time delay experienced by a system ** Latency (audio), the delay between the moment an audio signal is triggered and the moment it is produced or received ** Mechanical latency Music * The Latency, a Canadian pop rock band Psychology * Latency stage, a stage of psychosexual development in a child See also * * {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Observable Variable
In physics, an observable is a physical property or physical quantity that can be measured. In classical mechanics, an observable is a real-valued "function" on the set of all possible system states, e.g., position and momentum. In quantum mechanics, an observable is an operator, or gauge, where the property of the quantum state can be determined by some sequence of operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value. Physically meaningful observables must also satisfy transformation laws that relate observations performed by different observers in different frames of reference. These transformation laws are automorphisms of the state space, that is bijective transformations that preserve certain mathematical properties of the space in question. Quantum mechanics In quantum mechanics, observables manifest as self-adjoint operators on a separable complex Hilbert space repr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |