|
Knot Complement
In mathematics, the knot complement of a tame knot ''K'' is the space where the knot is not. If a knot is embedded in the 3-sphere, then the complement is the 3-sphere minus the space near the knot. To make this precise, suppose that ''K'' is a knot in a three-manifold ''M'' (most often, ''M'' is the 3-sphere). Let ''N'' be a tubular neighborhood of ''K''; so ''N'' is a solid torus. The knot complement is then the complement of ''N'', :X_K = M - \mbox(N). The knot complement ''XK'' is a compact 3-manifold; the boundary of ''XK'' and the boundary of the neighborhood ''N'' are homeomorphic to a two-torus In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu .... Sometimes the ambient manifold ''M'' is understood to be the 3-sphere. Context is needed to determine the usage. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unknot
In the knot theory, mathematical theory of knots, the unknot, not knot, or trivial knot, is the least knotted of all knots. Intuitively, the unknot is a closed loop of rope without a Knot (mathematics), knot tied into it, unknotted. To a knot theorist, an unknot is any embedding, embedded Topological sphere, topological circle in the 3-sphere that is ambient isotopy, ambient isotopic (that is, deformable) to a geometrically round circle, the standard unknot. The unknot is the only knot that is the boundary of an embedded disk (mathematics), disk, which gives the characterization that only unknots have Seifert surface, Seifert genus 0. Similarly, the unknot is the identity element with respect to the knot sum operation. Unknotting problem Deciding if a particular knot is the unknot was a major driving force behind knot invariants, since it was thought this approach would possibly give an efficient algorithm to unknotting problem, recognize the unknot from some presentation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link (knot Theory)
In mathematical knot theory, a link is a collection of knots that do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a ''trivial'' reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link. For example, a co-dimension 2 link in 3-dimensional space is a subspace of 3-dimensional Euclidean space (or often the 3-sphere) whose connected components are homeomorphic to circles. The simplest nontrivial example of a link with more than one component is called the Hopf link, which consists of two circles (or unknots) linked together once. The circles in the Borromean rings are collectively linked despite the fact that no two of them are directly linked. The Borromean rings thus form a Brunnian link and in fact constitu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
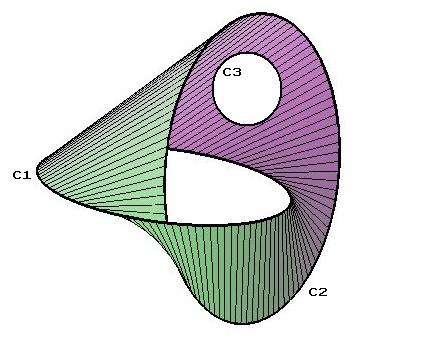
Seifert Surface
In mathematics, a Seifert surface (named after German mathematician Herbert Seifert) is an orientable surface whose boundary is a given knot or link. Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface. Seifert surfaces are also interesting in their own right, and the subject of considerable research. Specifically, let ''L'' be a tame oriented knot or link in Euclidean 3-space (or in the 3-sphere). A Seifert surface is a compact, connected, oriented surface ''S'' embedded in 3-space whose boundary is ''L'' such that the orientation on ''L'' is just the induced orientation from ''S''. Note that any compact, connected, oriented surface with nonempty boundary in Euclidean 3-space is the Seifert surface associated to its boundary link. A single knot or link can have many different inequivalent Seifert surfaces. A Seifert surface must be oriented. It is possi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Genus
In mathematics, a Seifert surface (named after German mathematician Herbert Seifert) is an orientable surface whose boundary is a given knot or link. Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface. Seifert surfaces are also interesting in their own right, and the subject of considerable research. Specifically, let ''L'' be a tame oriented knot or link in Euclidean 3-space (or in the 3-sphere). A Seifert surface is a compact, connected, oriented surface ''S'' embedded in 3-space whose boundary is ''L'' such that the orientation on ''L'' is just the induced orientation from ''S''. Note that any compact, connected, oriented surface with nonempty boundary in Euclidean 3-space is the Seifert surface associated to its boundary link. A single knot or link can have many different inequivalent Seifert surfaces. A Seifert surface must be oriented. It is possible to ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link (knot Theory)
In mathematical knot theory, a link is a collection of knots that do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a ''trivial'' reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link. For example, a co-dimension 2 link in 3-dimensional space is a subspace of 3-dimensional Euclidean space (or often the 3-sphere) whose connected components are homeomorphic to circles. The simplest nontrivial example of a link with more than one component is called the Hopf link, which consists of two circles (or unknots) linked together once. The circles in the Borromean rings are collectively linked despite the fact that no two of them are directly linked. The Borromean rings thus form a Brunnian link and in fact constitu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Haken Manifolds
In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface. Sometimes one considers only orientable Haken manifolds, in which case a Haken manifold is a compact, orientable, irreducible 3-manifold that contains an orientable, incompressible surface. A 3-manifold finitely covered by a Haken manifold is said to be virtually Haken. The Virtually Haken conjecture asserts that every compact, irreducible 3-manifold with infinite fundamental group is virtually Haken. This conjecture was proven by Ian Agol. Haken manifolds were introduced by . proved that Haken manifolds have a hierarchy, where they can be split up into 3-balls along incompressible surfaces. Haken also showed that there was a finite procedure to find an incompressible surface if the 3-manifold had one. gave an algorithm to determine if a 3-manifold was Haken. Normal surfaces are ubiquitous in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homeomorphic
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. Very roughly speaking, a topological space is a geometric object, and a homeomorphism results from a continuous deformation of the object into a new shape. Thus, a square and a circle are homeomorphic to each other, but a sphere and a torus are not. However, this description can be misleading. Some continuous deformations do not produce homeomorphisms, such as the deformation of a li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gordon–Luecke Theorem
In mathematics, the Gordon–Luecke theorem on knot complements states that if the complements of two tame knots are homeomorphic, then the knots are equivalent. In particular, any homeomorphism between knot complements must take a meridian to a meridian. The theorem is usually stated as "knots are determined by their complements"; however this is slightly ambiguous as it considers two knots to be equivalent if there is a self-homeomorphism taking one knot to the other. Thus mirror images are neglected. Often two knots are considered equivalent if they are '' isotopic''. The correct version in this case is that if two knots have complements which are orientation-preserving homeomorphic, then they are isotopic. These results follow from the following (also called the Gordon–Luecke theorem): no nontrivial Dehn surgery on a nontrivial knot in the 3-sphere can yield the 3-sphere. The theorem was proved by Cameron Gordon and John Luecke. Essential ingredients of the proo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Group
In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot ''K'' is defined as the fundamental group of the knot complement of ''K'' in R3, :\pi_1(\mathbb^3 \setminus K). Other conventions consider knots to be embedded in the 3-sphere, in which case the knot group is the fundamental group of its complement in S^3. Properties Two equivalent knots have isomorphic knot groups, so the knot group is a knot invariant and can be used to distinguish between certain pairs of inequivalent knots. This is because an equivalence between two knots is a self-homeomorphism of \mathbb^3 that is isotopic to the identity and sends the first knot onto the second. Such a homeomorphism restricts onto a homeomorphism of the complements of the knots, and this restricted homeomorphism induces an isomorphism of fundamental groups. However, it is possible for two inequivalent knots to have isomorphic knot groups (see below for an example). The abelia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Invariant
In the mathematical field of knot theory, a knot invariant is a quantity (in a broad sense) defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers (algebraic), but invariants can range from the simple, such as a yes/no answer, to those as complex as a homology theory (for example, "a ''knot invariant'' is a rule that assigns to any knot a quantity such that if and are equivalent then ."). Research on invariants is not only motivated by the basic problem of distinguishing one knot from another but also to understand fundamental properties of knots and their relations to other branches of mathematics. Knot invariants are thus used in knot classification,Purcell, Jessica (2020). ''Hyperbolic Knot Theory'', p.7. American Mathematical Society. "A ''knot invariant'' is a function from the set of knots to some other set whose value depends only on the equiva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homeomorphism
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. Very roughly speaking, a topological space is a geometric object, and a homeomorphism results from a continuous deformation of the object into a new shape. Thus, a square and a circle are homeomorphic to each other, but a sphere and a torus are not. However, this description can be misleading. Some continuous deformations do not produce homeomorphisms, such as the deformation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |