|
Kinematic Theory Of Diffraction
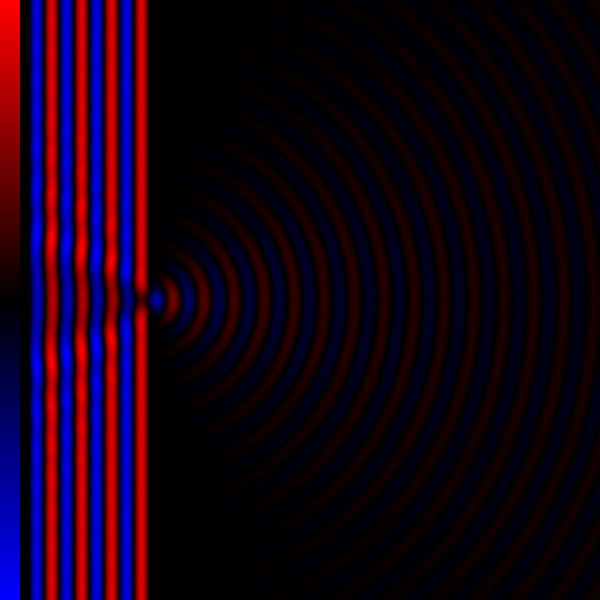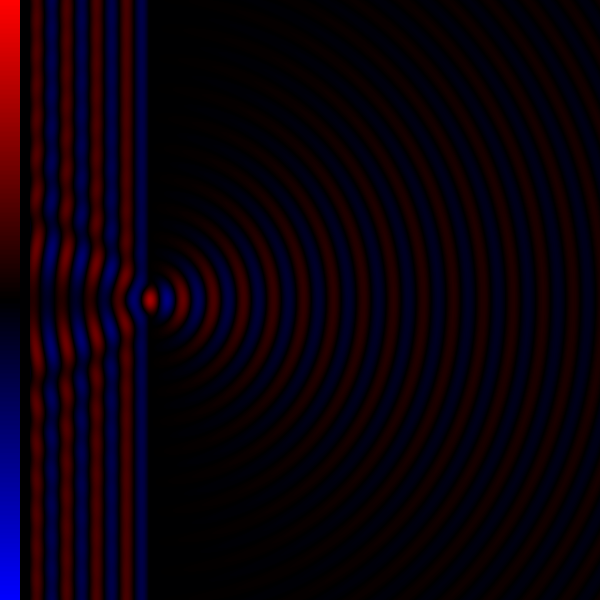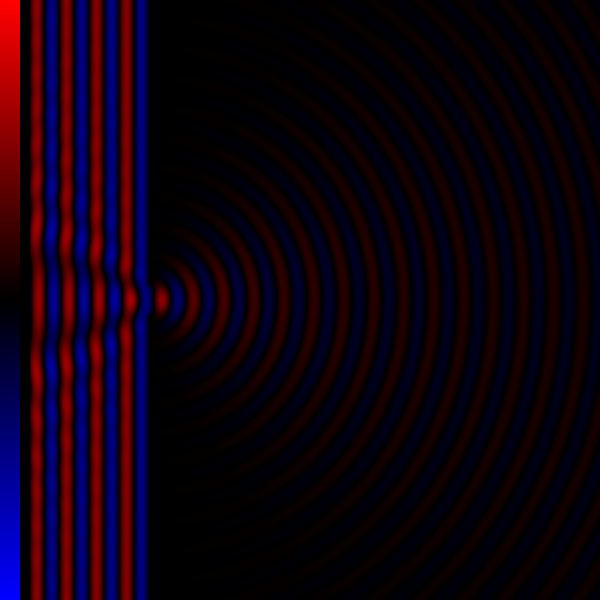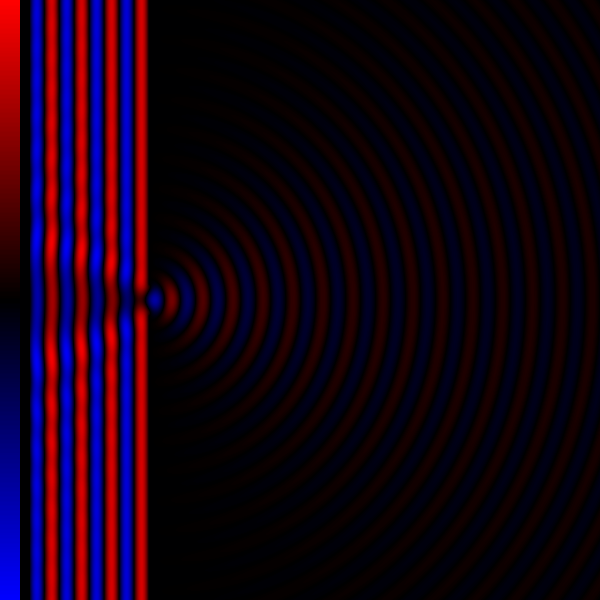
Diffraction processes affecting waves are amenable to quantitative description and analysis. Such treatments are applied to a wave passing through one or more slits whose width is specified as a proportion of the wavelength. Numerical approximations may be used, including the Fresnel and Fraunhofer approximations. General diffraction Because diffraction is the result of addition of all waves (of given wavelength) along all unobstructed paths, the usual procedure is to consider the contribution of an infinitesimally small neighborhood around a certain path (this contribution is usually called a wavelet) and then integrate over all paths (= add all wavelets) from the source to the detector (or given point on a screen). Thus in order to determine the pattern produced by diffraction, the phase and the amplitude of each of the wavelets is calculated. That is, at each point in space we must determine the distance to each of the simple sources on the incoming wavefront. If the d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave
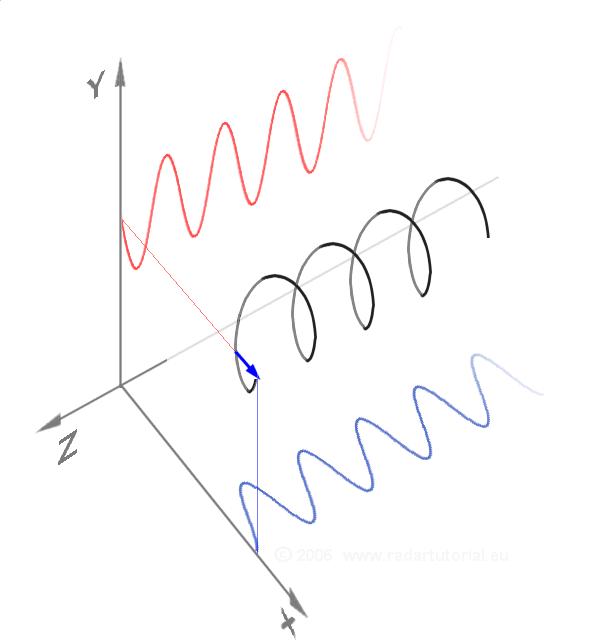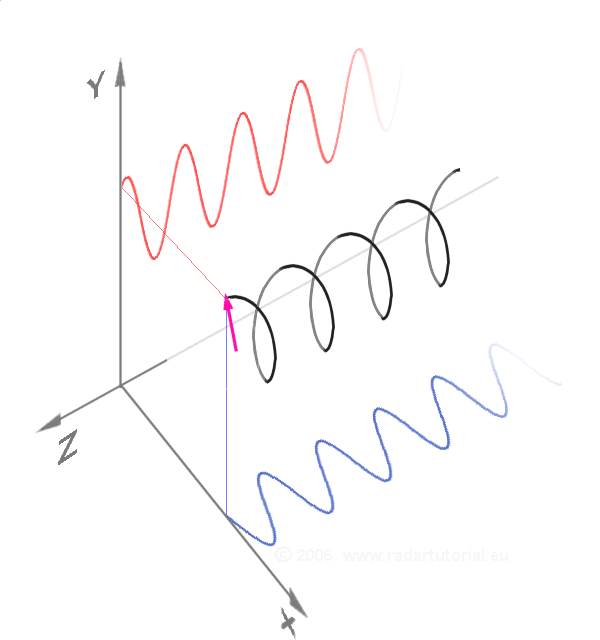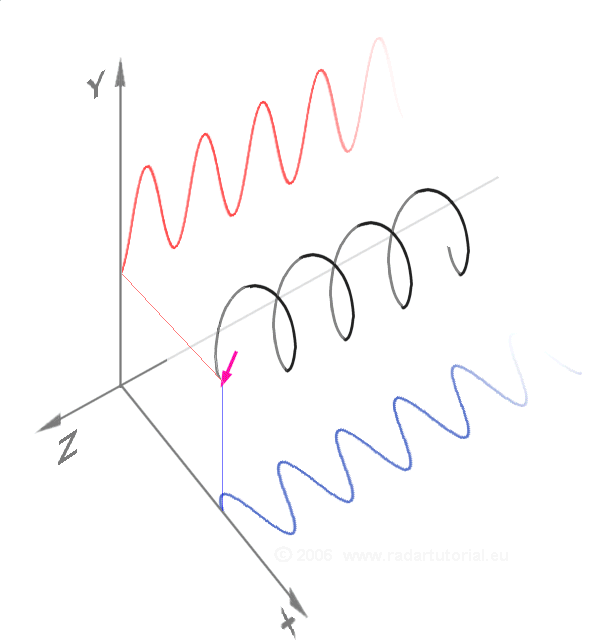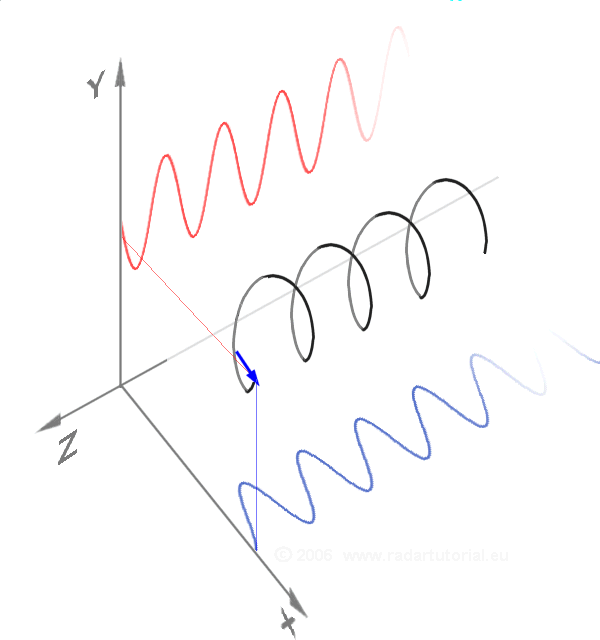
In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance (change from List of types of equilibrium, equilibrium) of one or more quantities. ''Periodic waves'' oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a travelling wave; by contrast, a pair of superposition principle, superimposed periodic waves traveling in opposite directions makes a ''standing wave''. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. There are two types of waves that are most commonly studied in classical physics: mechanical waves and electromagnetic waves. In a mechanical wave, Stress (mechanics), stress and Strain (mechanics), strain fields oscillate about a mechanical equilibrium. A mechanical wave is a local deformation (physics), deformation (strain) in some physical medium that propa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - bi. The complex conjugate of z is often denoted as \overline or z^*. In polar form, if r and \varphi are real numbers then the conjugate of r e^ is r e^. This can be shown using Euler's formula. The product of a complex number and its conjugate is a real number: a^2 + b^2 (or r^2 in polar coordinates). If a root of a univariate polynomial with real coefficients is complex, then its complex conjugate is also a root. Notation The complex conjugate of a complex number z is written as \overline z or z^*. The first notation, a vinculum, avoids confusion with the notation for the conjugate transpose of a matrix, which can be thought of as a generalization of the complex conjugate. The second is preferred in physics, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Envelope (waves)
In physics and engineering, the envelope of an oscillating signal is a smooth curve outlining its extremes. The envelope thus generalizes the concept of a constant amplitude into an instantaneous amplitude. The figure illustrates a modulated sine wave varying between an ''upper envelope'' and a ''lower envelope''. The envelope function may be a function of time, space, angle, or indeed of any variable. In beating waves A common situation resulting in an envelope function in both space ''x'' and time ''t'' is the superposition of two waves of almost the same wavelength and frequency: : \begin F(x, \ t) & = \sin \left[ 2 \pi \left( \frac - ( f + \Delta f )t \right) \right] + \sin \left[ 2 \pi \left( \frac - ( f - \Delta f )t \right) \right] \\[6pt] & \approx 2\cos \left[ 2 \pi \left( \frac - \Delta f \ t \right) \right] \ \sin \left[ 2 \pi \left( \frac - f \ t \right) \right] \end which uses the trigonometric formula for the Trigonometric identity#Product-to-sum an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffraction Grating
In optics, a diffraction grating is an optical grating with a periodic structure that diffraction, diffracts light, or another type of electromagnetic radiation, into several beams traveling in different directions (i.e., different diffraction angles). The emerging coloration is a form of structural coloration. The directions or diffraction angles of these beams depend on the wave (light) Angle of incidence (optics), incident angle to the diffraction grating, the spacing or periodic distance between adjacent diffracting elements (e.g., parallel slits for a transmission grating) on the grating, and the wavelength of the incident light. The grating acts as a dispersion (optics), dispersive element. Because of this, diffraction gratings are commonly used in monochromators and spectrometers, but other applications are also possible such as optical encoders for high-precision motion control and wavefront measurement. For typical applications, a reflection (optics), reflective grati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinc Function
In mathematics, physics and engineering, the sinc function ( ), denoted by , has two forms, normalized and unnormalized.. In mathematics, the historical unnormalized sinc function is defined for by \operatorname(x) = \frac. Alternatively, the unnormalized sinc function is often called the sampling function, indicated as Sa(''x''). In digital signal processing and information theory, the normalized sinc function is commonly defined for by \operatorname(x) = \frac. In either case, the value at is defined to be the limiting value \operatorname(0) := \lim_\frac = 1 for all real (the limit can be proven using the squeeze theorem). The normalization causes the definite integral of the function over the real numbers to equal 1 (whereas the same integral of the unnormalized sinc function has a value of ). As a further useful property, the zeros of the normalized sinc function are the nonzero integer values of . The normalized sinc function is the Fourier transform of the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number , one has e^ = \cos x + i \sin x, where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted ("cosine plus ''i'' sine"). The formula is still valid if is a complex number, and is also called ''Euler's formula'' in this more general case. Euler's formula is ubiquitous in mathematics, physics, chemistry, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics". When , Euler's formula may be rewritten as or , which is known as Euler's identity. History In 1714, the English mathematician Roger Cotes prese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter), psi, respectively). Wave functions are complex number, complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density function, probability density of measurement in quantum mechanics, measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called ''normalization''. Since the wave function is complex-valued, only its relative phase and relative magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Expansion
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, the power expands into a polynomial with terms of the form , where the exponents and are nonnegative integers satisfying and the coefficient of each term is a specific positive integer depending on and . For example, for , (x+y)^4 = x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4. The coefficient in each term is known as the binomial coefficient or (the two have the same value). These coefficients for varying and can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where gives the number of different combinations (i.e. subsets) of elements that can be chosen from an -element set. Therefore is usually pronounced as " choose ". Statement According to the theorem, the expansion of any nonnegative integer power of the binomial is a sum of the form (x+y)^n = x^n y^0 + x^ y^1 + x^ y^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |