|
K2P
A number of different Markov models of DNA sequence evolution have been proposed. These substitution models differ in terms of the parameters used to describe the rates at which one nucleotide replaces another during evolution. These models are frequently used in molecular phylogenetic analyses. In particular, they are used during the calculation of likelihood of a tree (in Bayesian and maximum likelihood approaches to tree estimation) and they are used to estimate the evolutionary distance between sequences from the observed differences between the sequences. Introduction These models are phenomenological descriptions of the evolution of DNA as a string of four discrete states. These Markov models do not explicitly depict the mechanism of mutation nor the action of natural selection. Rather they describe the relative rates of different changes. For example, mutational biases and purifying selection favoring conservative changes are probably both responsible for the relatively ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Substitution Model
In biology, a substitution model, also called models of DNA sequence evolution, are Markov models that describe changes over evolutionary time. These models describe evolutionary changes in macromolecules (e.g., DNA sequences) represented as sequence of symbols (A, C, G, and T in the case of DNA). Substitution models are used to calculate the likelihood of phylogenetic trees using multiple sequence alignment data. Thus, substitution models are central to maximum likelihood estimation of phylogeny as well as Bayesian inference in phylogeny. Estimates of evolutionary distances (numbers of substitutions that have occurred since a pair of sequences diverged from a common ancestor) are typically calculated using substitution models (evolutionary distances are used input for distance methods such as neighbor joining). Substitution models are also central to phylogenetic invariants because they are necessary to predict site pattern frequencies given a tree topology. Substitution mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homoplasy
Homoplasy, in biology and phylogenetics, is the term used to describe a feature that has been gained or lost independently in separate lineages over the course of evolution. This is different from homology, which is the term used to characterize the similarity of features that can be parsimoniously explained by common ancestry. Homoplasy can arise from both similar selection pressures acting on adapting species, and the effects of genetic drift. Most often, homoplasy is viewed as a similarity in morphological characters. However, homoplasy may also appear in other character types, such as similarity in the genetic sequence, life cycle types or even behavioral traits. Etymology The term homoplasy was first used by Ray Lankester in 1870. The corresponding adjective is either ''homoplasic'' or ''homoplastic''. It is derived from the two Ancient Greek words (), meaning "similar, alike, the same", and (), meaning "to shape, to mold". Parallelism and convergence Parallel a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-reversibility
A mathematical or physical process is time-reversible if the dynamics of the process remain well-defined when the sequence of time-states is reversed. A deterministic process is time-reversible if the time-reversed process satisfies the same dynamic equations as the original process; in other words, the equations are invariant or symmetrical under a change in the sign of time. A stochastic process is reversible if the statistical properties of the process are the same as the statistical properties for time-reversed data from the same process. Mathematics In mathematics, a dynamical system is time-reversible if the forward evolution is one-to-one, so that for every state there exists a transformation (an involution) π which gives a one-to-one mapping between the time-reversed evolution of any one state and the forward-time evolution of another corresponding state, given by the operator equation: :U_ = \pi \, U_\, \pi Any time-independent structures (e.g. critical points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas H
Thomas may refer to: People * List of people with given name Thomas * Thomas (name) * Thomas (surname) * Saint Thomas (other) * Thomas Aquinas (1225–1274) Italian Dominican friar, philosopher, and Doctor of the Church * Thomas the Apostle * Thomas (bishop of the East Angles) (fl. 640s–650s), medieval Bishop of the East Angles * Thomas (Archdeacon of Barnstaple) (fl. 1203), Archdeacon of Barnstaple * Thomas, Count of Perche (1195–1217), Count of Perche * Thomas (bishop of Finland) (1248), first known Bishop of Finland * Thomas, Earl of Mar (1330–1377), 14th-century Earl, Aberdeen, Scotland Geography Places in the United States * Thomas, Illinois * Thomas, Indiana * Thomas, Oklahoma * Thomas, Oregon * Thomas, South Dakota * Thomas, Virginia * Thomas, Washington * Thomas, West Virginia * Thomas County (other) * Thomas Township (other) Elsewhere * Thomas Glacier (Greenland) Arts, entertainment, and media * ''Thomas'' (Burton ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles Cantor
Charles R. Cantor (born 26 August 1942) is an American molecular geneticist who, in conjunction with David Schwartz, developed pulse field gel electrophoresis for very large DNA molecules. Cantor's three-volume book, ''Biophysical Chemistry'' co-authored with Paul Schimmel, was an influential textbook in the 1980s and 1990s. Career Charles Cantor received his AB from Columbia University in 1963 and PhD from University of California, Berkeley in 1966. He is Director of the Center for Advanced Biotechnology at Boston University. While on a two-year sabbatical acting as Chief Scientific Officer at Sequenom, Inc. he maintained his research laboratory at Boston University. He is also a co-founder and Director of Retrotope, a US-based company using heavier isotopes of carbon (13C) and hydrogen (2H, deuterium) to stabilize essential compounds like amino acids, nucleic acids and lipids to target age-related diseases. Cantor held positions at Columbia University (1981–1989) an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
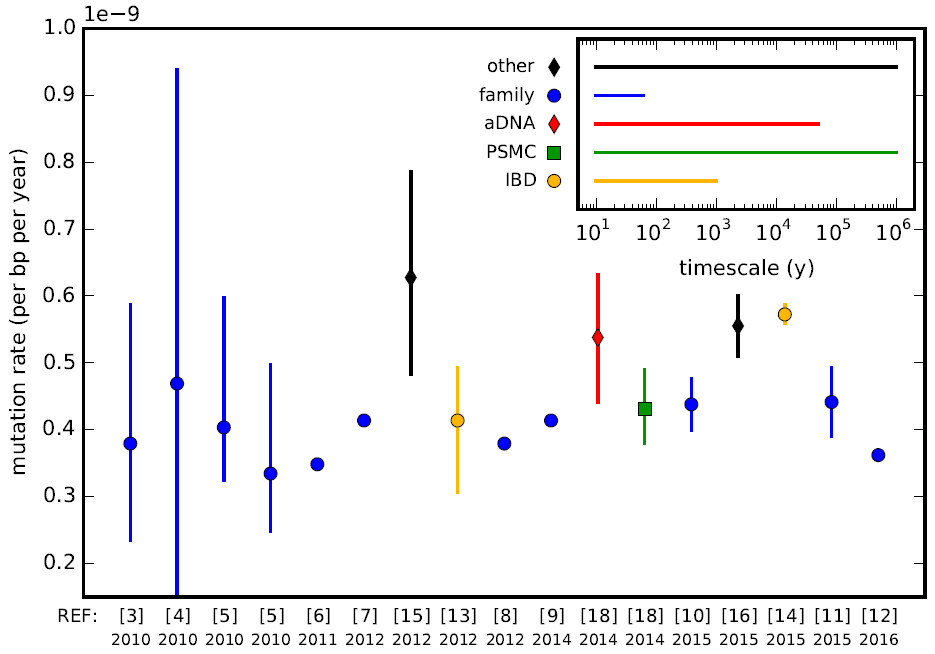
Mutation Rates
In genetics, the mutation rate is the frequency of new mutations in a single gene or organism over time. Mutation rates are not constant and are not limited to a single type of mutation; there are many different types of mutations. Mutation rates are given for specific classes of mutations. Point mutations are a class of mutations which are changes to a single base. Missense and Nonsense mutations are two subtypes of point mutations. The rate of these types of substitutions can be further subdivided into a mutation spectrum which describes the influence of the genetic context on the mutation rate. There are several natural units of time for each of these rates, with rates being characterized either as mutations per base pair per cell division, per gene per generation, or per genome per generation. The mutation rate of an organism is an evolved characteristic and is strongly influenced by the genetics of each organism, in addition to strong influence from the environment. The upper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamming Distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of ''substitutions'' required to change one string into the other, or the minimum number of ''errors'' that could have transformed one string into the other. In a more general context, the Hamming distance is one of several string metrics for measuring the edit distance between two sequences. It is named after the American mathematician Richard Hamming. A major application is in coding theory, more specifically to block codes, in which the equal-length strings are vectors over a finite field. Definition The Hamming distance between two equal-length strings of symbols is the number of positions at which the corresponding symbols are different. Examples The symbols may be letters, bits, or decimal digits, among other possibilities. For example, the Hamming distance betwe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sufficient Statistic
In statistics, a statistic is ''sufficient'' with respect to a statistical model and its associated unknown parameter if "no other statistic that can be calculated from the same sample provides any additional information as to the value of the parameter". In particular, a statistic is sufficient for a family of probability distributions if the sample from which it is calculated gives no additional information than the statistic, as to which of those probability distributions is the sampling distribution. A related concept is that of linear sufficiency, which is weaker than ''sufficiency'' but can be applied in some cases where there is no sufficient statistic, although it is restricted to linear estimators. The Kolmogorov structure function deals with individual finite data; the related notion there is the algorithmic sufficient statistic. The concept is due to Sir Ronald Fisher in 1920. Stephen Stigler noted in 1973 that the concept of sufficiency had fallen out of favor in des ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Motoo Kimura
(November 13, 1924 – November 13, 1994) was a Japanese biologist best known for introducing the neutral theory of molecular evolution in 1968. He became one of the most influential theoretical population geneticists. He is remembered in genetics for his innovative use of diffusion equations to calculate the probability of fixation of beneficial, deleterious, or neutral alleles. Combining theoretical population genetics with molecular evolution data, he also developed the neutral theory of molecular evolution in which genetic drift is the main force changing allele frequencies. James F. Crow, himself a renowned population geneticist, considered Kimura to be one of the two greatest evolutionary geneticists, along with Gustave Malécot, after the great trio of the modern synthesis, Ronald Fisher, J. B. S. Haldane, and Sewall Wright. Life and work Kimura was born in Okazaki, Aichi Prefecture. From an early age he was very interested in botany, though he also excelled at ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
_JC69_Pij_Pii.jpg)