|
J.J. Sylvester
James Joseph Sylvester (3 September 1814 – 15 March 1897) was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory, and combinatorics. He played a leadership role in American mathematics in the later half of the 19th century as a professor at the Johns Hopkins University and as founder of the ''American Journal of Mathematics''. At his death, he was a professor at Oxford University. Biography James Joseph was born in London on 3 September 1814, the son of Abraham Joseph, a Jewish merchant. James later adopted the surname ''Sylvester'' when his older brother did so upon emigration to the United States. At the age of 14, Sylvester was a student of Augustus De Morgan at the University of London (now University College London). His family withdrew him from the university after he was accused of stabbing a fellow student with a knife. Subsequently, he attended the Liverpool Royal Institution. Sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Professor
Professor (commonly abbreviated as Prof.) is an Academy, academic rank at university, universities and other tertiary education, post-secondary education and research institutions in most countries. Literally, ''professor'' derives from Latin as a 'person who professes'. Professors are usually experts in their field and teachers of the highest rank. In most systems of List of academic ranks, academic ranks, "professor" as an unqualified title refers only to the most senior academic position, sometimes informally known as "full professor". In some countries and institutions, the word ''professor'' is also used in titles of lower ranks such as associate professor and assistant professor; this is particularly the case in the United States, where the unqualified word is also used colloquially to refer to associate and assistant professors as well, and often to instructors or lecturers. Professors often conduct original research and commonly teach undergraduate, Postgraduate educa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Roberts McDaniel
William Roberts McDaniel (August 11, 1861 – April 19, 1942) is the namesake for McDaniel College in Westminster, Maryland. Biography William Roberts McDaniel was born in Talbot County, Maryland. He was the youngest child of a non-traditional family having two brothers, five sisters, two half-brothers, and two half-sisters. His father, John Wesley Sedgewick McDaniel, was first married to Sarah Wrightson before marrying her sister, Ann. It was Ann who later gave birth to William and his siblings. When he was just sixteen and a sophomore, McDaniel matriculated into Western Maryland College. Upon graduation in 1880, McDaniel earned the position of salutatorian of his class. McDaniel was an active member of the College's Alumni Association and received recognition for his outstanding service to his alma mater. Interrupting his doctorate from Johns Hopkins University and his studies with world-renowned British mathematician James Joseph Sylvester in 1885, he returned to school as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester's Triangle Problem
Sylvester's theorem or Sylvester's formula describes a particular interpretation of the sum of three pairwise distinct vector (mathematics and physics), vectors of equal length in the context of triangle geometry. It is also referred to as Sylvester's (triangle) problem in literature, when it is given as a problem rather than a theorem. The theorem is named after the British mathematician James Joseph Sylvester. Theorem Consider three pairwise distinct vectors of equal length \vec, \vec and \vec each of them acting on the same point O thus creating the points A, B and C. Those points form the triangle \triangle ABC with O as the center of its circumcircle. Now let H denote the orthocenter of the triangle, then connection vector \overrightarrow is equal to the sum of the three vectors: :\overrightarrow=\vec+\vec+\vec Furthermore, since the points O and H are located on the Euler line together with the centroid S the following equation holds:Michael de Villiers: "'Generalising a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester's Law Of Inertia
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of basis. Namely, if A is a symmetric matrix, then for any invertible matrix S, the number of positive, negative and zero eigenvalues (called the inertia of the matrix) of D=SAS^\mathrm is constant. This result is particularly useful when D is diagonal, as the inertia of a diagonal matrix can easily be obtained by looking at the sign of its diagonal elements. This property is named after James Joseph Sylvester who published its proof in 1852. Statement Let A be a symmetric square matrix of order n with real entries. Any non-singular matrix S of the same size is said to transform A into another symmetric matrix , also of order , where S^\mathrm is the transpose of . It is also said that matrices A and B are congruent. If A is the coefficient matrix of some quadratic form of , then B is the matrix fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester–Gallai Theorem
The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944. A line that contains exactly two of a set of points is known as an ''ordinary line''. Another way of stating the theorem is that every finite set of points that is not collinear has an ordinary line. According to a strengthening of the theorem, every finite point set (not all on one line) has at least a linear number of ordinary lines. An algorithm can find an ordinary line in a set of n points in time O(n\log n). History The Sylvester–Gallai theorem was posed as a problem by . suggests that Sylvester may have been motivated by a related phenomenon in algebraic geometry, in which the inflection points of a cubic curve i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester Matrix
In mathematics, a Sylvester matrix is a matrix associated to two univariate polynomials with coefficients in a field or a commutative ring. The entries of the Sylvester matrix of two polynomials are coefficients of the polynomials. The determinant of the Sylvester matrix of two polynomials is their resultant, which is zero when the two polynomials have a common root (in case of coefficients in a field) or a non-constant common divisor (in case of coefficients in an integral domain). Sylvester matrices are named after James Joseph Sylvester. Definition Formally, let ''p'' and ''q'' be two nonzero polynomials, respectively of degree ''m'' and ''n''. Thus: :p(z)=p_0+p_1 z+p_2 z^2+\cdots+p_m z^m,\;q(z)=q_0+q_1 z+q_2 z^2+\cdots+q_n z^n. The Sylvester matrix associated to ''p'' and ''q'' is then the (n+m)\times(n+m) matrix constructed as follows: * if ''n'' > 0, the first row is: :\begin p_m & p_ & \cdots & p_1 & p_0 & 0 & \cdots & 0 \end. * the second row is the first row, shifted on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester's Formula
In matrix theory, Sylvester's formula or Sylvester's matrix theorem (named after J. J. Sylvester) or Lagrange−Sylvester interpolation expresses an analytic function of a matrix as a polynomial in , in terms of the eigenvalues and eigenvectors of ./ Roger A. Horn and Charles R. Johnson (1991), ''Topics in Matrix Analysis''. Cambridge University Press, Jon F. Claerbout (1976), ''Sylvester's matrix theorem'', a section of ''Fundamentals of Geophysical Data Processing''Online versionat sepwww.stanford.edu, accessed on 2010-03-14. It states that : f(A) = \sum_^k f(\lambda_i) ~A_i ~, where the are the eigenvalues of , and the matrices : A_i \equiv \prod_^k \frac \left(A - \lambda_j I\right) are the corresponding Frobenius covariants of , which are (projection) matrix Lagrange polynomials of . Conditions Sylvester's formula applies for any diagonalizable matrix with distinct eigenvalues, 1, ..., ''k'', and any function defined on some subset of the complex nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvester's Sequence
In number theory, Sylvester's sequence is an integer sequence in which each term is the product of the previous terms, plus one. Its first few terms are :2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443 . Sylvester's sequence is named after James Joseph Sylvester, who first investigated it in 1880. Its values grow doubly exponentially, and the sum of its reciprocals forms a series of unit fractions that converges to 1 more rapidly than any other series of unit fractions. The recurrence by which it is defined allows the numbers in the sequence to be factored more easily than other numbers of the same magnitude, but, due to the rapid growth of the sequence, complete prime factorizations are known only for a few of its terms. Values derived from this sequence have also been used to construct finite Egyptian fraction representations of 1, Sasakian Einstein manifolds, and hard instances for online algorithms. Formal definitions Formally, Sylv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
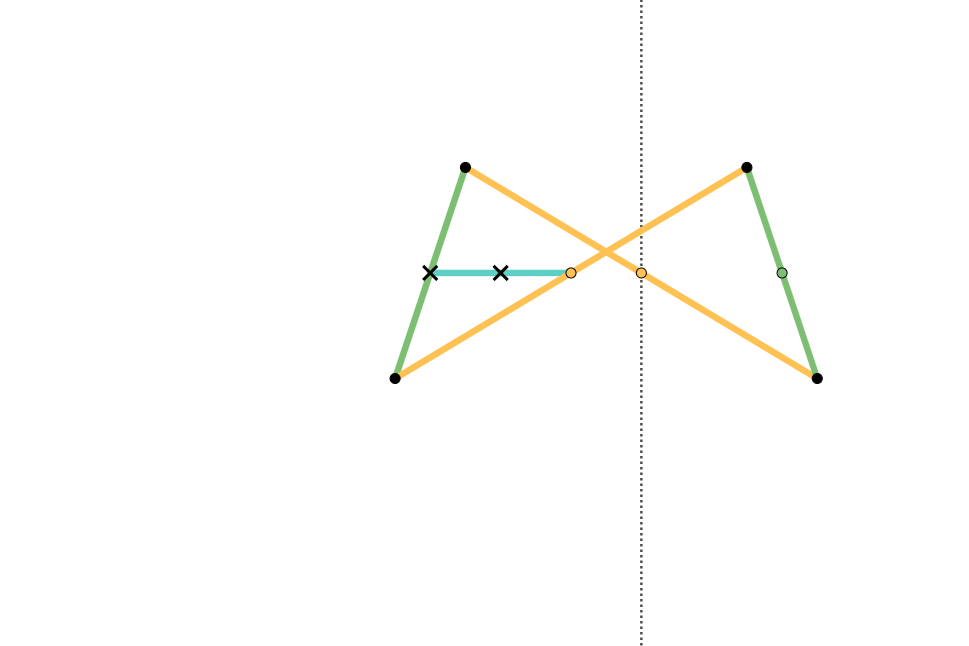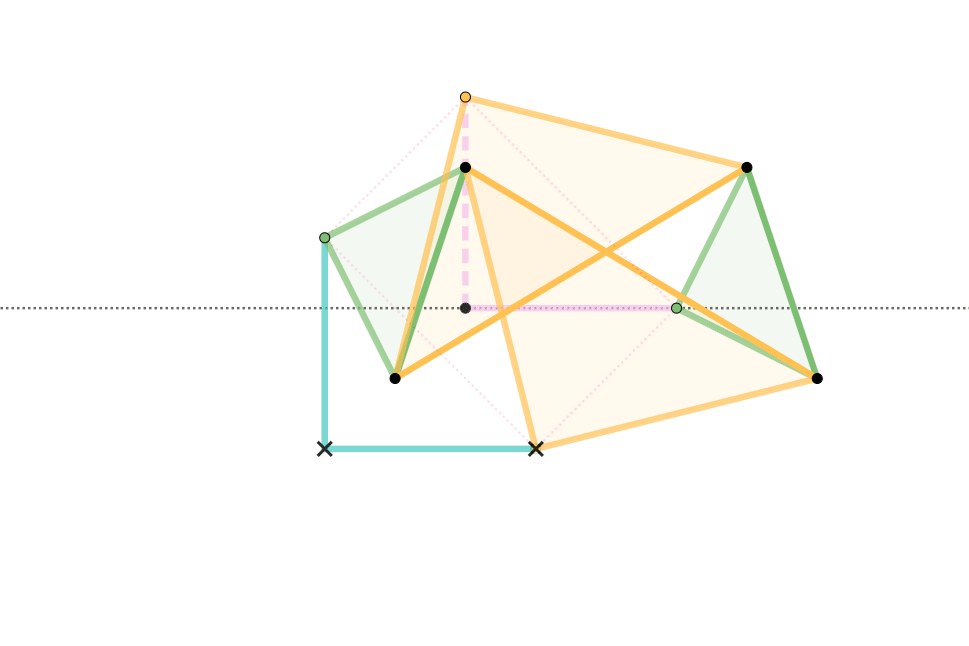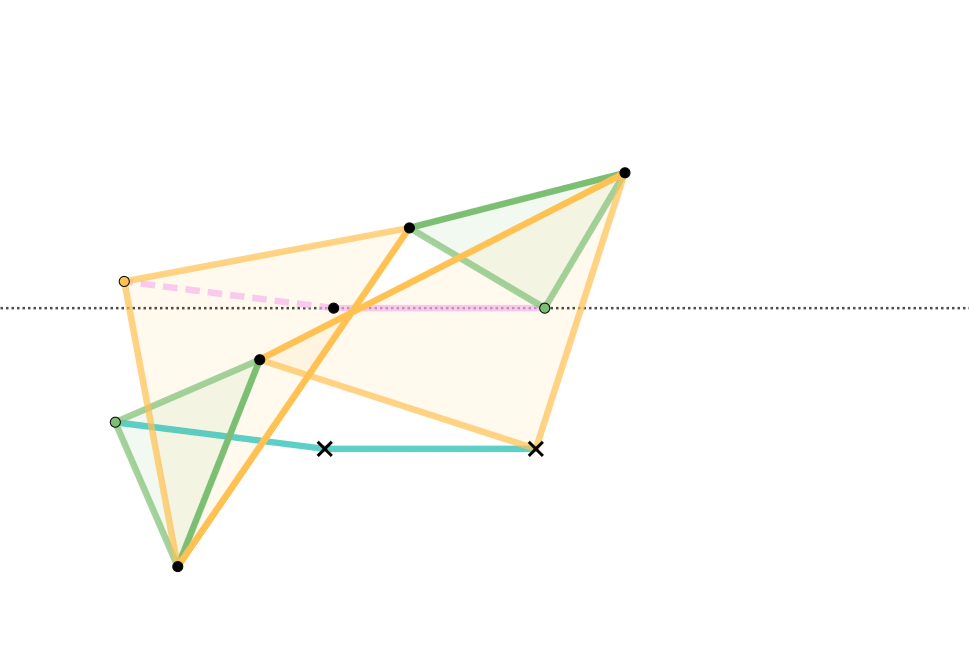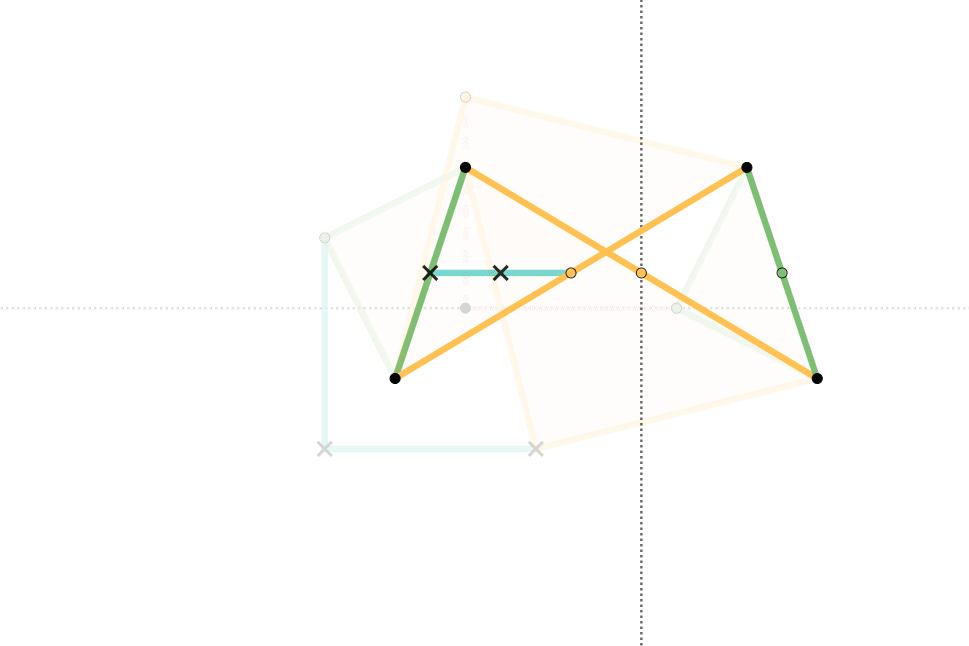
Quadruplanar Inversor
The Quadruplanar inversor of Sylvester and Kempe is a generalization of Hart's inversor. Like Hart's inversor, is a mechanism that provides a perfect straight line motion without sliding guides. The mechanism was described in 1875 by James Joseph Sylvester in the journal Nature (journal), Nature. Like Hart's inversor, it is based on an antiparallelogram but the rather than placing the fixed, input and output points on the sides (dividing them in fixed proportion so they are all similar), Sylvester recognized that the additional points could be displaced sideways off the sides, as long as they formed similar triangles. Hart's original form is simply the degenerate case of triangles with altitude zero. Gallery In these diagrams: * The antiparallelogram is highlighted in full opacity links. * Yellow Triangles and Green Triangles are similar. ** Green Triangles are congruent with each other. ** Yellow Triangles are congruent with each other. * Cyan links and Pink links are congruen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number Theorem
In mathematics, the prime number theorem (PNT) describes the asymptotic analysis, asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann (in particular, the Riemann zeta function). The first such distribution found is , where is the prime-counting function (the number of primes less than or equal to ''N'') and is the natural logarithm of . This means that for large enough , the probability that a random integer not greater than is prime is very close to . Consequently, a random integer with at most digits (for large enough ) is about half as likely to be prime as a random integer with at most digits. For example, among the positive integers of at most 1000 digits, about on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the zero of a function, roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factorization, polynomial factoring, number theory, and algebraic geometry. The discriminant of the quadratic polynomial ax^2+bx+c is :b^2-4ac, the quantity which appears under the square root in the quadratic formula. If a\ne 0, this discriminant is zero if and only if the polynomial has a double root. In the case of real number, real coefficients, it is positive if the polynomial has two distinct real roots, and negative if it has two distinct complex conjugate roots. Similarly, the discriminant of a cubic polynomial is zero if and only if the polynomial has a multiple root. In the case of a cubic with real coefficients, the discriminant is positive if the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |