|
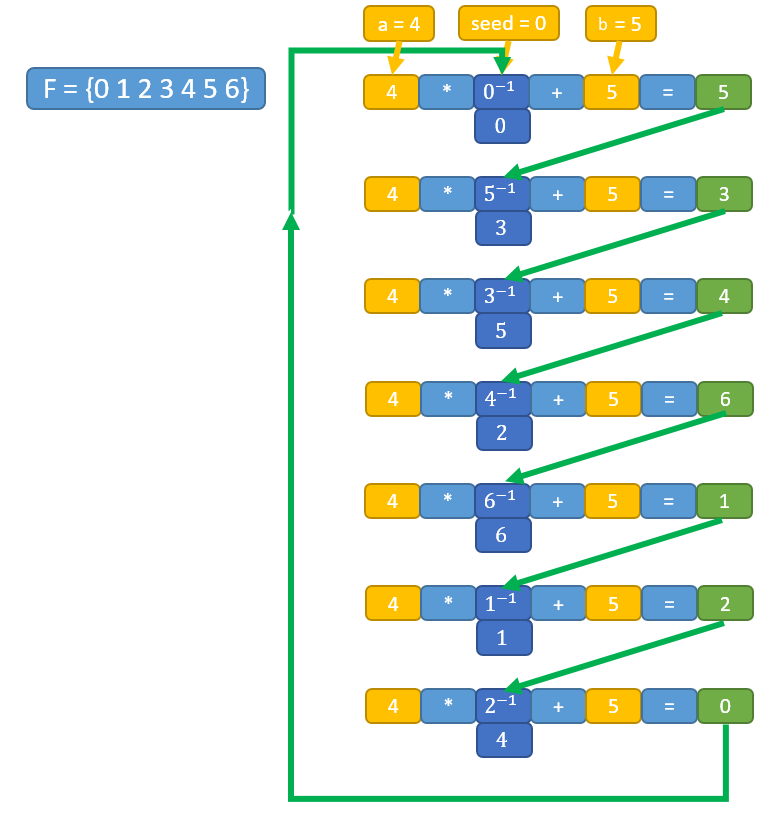
Inversive Congruential Generator
Inversive congruential generators are a type of nonlinear congruential pseudorandom number generator, which use the modular multiplicative inverse (if it exists) to generate the next number in a sequence. The standard formula for an inversive congruential generator, modulo some prime ''q'' is: : x_0 = \text, : x_ = \begin (ax_i^ + c) \bmod q & \text x_i \ne 0, \\ c & \text x_i = 0. \end Such a generator is denoted symbolically as and is said to be an ICG with parameters ''q'', ''a'', ''c'' and seed ''seed''. Period The sequence (x_n)_ must have x_i = x_j after finitely many steps, and since the next element depends only on its direct predecessor, also x_ = x_ etc. The maximum possible period for the modulus ''q'' is ''q'' itself, i.e. the sequence includes every value from 0 to ''q'' − 1 before repeating. A sufficient condition for the sequence to have the maximum possible period is to choose ''a'' and ''c'' such that the polynomial f(x) = x^2 - cx - a \in \mathbb F_q /math> ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables in a probability space, where the index of the family often has the interpretation of time. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology Ecology () is the natural science of the relationships among living organisms and their Natural environment, environment. Ecology considers organisms at the individual, population, community (ecology), community, ecosystem, and biosphere lev ..., neuroscience, physics, image processing, signal processing, stochastic control, control theory, information theory, computer scien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Inversive Congruential Pseudorandom Numbers
An approach to nonlinear congruential methods of generating uniform pseudorandom numbers in the interval primes p_1,\dots ,p_r \ge 5 will be present here. Let \mathbb_ = \ . For integers a,b \in \mathbb_ with gcd (a,m) = 1 a generalized inversive congruential sequence (y_)_ of elements of \mathbb_ is defined by : y_ = : y_\equiv a y_^ + b \pmod m \textn \geqslant 0 where \varphi(m)=(p_-1)\dots (p_-1) denotes the number of positive integers less than ''m'' which are relatively prime In number theory, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equiv ... to ''m''. Example Let take m = 15 = 3 \times 5\, a=2 , b=3 and y_0= 1. Hence \varphi (m)= 2 \times 4=8 \, and the sequence (y_)_=(1,5,13,2,4,7,1,\dots ) is not maximum. The result below shows that these sequences are closely re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Congruential Generator
A linear congruential generator (LCG) is an algorithm that yields a sequence of pseudo-randomized numbers calculated with a discontinuous piecewise linear equation. The method represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is relatively easy to understand, and they are easily implemented and fast, especially on computer hardware which can provide modular arithmetic by storage-bit truncation. The generator is defined by the recurrence relation: :X_ = \left( a X_n + c \right)\bmod m where X is the sequence of pseudo-random values, and : m,\, 0 |
List Of Random Number Generators
Random number generators are important in many kinds of technical applications, including physics, engineering or mathematical computer studies (e.g., Monte Carlo simulations), cryptography and gambling (on game servers). This list includes many common types, regardless of quality or applicability to a given use case. Pseudorandom number generators (PRNGs) The following algorithms are pseudorandom number generators. Cryptographic algorithms Cipher algorithms and cryptographic hashes can be used as very high-quality pseudorandom number generators. However, generally they are considerably slower (typically by a factor 2–10) than fast, non-cryptographic random number generators. These include: * Stream ciphers. Popular choices are Salsa20 or ChaCha (often with the number of rounds reduced to 8 for speed), ISAAC, HC-128 and RC4. * Block ciphers in counter mode. Common choices are AES (which is very fast on systems supporting it in hardware), TwoFish, Serpent and Camel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudorandom Number Generator
A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG), is an algorithm for generating a sequence of numbers whose properties approximate the properties of sequences of random number generation, random numbers. The PRNG-generated sequence is not truly random, because it is completely determined by an initial value, called the PRNG's ''random seed, seed'' (which may include truly random values). Although sequences that are closer to truly random can be generated using hardware random number generators, ''pseudorandom number generators'' are important in practice for their speed in number generation and their reproducibility. PRNGs are central in applications such as simulations (e.g. for the Monte Carlo method), electronic games (e.g. for procedural generation), and cryptography. Cryptographic applications require the output not to be predictable from earlier outputs, and more cryptographically-secure pseudorandom number generator, elabora ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cryptography
Cryptography, or cryptology (from "hidden, secret"; and ''graphein'', "to write", or ''-logy, -logia'', "study", respectively), is the practice and study of techniques for secure communication in the presence of Adversary (cryptography), adversarial behavior. More generally, cryptography is about constructing and analyzing Communication protocol, protocols that prevent third parties or the public from reading private messages. Modern cryptography exists at the intersection of the disciplines of mathematics, computer science, information security, electrical engineering, digital signal processing, physics, and others. Core concepts related to information security (confidentiality, data confidentiality, data integrity, authentication, and non-repudiation) are also central to cryptography. Practical applications of cryptography include electronic commerce, Smart card#EMV, chip-based payment cards, digital currencies, password, computer passwords, and military communications. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primitive Element (finite Field)
In field theory, a primitive element of a finite field is a generator of the multiplicative group of the field. In other words, is called a primitive element if it is a primitive th root of unity in ; this means that each non-zero element of can be written as for some natural number . If is a prime number, the elements of can be identified with the integers modulo . In this case, a primitive element is also called a primitive root modulo . For example, 2 is a primitive element of the field and , but not of since it generates the cyclic subgroup of order 3; however, 3 is a primitive element of . The minimal polynomial of a primitive element is a primitive polynomial. Properties Number of primitive elements The number of primitive elements in a finite field is , where is Euler's totient function, which counts the number of elements less than or equal to that are coprime In number theory, two integers and are coprime, relatively prime or mutually prime i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudorandom Number Generator
A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG), is an algorithm for generating a sequence of numbers whose properties approximate the properties of sequences of random number generation, random numbers. The PRNG-generated sequence is not truly random, because it is completely determined by an initial value, called the PRNG's ''random seed, seed'' (which may include truly random values). Although sequences that are closer to truly random can be generated using hardware random number generators, ''pseudorandom number generators'' are important in practice for their speed in number generation and their reproducibility. PRNGs are central in applications such as simulations (e.g. for the Monte Carlo method), electronic games (e.g. for procedural generation), and cryptography. Cryptographic applications require the output not to be predictable from earlier outputs, and more cryptographically-secure pseudorandom number generator, elabora ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harald Niederreiter
Harald G. Niederreiter (born June 7, 1944) is an Austrian mathematician known for his work in discrepancy theory, algebraic geometry, quasi-Monte Carlo methods, and cryptography. Education and career Niederreiter was born on June 7, 1944, in Vienna, and grew up in Salzburg... He began studying mathematics at the University of Vienna in 1963, and finished his doctorate there in 1969, with a thesis on discrepancy in compact abelian groups supervised by Edmund Hlawka. He began his academic career as an assistant professor at the University of Vienna, but soon moved to Southern Illinois University. During this period he also visited the University of Illinois at Urbana-Champaign, Institute for Advanced Study, and University of California, Los Angeles. In 1978 he moved again, becoming the head of a new mathematics department at the University of the West Indies in Jamaica. In 1981 he returned to Austria for a post at the Austrian Academy of Sciences, where from 1989 to 2000 he serve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |