|
Hu–Washizu Principle
In continuum mechanics, and in particular in finite element analysis, the Hu–Washizu principle is a variational principle which says that the action :\int_ \left \frac \varepsilon^T C \varepsilon - \sigma^T \varepsilon + \sigma^T (\nabla u) - \bar^T u \rightdV - \int_ \bar^T u\ dS is stationary, where C is the elastic stiffness tensor. The Hu–Washizu principle is used to develop mixed finite element methods. The principle is named after Hu Haichang and Kyūichirō Washizu Kyūichirō Washizu (鷲津 久一郎, ''Washizu Kyūichirō''; March 12, 1921 – November 25, 1981) was a Japanese aircraft engineer and academic. He served as professor of aeronautical engineering at the University of Tokyo and professor of eng .... References Further reading * K. Washizu: ''Variational Methods in Elasticity & Plasticity'', Pergamon Press, New York, 3rd edition (1982) * O. C. Zienkiewicz, R. L. Taylor, J. Z. Zhu : ''The Finite Element Method: Its Basis and Fundamentals'', Butterwort ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century. Explanation A continuum model assumes that the substance of the object fills the space it occupies. Modeling objects in this way ignores the fact that matter is made of atoms, and so is not continuous; however, on length scales much greater than that of inter-atomic distances, such models are highly accurate. These models can be used to derive differential equations that describe the behavior of such objects using physical laws, such as mass conservation, momentum conservation, and energy conservation, and some information about the material is provided by constitutive relationships. Continuum mechanics deals with the physical properties of solids and fluids which are independent of any particular coordinate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
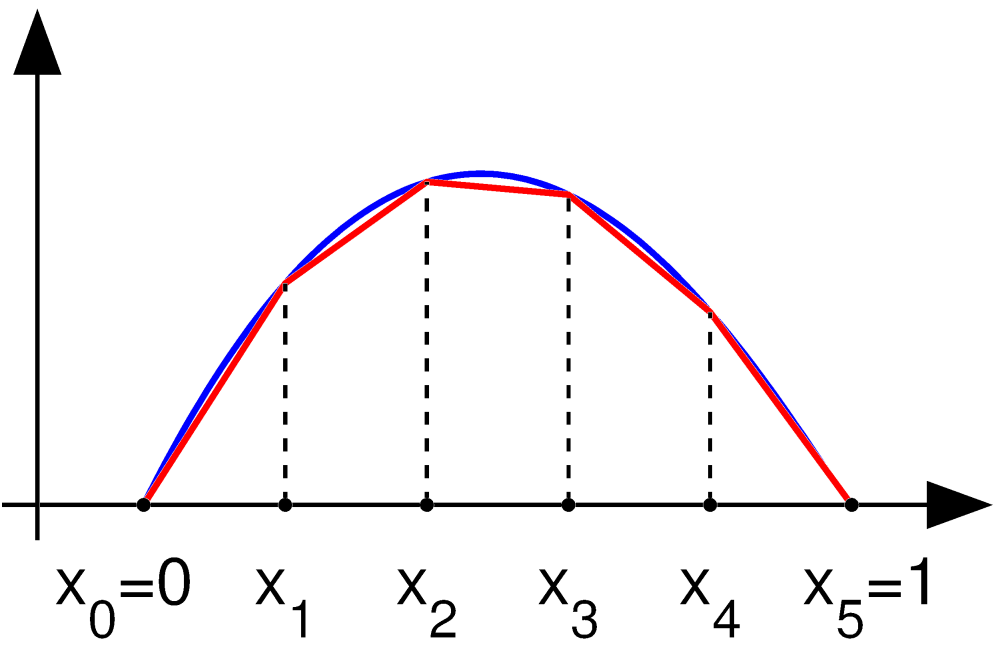
Finite Element Analysis
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The FEM is a general numerical method for solving partial differential equations in two or three space variables (i.e., some boundary value problems). To solve a problem, the FEM subdivides a large system into smaller, simpler parts that are called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approximates the unknown function over the domain. The simple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Principle
In science and especially in mathematical studies, a variational principle is one that enables a problem to be solved using calculus of variations, which concerns finding functions that optimize the values of quantities that depend on those functions. For example, the problem of determining the shape of a hanging chain suspended at both ends—a catenary—can be solved using variational calculus, and in this case, the variational principle is the following: The solution is a function that minimizes the gravitational potential energy of the chain. Overview Any physical law which can be expressed as a variational principle describes a self-adjoint operator. These expressions are also called Hermitian. Such an expression describes an invariant under a Hermitian transformation. History Felix Klein's Erlangen program attempted to identify such invariants under a group of transformations. In what is referred to in physics as Noether's theorem, the Poincaré group of transformations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stiffness Tensor
Stiffness is the extent to which an object resists deformation in response to an applied force. The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is. Calculations The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (DOF) (for example, stretching or compression of a rod), the stiffness is defined as k = \frac where, * F is the force on the body * \delta is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) In the International System of Units, stiffness is typically measured in newtons per meter (N/m). In Imperial units, stiffness is typically measured in pounds (lbs) per inch. Generally speaking, deflections (or motions) of an infinitesimal element (which is viewed as a point) in an elastic body can occur along multiple DOF (maximum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Element Method
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The FEM is a general numerical method for solving partial differential equations in two or three space variables (i.e., some boundary value problems). To solve a problem, the FEM subdivides a large system into smaller, simpler parts that are called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approximates the unknown function over the domain. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hu Haichang
Hu Haichang (; April 25, 1928 – February 21, 2011) was a Chinese mechanical and aerospace engineer. He was in charge of the early phase development for the Dong Fang Hong I, China's first artificial satellite. Hu was an academician of the Chinese Academy of Sciences. Biography Hu was born in Hangzhou, Zhejiang Province in April 1928. Hu graduated from the Department of Civil Engineering, Zhejiang University in Hangzhou, and his academic advisor was Chien Wei-zang. After graduation, Hu joined the Institute of Mechanics of the Chinese Academy of Sciences (CAS) in Beijing, which was mainly founded by Tsien Hsue-shen in 1950s. From 1968 until retired, Hu worked for the CAS Department of Spacecraft System Design. Hu mainly generalized some versatile variational principles especially in elastic mechanics and promoted their corresponding applications such as in the spacecraft system design. Hu worked for China's spacecraft system design as early as 1966. Hu was in charge of the g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kyūichirō Washizu
Kyūichirō Washizu (鷲津 久一郎, ''Washizu Kyūichirō''; March 12, 1921 – November 25, 1981) was a Japanese aircraft engineer and academic. He served as professor of aeronautical engineering at the University of Tokyo and professor of engineering science at the Osaka University. He led the performance-related design of the '' kamikaze'' attack aircraft Yokosuka MXY-7 ''Ohka'' during World War II. Life Washizu was born in Aichi Prefecture on March 12, 1921. After graduating from Ichinomiya High School, he entered the Tokyo Imperial University, Faculty of Engineering. In 1957, he obtained PhD. in Engineering with his thesis "''Study on approximate solution methods in elastic mechanics''". As Captain Technical, Washizu took part in the design of the attack aircraft Yokosuka MXY-7 ''Ohka'' during World War II. He was in charge of performance-related design of the aircraft, and worked alongside Lieutenant Colonel Technical Masao Yamana, as design director; Toshikazu Ki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus Of Variations
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as '' geodesics''. A related problem is posed by Fermat's principle: light follows the path of shortest optical length connecting two points, which depends ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Element Method
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The FEM is a general numerical method for solving partial differential equations in two or three space variables (i.e., some boundary value problems). To solve a problem, the FEM subdivides a large system into smaller, simpler parts that are called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approximates the unknown function over the domain. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Analysis
Structural analysis is a branch of Solid Mechanics which uses simplified models for solids like bars, beams and shells for engineering decision making. Its main objective is to determine the effect of loads on the physical structures and their components. In contrast to theory of elasticity, the models used in structure analysis are often differential equations in one spatial variable. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, aircraft and ships. Structural analysis uses ideas from applied mechanics, materials science and applied mathematics to compute a structure's deformations, internal forces, stresses, support reactions, velocity, accelerations, and stability. The results of the analysis are used to verify a structure's fitness for use, often precluding physical tests. Structural analysis is thus a key part of the engineering design of structures. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principles
A principle is a proposition or value that is a guide for behavior or evaluation. In law, it is a rule that has to be or usually is to be followed. It can be desirably followed, or it can be an inevitable consequence of something, such as the laws observed in nature or the way that a system is constructed. The principles of such a system are understood by its users as the essential characteristics of the system, or reflecting system's designed purpose, and the effective operation or use of which would be impossible if any one of the principles was to be ignored. A system may be explicitly based on and implemented from a document of principles as was done in IBM's 360/370 ''Principles of Operation''. Examples of principles are, entropy in a number of fields, least action in physics, those in descriptive comprehensive and fundamental law: doctrines or assumptions forming normative rules of conduct, separation of church and state in statecraft, the central dogma of molecular biolog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |