|
Hurwitz
Hurwitz is one of the variants of a surname of Ashkenazi Jewish origin (for historical background see the Horowitz page). Notable people with the surname include: *Adolf Hurwitz (1859–1919), German mathematician **Hurwitz polynomial **Hurwitz matrix **Hurwitz quaternion **Hurwitz's automorphisms theorem **Hurwitz zeta function **Hurwitz's theorem (other) Five theorems named after Adolf Hurwitz **Routh–Hurwitz stability criterion * Andrew D. Hurwitz (born 1947), American judge * Edward Hurwitz (born 1931), American diplomat *Emanuel Hurwitz (1919–2006), British violinist *Gregg Hurwitz, American novelist *Henry Hurwitz Jr. (1918–1992), nuclear physicist * Hyman Hurwitz (1770–1844), professor of Hebrew in England *Jake Hurwitz (born 1985), American comedian, writer and actor known for '' Jake and Amir'' and CollegeHumor *Johanna Hurwitz (born 1937), American children's author, known for books such as ''Baseball Fever'' and ''Class Clown'' *Jon Hurwitz (born 1977), A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jonty Hurwitz
Jonty Hurwitz (born 2 September 1969 in Johannesburg) is a British South African artist, engineer and entrepreneur. Hurwitz creates scientifically inspired artworks and anamorphic sculptures. He is recognised for the smallest human form ever created using nano technology. Early life Jonty Hurwitz was born in Johannesburg, South Africa, to Selwin, a hotelier and entrepreneur and Marcia Berger, a drama lecturer and teacher. Jonty and his sister (Tamara) spent their early life living in small hotels in rural towns in South Africa while his father built up his business. Jonty studied Electrical Engineering at the University of the Witwatersrand in Johannesburg from 1989 to 1993. His major was Signal Processing. He then joined the University of Cape Town Remote Sensing Group as a full-time researcher under Professor Michael Inggs, publishing a paper on radar pattern recognition. Following his research post, Hurwitz traveled for a long period of time in India studying Yog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adolf Hurwitz
Adolf Hurwitz (; 26 March 1859 – 18 November 1919) was a German mathematician who worked on algebra, analysis, geometry and number theory. Early life He was born in Hildesheim, then part of the Kingdom of Hanover, to a Jewish family and died in Zürich, in Switzerland. His father Salomon Hurwitz, a merchant, was not wealthy. Hurwitz's mother, Elise Wertheimer, died when he was three years old. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed except for an older brother, Julius, with whom he developed an arithmetical theory for complex continued fractions circa 1890. Hurwitz entered the in Hildesheim in 1868. He was taught mathematics there by Hermann Schubert. Schubert persuaded Hurwitz's father to allow him to attend university, and arranged for Hurwitz to study with Felix Klein at Munich. Salomon Hurwitz could not afford to send his son to university, but his friend, Mr. Edwards, assisted financially. Educational career Hu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hurwitz's Automorphisms Theorem
In mathematics, Hurwitz's automorphisms theorem bounds the order of the group of automorphisms, via orientation-preserving conformal mappings, of a compact Riemann surface of genus ''g'' > 1, stating that the number of such automorphisms cannot exceed 84(''g'' − 1). A group for which the maximum is achieved is called a Hurwitz group, and the corresponding Riemann surface a Hurwitz surface. Because compact Riemann surfaces are synonymous with non-singular complex projective algebraic curves, a Hurwitz surface can also be called a Hurwitz curve.Technically speaking, there is an equivalence of categories between the category of compact Riemann surfaces with the orientation-preserving conformal maps and the category of non-singular complex projective algebraic curves with the algebraic morphisms. The theorem is named after Adolf Hurwitz, who proved it in . Hurwitz's bound also holds for algebraic curves over a field of characteristic 0, and over fields of pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hurwitz Zeta Function
In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables with and by :\zeta(s,a) = \sum_^\infty \frac. This series is absolutely convergent for the given values of and and can be extended to a meromorphic function defined for all . The Riemann zeta function is . The Hurwitz zeta function is named after Adolf Hurwitz, who introduced it in 1882. Integral representation The Hurwitz zeta function has an integral representation :\zeta(s,a) = \frac \int_0^\infty \frac dx for \operatorname(s)>1 and \operatorname(a)>0. (This integral can be viewed as a Mellin transform.) The formula can be obtained, roughly, by writing :\zeta(s,a)\Gamma(s) = \sum_^\infty \frac \int_0^\infty x^s e^ \frac = \sum_^\infty \int_0^\infty y^s e^ \frac and then interchanging the sum and integral. The integral representation above can be converted to a contour integral representation :\zeta(s,a) = -\Gamma(1-s)\frac \int_C \frac dz w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jake Hurwitz
Jacob Penn Cooper Hurwitz (born August 5, 1985) is an American comedian, writer, actor, and member of the comedy duo Jake and Amir. He was hired by the comedy website CollegeHumor after becoming an intern there in 2006, and has written and appeared in original videos for the website, as well as contributing articles which have been published both online and in print. He also starred in ''The CollegeHumor Show'', an MTV sitcom that ran for one season in 2009. Outside of CollegeHumor, Hurwitz has hosted Myspace's ''BFF'' series. He is best known as the comedy partner of Amir Blumenfeld: the two appear as humorous and exaggerated versions of themselves in the web series ''Jake and Amir'', with Hurwitz generally assuming the role of the straight man. Originally made as a hobby by the pair, the series was later produced by CollegeHumor. Beginning in April 2016, they announced the streaming of their new video series, ''Lonely and Horny'', exclusively on Vimeo. The pair have also host ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mitchell Hurwitz
Mitchell Donald "Mitch" Hurwitz (born May 29, 1963) is an American television writer, producer, and actor. He is best known as the creator of the television sitcom '' Arrested Development'' as well as the co-creator of ''The Ellen Show''. He is also a contributor to '' The John Larroquette Show'' and ''The Golden Girls''. Early life Hurwitz was born in 1963 to a Jewish family in Anaheim, California. In 1976, when Hurwitz was 12, he co-founded a chocolate-chip cookie business, called the Chipyard on Balboa Boulevard in Balboa Fun Zone in Newport Beach, California, in a former taco place, with his older brother, Michael, and his father, Mark. The Chipyard is still in operation in Boston. He graduated from Estancia High School in Costa Mesa, California, and from Georgetown University in 1985 with a double major in English and theology. Early career Hurwitz worked on several sitcoms in the 1980s and 1990s, including '' Nurses'', ''The Golden Girls'', '' The Golden Palace'', '' T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
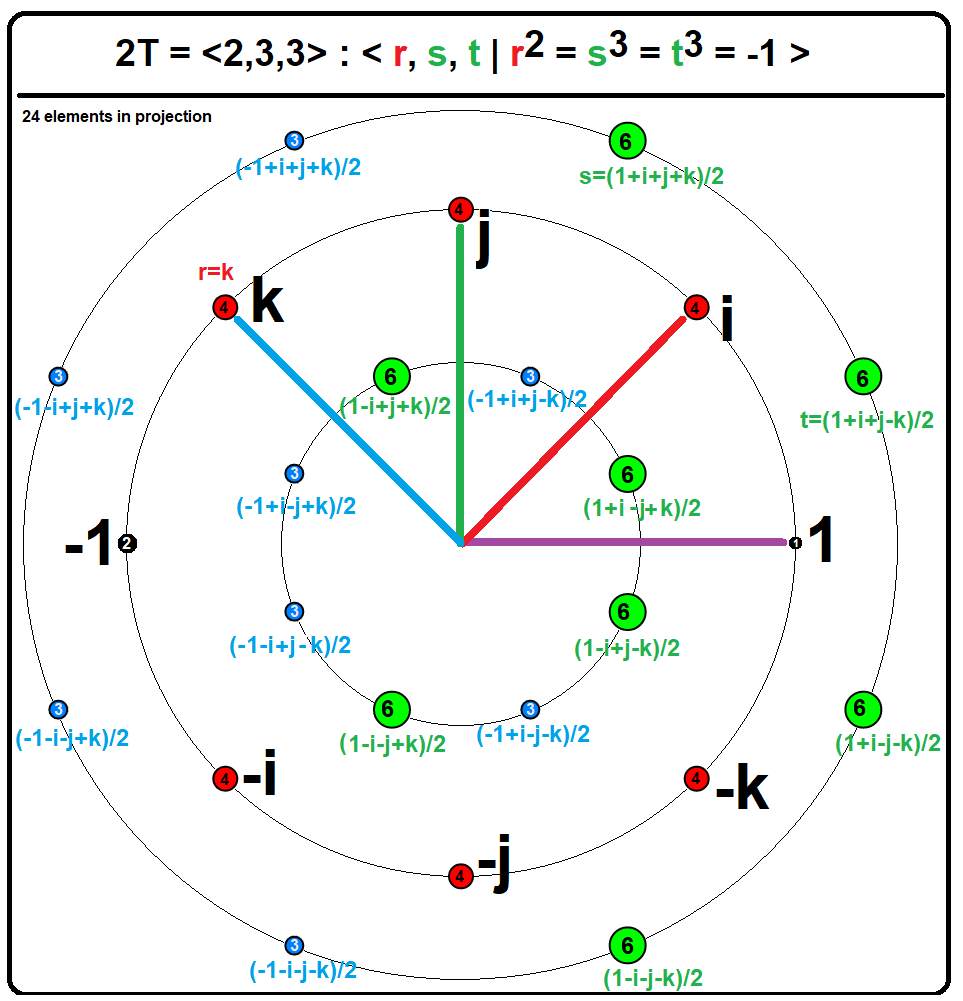
Hurwitz Quaternion
In mathematics, a Hurwitz quaternion (or Hurwitz integer) is a quaternion whose components are ''either'' all integers ''or'' all half-integers (halves of odd integers; a mixture of integers and half-integers is excluded). The set of all Hurwitz quaternions is :H = \left\. That is, either ''a'', ''b'', ''c'', ''d'' are all integers, or they are all half-integers. ''H'' is closed under quaternion multiplication and addition, which makes it a subring of the ring of all quaternions H. Hurwitz quaternions were introduced by . A Lipschitz quaternion (or Lipschitz integer) is a quaternion whose components are all integers. The set of all Lipschitz quaternions :L = \left\ forms a subring of the Hurwitz quaternions ''H''. Hurwitz integers have the advantage over Lipschitz integers that it is possible to perform Euclidean division on them, obtaining a small remainder. Both the Hurwitz and Lipschitz quaternions are examples of noncommutative domains which are not division rings. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leo Hurwitz
Leo Hurwitz (June 23, 1909 – January 18, 1991) was an American documentary filmmaker. Among the films he directed were '' Native Land'' (1942) and ''Verdict for Tomorrow'' (1961), the Emmy Award- and Peabody Award-winning film of the Eichmann trial. He was blacklisted during the McCarthy period for his strong left-wing political beliefs. Background Leo Hurwitz was born on June 23, 1909, in Brooklyn, New York, to Jewish Russian immigrants. He grew up in the Williamsburg section of Brooklyn. He had four sisters, including dancer Sophia Delza and psychoanalyst Marie Briehl. Hurwitz saw his first film at the age of four. Mesmerized by this medium of expression, he subsequently immersed himself in it. While in high school, he discovered the Harvard Club scholarship and decided to sit for the exam. Highly gifted and hard working, Hurwitz won the scholarship and attended Harvard University. Although he graduated ''summa cum laude'', he was not granted an international merit-b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Justin Hurwitz
Justin Gabriel Hurwitz (born January 22, 1985) is an American film composer and a television writer. He is best known for his longtime collaboration with director Damien Chazelle, scoring each of his films: '' Guy and Madeline on a Park Bench'' (2009), '' Whiplash'' (2014), '' La La Land'' (2016), '' First Man'' (2018), and '' Babylon'' (2022). For ''La La Land'', Hurwitz won two Academy Awards, Best Original Score and Best Original Song (for " City of Stars"), as well as the Golden Globe Awards for Best Original Score and Best Original Song and the BAFTA Award for Best Film Music. For ''First Man'' he won the Golden Globe Award for Best Original Score, and was nominated in the same category for ''Babylon''. Early life Hurwitz was born in California, the son of Gail (née Halabe), a professional ballet dancer turned registered nurse, and Ken Hurwitz, a writer. He is of Jewish heritage (from Russia, Poland, Damascus in Syria, and Beirut in Lebanon). His family moved to Wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hurwitz Matrix
In mathematics, a Hurwitz matrix, or Routh–Hurwitz matrix, in engineering stability matrix, is a structured real square matrix constructed with coefficients of a real polynomial. Hurwitz matrix and the Hurwitz stability criterion Namely, given a real polynomial :p(z)=a_z^n+a_z^+\cdots+a_z+a_n the n\times n square matrix : H= \begin a_1 & a_3 & a_5 & \dots & \dots & \dots & 0 & 0 & 0 \\ a_0 & a_2 & a_4 & & & & \vdots & \vdots & \vdots \\ 0 & a_1 & a_3 & & & & \vdots & \vdots & \vdots \\ \vdots & a_0 & a_2 & \ddots & & & 0 & \vdots & \vdots \\ \vdots & 0 & a_1 & & \ddots & & a_n & \vdots & \vdots \\ \vdots & \vdots & a_0 & & & \ddots & a_ & 0 & \vdots \\ \vdots & \vdots & 0 & & & & a_ & a_n & \vdots \\ \vdots & \vdots & \vdots & & & & a_ & a_ & 0 \\ 0 & 0 & 0 & \dots & \dots & \dots & a_ & a_ & a_n \end. is called Hurwitz matrix corresponding to the polynomial p. It was established by Adolf Hurwitz in 1895 that a real polynomial with a_0 > 0 is stable (that is, all its roots ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gregg Hurwitz
Gregg Andrew Hurwitz is an American novelist, screenwriter, and comic book writer. Most of his novels are in the thriller fiction genre. His script writing work includes a film adaptation of his book ''Orphan X'', a TV adaptation of Joby Warrick's '' Black Flags: The Rise of ISIS'', and a screenplay for the 2017 film '' The Book of Henry''. He also has written comic books for comic book publishers like DC Comics and Marvel Comics. Personal life and education Hurwitz grew up in the San Francisco Bay Area and graduated from Bellarmine College Preparatory in San Jose, California. While completing a bachelor of arts degree from Harvard University (1995) and a master's from Trinity College, Oxford in Shakespearean tragedy (1996), he wrote his first novel. At Harvard, he was a student of psychologist Jordan Peterson, who influenced his writing. He was the undergraduate scholar-athlete of the year at Harvard for pole vaulting and played college soccer in England, where he was a Kno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Routh–Hurwitz Stability Criterion
In control system theory, the Routh–Hurwitz stability criterion is a mathematical test that is a necessary and sufficient condition for the stability of a linear time-invariant (LTI) dynamical system or control system. A stable system is one whose output signal is bounded; the position, velocity or energy do not increase to infinity as time goes on. The Routh test is an efficient recursive algorithm that English mathematician Edward John Routh proposed in 1876 to determine whether all the roots of the characteristic polynomial of a linear system have negative real parts. German mathematician Adolf Hurwitz independently proposed in 1895 to arrange the coefficients of the polynomial into a square matrix, called the Hurwitz matrix, and showed that the polynomial is stable if and only if the sequence of determinants of its principal submatrices are all positive. The two procedures are equivalent, with the Routh test providing a more efficient way to compute the Hurwitz determin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |