|
Hold-out Cross-validation
Cross-validation, sometimes called rotation estimation or out-of-sample testing, is any of various similar model validation techniques for assessing how the results of a statistical analysis will generalize to an independent data set. Cross-validation includes resampling and sample splitting methods that use different portions of the data to test and train a model on different iterations. It is often used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. It can also be used to assess the quality of a fitted model and the stability of its parameters. In a prediction problem, a model is usually given a dataset of ''known data'' on which training is run (''training dataset''), and a dataset of ''unknown data'' (or ''first seen'' data) against which the model is tested (called the validation dataset or ''testing set''). The goal of cross-validation is to test the model's ability to predict new data t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confusion Matrix
In the field of machine learning and specifically the problem of statistical classification, a confusion matrix, also known as error matrix, is a specific table layout that allows visualization of the performance of an algorithm, typically a supervised learning one; in unsupervised learning it is usually called a matching matrix. Each row of the matrix represents the instances in an actual class while each column represents the instances in a predicted class, or vice versa – both variants are found in the literature. The diagonal of the matrix therefore represents all instances that are correctly predicted. The name stems from the fact that it makes it easy to see whether the system is confusing two classes (i.e. commonly mislabeling one as another). It is a special kind of contingency table, with two dimensions ("actual" and "predicted"), and identical sets of "classes" in both dimensions (each combination of dimension and class is a variable in the contingency table). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Model
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of Sample (statistics), sample data (and similar data from a larger Statistical population, population). A statistical model represents, often in considerably idealized form, the Data generating process, data-generating process. When referring specifically to probability, probabilities, the corresponding term is probabilistic model. All Statistical hypothesis testing, statistical hypothesis tests and all Estimator, statistical estimators are derived via statistical models. More generally, statistical models are part of the foundation of statistical inference. A statistical model is usually specified as a mathematical relationship between one or more random variables and other non-random variables. As such, a statistical model is "a formal representation of a theory" (Herman J. Adèr, Herman Adèr quoting Kenneth A. Bollen, Kenneth Bollen). Introduction Informally, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
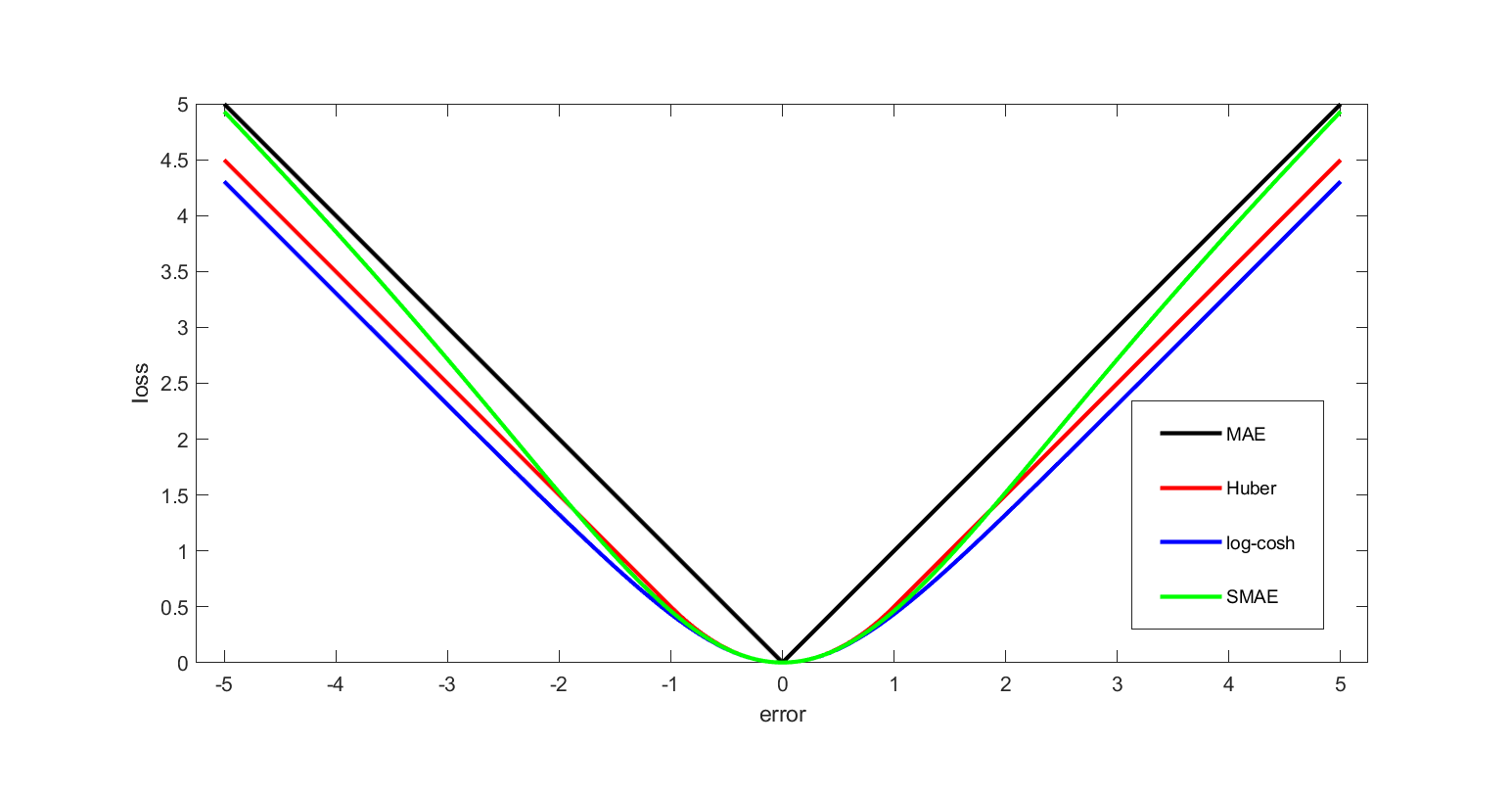
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, Mathematical finance, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the Problem solving, answer to a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, the following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be Prior probability, priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bias (statistics)
In the field of statistics, bias is a systematic tendency in which the methods used to gather data and estimate a sample statistic present an inaccurate, skewed or distorted ('' biased'') depiction of reality. Statistical bias exists in numerous stages of the data collection and analysis process, including: the source of the data, the methods used to collect the data, the estimator chosen, and the methods used to analyze the data. Data analysts can take various measures at each stage of the process to reduce the impact of statistical bias in their work. Understanding the source of statistical bias can help to assess whether the observed results are close to actuality. Issues of statistical bias has been argued to be closely linked to issues of statistical validity. Statistical bias can have significant real world implications as data is used to inform decision making across a wide variety of processes in society. Data is used to inform lawmaking, industry regulation, corp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Squared Error
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the true value. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate. In machine learning, specifically empirical risk minimization, MSE may refer to the ''empirical'' risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution). The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the erro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is one less than that of the ambient space. Two lower-dimensional examples of hyperplanes are one-dimensional lines in a plane and zero-dimensional points on a line. Most commonly, the ambient space is -dimensional Euclidean space, in which case the hyperplanes are the -dimensional "flats", each of which separates the space into two half spaces. A reflection across a hyperplane is a kind of motion ( geometric transformation preserving distance between points), and the group of all motions is generated by the reflections. A convex polytope is the intersection of half-spaces. In non-Euclidean geometry, the ambient space might be the -dimensional sphere or hyperbolic space, or more generally a pseudo-Riemannian space form, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The method is widely used in areas such as regression analysis, curve fitting and data modeling. The least squares method can be categorized into linear and nonlinear forms, depending on the relationship between the model parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. History Founding The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Euclidean vectors can be added and scaled to form a vector space. A '' vector quantity'' is a vector-valued physical quantity, including units of measurement and possibly a support, formulated as a '' directed line segment''. A vector is frequently depicted graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \stackrel \longrightarrow. A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word means 'carrier'. It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Population
In statistics, a population is a set of similar items or events which is of interest for some question or experiment. A statistical population can be a group of existing objects (e.g. the set of all stars within the Milky Way galaxy) or a hypothetical and potentially infinite group of objects conceived as a generalization from experience (e.g. the set of all possible hands in a game of poker). A population with finitely many values N in the support of the population distribution is a finite population with population size N. A population with infinitely many values in the support is called infinite population. A common aim of statistical analysis is to produce information about some chosen population. In statistical inference, a subset of the population (a statistical '' sample'') is chosen to represent the population in a statistical analysis. Moreover, the statistical sample must be unbiased and accurately model the population. The ratio of the size of this statistical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |