|
History Of Network Traffic Models
Design of robust and reliable networks and network services relies on an understanding of the traffic characteristics of the network. Throughout history, different models of network traffic have been developed and used for evaluating existing and proposed networks and services. Demands on computer networks are not entirely predictable. Performance modeling is necessary for deciding the quality of service (QoS) level. Performance models in turn, require accurate traffic models that have the ability to capture the statistical characteristics of the actual traffic on the network. Many traffic models have been developed based on traffic measurement data. If the underlying traffic models do not efficiently capture the characteristics of the actual traffic, the result may be the under-estimation or over-estimation of the performance of the network. This impairs the design of the network. Traffic models are hence, a core component of any performance evaluation of networks and they need t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NPOV
Neutral point of view may refer to: * Objectivity (science), the concept of a position formed without incorporating one's own prejudice * Neutrality (philosophy), to maintain neutrality at all times {{Disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Brownian Motion
In probability theory, fractional Brownian motion (fBm), also called a fractal Brownian motion, is a generalization of Brownian motion. Unlike classical Brownian motion, the increments of fBm need not be independent. fBm is a continuous-time Gaussian process ''BH''(''t'') on , ''T'' that starts at zero, has expectation zero for all ''t'' in , ''T'' and has the following covariance function: :E_H(t) B_H (s)\tfrac (, t, ^+, s, ^-, t-s, ^), where ''H'' is a real number in (0, 1), called the Hurst index or Hurst parameter associated with the fractional Brownian motion. The Hurst exponent describes the raggedness of the resultant motion, with a higher value leading to a smoother motion. It was introduced by . The value of ''H'' determines what kind of process the ''fBm'' is: * if ''H'' = 1/2 then the process is in fact a Brownian motion or Wiener process; * if ''H'' > 1/2 then the increments of the process are positively correlated; * if ''H'' < 1/2 then the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Traffic Generation Model
A traffic generation model is a stochastic model of the traffic flows or data sources in a communication network, for example a cellular network or a computer network. A packet generation model is a traffic generation model of the packet flows or data sources in a packet-switched network. For example, a web traffic model is a model of the data that is sent or received by a user's web-browser. These models are useful during the development of telecommunication technologies, in view to analyse the performance and capacity of various protocols, algorithms and network topologies . Application The network performance can be analyzed by network traffic measurement in a testbed network, using a network traffic generator such as iperf, bwping and Mausezahn. The traffic generator sends dummy packets, often with a unique packet identifier, making it possible to keep track of the packet delivery in the network. Numerical analysis using network simulation is often a less expensive appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long Tail
In statistics and business, a long tail of some distributions of numbers is the portion of the distribution having many occurrences far from the "head" or central part of the distribution. The distribution could involve popularities, random numbers of occurrences of events with various probabilities, etc. The term is often used loosely, with no definition or an arbitrary definition, but precise definitions are possible. In statistics, the term ''long-tailed distribution'' has a narrow technical meaning, and is a subtype of heavy-tailed distribution. Intuitively, a distribution is (right) long-tailed if, for any fixed amount, when a quantity exceeds a high level, it almost certainly exceeds it by at least that amount: large quantities are probably even larger. Note that there is no sense of ''the'' "long tail" of a distribution, but only the ''property'' of a distribution being long-tailed. In business, the term ''long tail'' is applied to rank-size distributions or rank-f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ns (simulator)
ns (from network simulator) is a name for a series of discrete event network simulators, specifically ns-1, ns-2, and ns-3. All are discrete-event computer network simulators, primarily used in research and teaching. History ns-1 The first version of ns, known as ns-1, was developed at Lawrence Berkeley National Laboratory (LBNL) in the 1995-97 timeframe by Steve McCanne, Sally Floyd, Kevin Fall, and other contributors. This was known as the LBNL Network Simulator, and derived in 1989 from an earlier simulator known as REAL by S. Keshav. ns-2 Ns-2 began as a revision of ns-1. From 1997 to 2000, ns development was supported by DARPA through the VINT project at LBL, Xerox PARC, UCB, and USC/ISI. In 2000, ns-2 development was supported through DARPA with SAMAN and through NSF with CONSER, both at USC/ISI, in collaboration with other researchers including ACIRI. Features of NS2 1. It is a discrete event simulator for networking research. 2. It provides substantial s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Packet Train
Packet may refer to: * A small container or pouch ** Packet (container), a small single use container ** Cigarette packet ** Sugar packet * Network packet, a formatted unit of data carried by a packet-mode computer network * Packet radio, a form of amateur radio data communications using the AX25 protocol * Packet trade, regularly scheduled cargo, passenger, and mail trade conducted by ship * Packet boat, type of boat used for scheduled mail or passenger service * C-82 Packet, a U.S. military transport aircraft * ''Packet Newspapers'', British newspaper group See also * * * Package (other) * Pack (other) * Kit (other) * MacGuffin - A plot device in the form of some goal, desired object, or another motivator popularized in the 1930s by Alfred Hitchcock Sir Alfred Joseph Hitchcock (13 August 1899 – 29 April 1980) was an English filmmaker. He is widely regarded as one of the most influential figures in the history of cinema. In a career sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Model
In probability theory, a Markov model is a stochastic model used to model pseudo-randomly changing systems. It is assumed that future states depend only on the current state, not on the events that occurred before it (that is, it assumes the Markov property). Generally, this assumption enables reasoning and computation with the model that would otherwise be intractable. For this reason, in the fields of predictive modelling and probabilistic forecasting, it is desirable for a given model to exhibit the Markov property. Introduction There are four common Markov models used in different situations, depending on whether every sequential state is observable or not, and whether the system is to be adjusted on the basis of observations made: Markov chain The simplest Markov model is the Markov chain. It models the state of a system with a random variable that changes through time. In this context, the Markov property suggests that the distribution for this variable depends only ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Poisson Process
A compound Poisson process is a continuous-time (random) stochastic process with jumps. The jumps arrive randomly according to a Poisson process and the size of the jumps is also random, with a specified probability distribution. A compound Poisson process, parameterised by a rate \lambda > 0 and jump size distribution ''G'', is a process \ given by :Y(t) = \sum_^ D_i where, \ is a counting of a Poisson process with rate \lambda, and \ are independent and identically distributed random variables, with distribution function ''G'', which are also independent of \.\, When D_i are non-negative integer-valued random variables, then this compound Poisson process is known as a stuttering Poisson process which has the feature that two or more events occur in a very short time. Properties of the compound Poisson process The expected value of a compound Poisson process can be calculated using a result known as Wald's equation as: :\operatorname E(Y(t)) = \operatorname E(D_1 + \cdo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. It is named after French mathematician Siméon Denis Poisson (; ). The Poisson distribution can also be used for the number of events in other specified interval types such as distance, area, or volume. For instance, a call center receives an average of 180 calls per hour, 24 hours a day. The calls are independent; receiving one does not change the probability of when the next one will arrive. The number of calls received during any minute has a Poisson probability distribution with mean 3: the most likely numbers are 2 and 3 but 1 and 4 are also likely and there is a small probability of it being as low as zero and a very small probability it could be 10. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
TES Model
Tes or TES may refer to: Places * Tés, a village in Hungary * Tes River, a river in Mongolia * Tes, Uvs, a district in Mongolia's Uvs Province * Tes, Zavkhan, a district in Mongolia's Zavkhan Province * Teş, a village in Brestovăț Commune, Timiș County, Romania Arts and entertainment * Teatrul Evreiesc de Stat, the State Jewish Theater in Romania * ''The Early Show'', a morning television program on CBS in the United States * ''The Elder Scrolls'', a video game series by Bethesda Softworks * ''The Eminem Show'', a 2002 album by hip-hop artist Eminem * Tes (rapper), American rapper from Brooklyn, New York, US Science and technology * Thermal energy storage, a group of technologies which are used to store and release thermal energy * Transition edge sensor, a type of superconducting detector used in physics and astronomy * Bellanca TES, an experimental aircraft constructed by Giuseppe Mario Bellanca in 1929 Biology and chemistry * TES (buffer), a common buffer solution in bi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
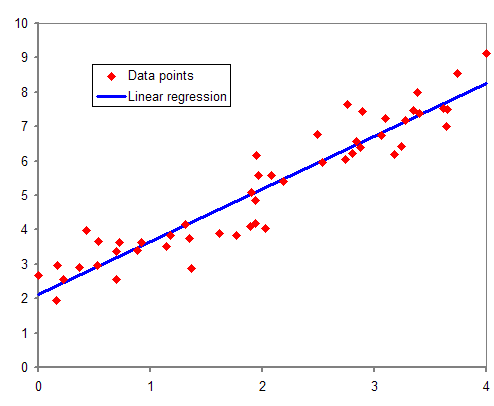
Regression Model
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given set o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autoregressive Model
In statistics, econometrics and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it is used to describe certain time-varying processes in nature, economics, etc. The autoregressive model specifies that the output variable depends linearly on its own previous values and on a stochastic term (an imperfectly predictable term); thus the model is in the form of a stochastic difference equation (or recurrence relation which should not be confused with differential equation). Together with the moving-average (MA) model, it is a special case and key component of the more general autoregressive–moving-average (ARMA) and autoregressive integrated moving average (ARIMA) models of time series, which have a more complicated stochastic structure; it is also a special case of the vector autoregressive model (VAR), which consists of a system of more than one interlocking stochastic difference equation in more than one evolving random vari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |