|
Higher Order Sinusoidal Input Describing Function
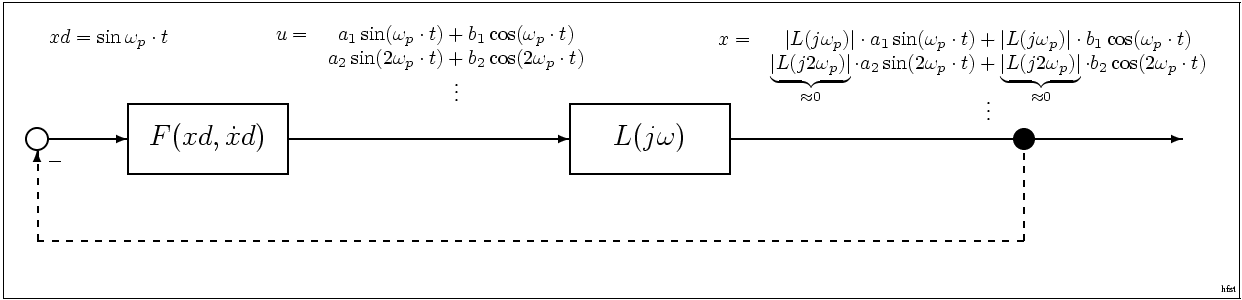
Definition The higher-order sinusoidal input describing functions (HOSIDF) were first introduced bdr. ir. P.W.J.M. Nuij The HOSIDFs are an extension of the sinusoidal input describing functionGelb, A., and W. E. Vander Velde: Multiple-Input Describing Functions and Nonlinear System Design, McGraw Hill, 1968. which describe the response (gain and phase) of a system at harmonics of the base frequency of a sinusoidal input signal. The HOSIDFs bear an intuitive resemblance to the classical frequency response function and define the periodic output of a stable, causal, time invariant nonlinear system to a sinusoidal A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the '' sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in ... input signal: u(t) = \gamma \sin(\omega_0 t + \varphi_0) This output is denoted by y(t) and consists of harmonics of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Describing Function
In control systems theory, the describing function (DF) method, developed by Nikolay Mitrofanovich Krylov and Nikolay Bogoliubov in the 1930s, and extended by Ralph Kochenburger is an approximate procedure for analyzing certain nonlinear control problems. It is based on quasi-linearization, which is the approximation of the non-linear system under investigation by a linear time-invariant (LTI) transfer function that depends on the amplitude of the input waveform. By definition, a transfer function of a true LTI system cannot depend on the amplitude of the input function because an LTI system is linear. Thus, this dependence on amplitude generates a family of linear systems that are combined in an attempt to capture salient features of the non-linear system behavior. The describing function is one of the few widely applicable methods for designing nonlinear systems, and is very widely used as a standard mathematical tool for analyzing limit cycles in closed-loop controller ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gain (electronics)
In electronics, gain is a measure of the ability of a two-port circuit (often an amplifier) to increase the power or amplitude of a signal from the input to the output port by adding energy converted from some power supply to the signal. It is usually defined as the mean ratio of the signal amplitude or power at the output port to the amplitude or power at the input port. It is often expressed using the logarithmic decibel (dB) units ("dB gain"). A gain greater than one (greater than zero dB), that is amplification, is the defining property of an active component or circuit, while a passive circuit will have a gain of less than one. The term ''gain'' alone is ambiguous, and can refer to the ratio of output to input voltage (''voltage gain''), current (''current gain'') or electric power (''power gain''). In the field of audio and general purpose amplifiers, especially operational amplifiers, the term usually refers to voltage gain, but in radio frequency amplifiers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
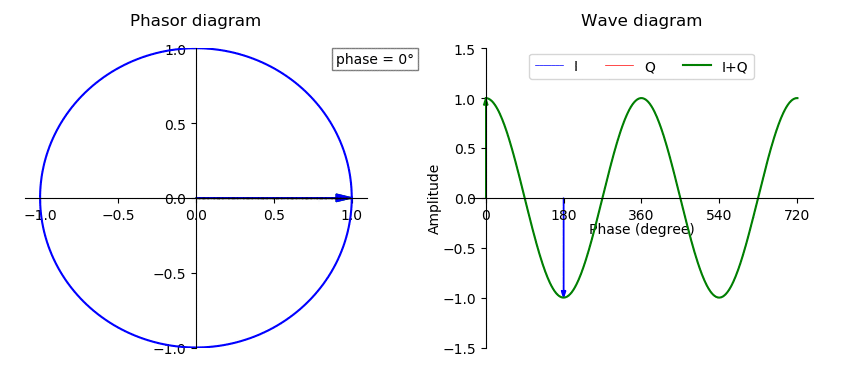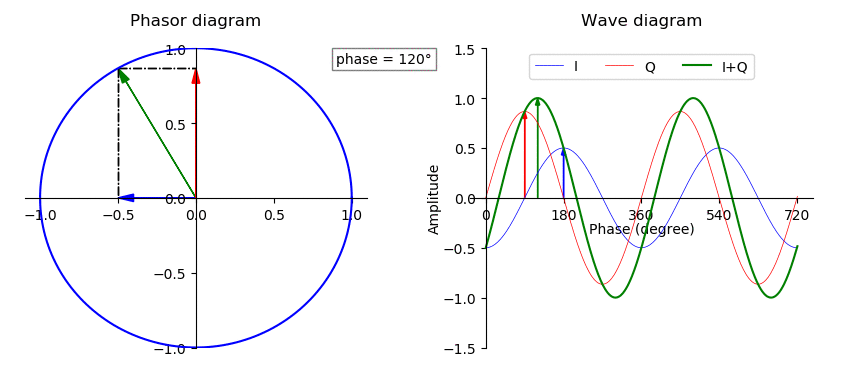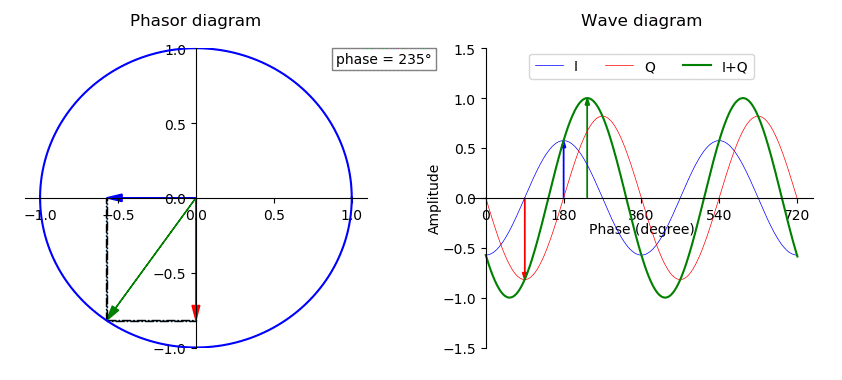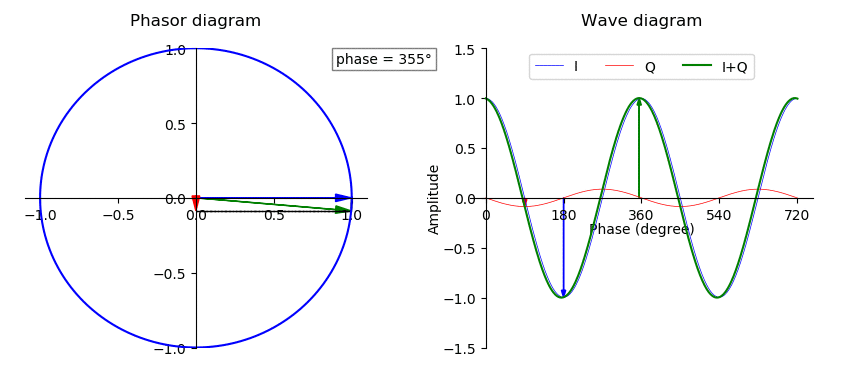
Phase (waves)
In physics and mathematics, the phase of a periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is denoted \phi(t) and expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \phi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \phi(t) is also a periodic function, with the same period as F, that repeatedly scans the same range ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Response Function
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of systems, such as audio and control systems, where they simplify mathematical analysis by converting governing differential equations into algebraic equations. In an audio system, it may be used to minimize audible distortion by designing components (such as microphones, amplifiers and loudspeakers) so that the overall response is as flat (uniform) as possible across the system's bandwidth. In control systems, such as a vehicle's cruise control, it may be used to assess system stability, often through the use of Bode plots. Systems with a specific frequency response can be designed using analog and digital filters. The frequency response characterizes systems in the frequency domain, just as the impulse response characterizes systems in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Causal System
In control theory, a causal system (also known as a physical or nonanticipative system) is a system where the output depends on past and current inputs but not future inputs—i.e., the output y(t_) depends only on the input x(t) for values of t \le t_. The idea that the output of a function at any time depends only on past and present values of input is defined by the property commonly referred to as causality. A system that has ''some'' dependence on input values from the future (in addition to possible dependence on past or current input values) is termed a non-causal or acausal system, and a system that depends ''solely'' on future input values is an anticausal system. Note that some authors have defined an anticausal system as one that depends solely on future ''and present'' input values or, more simply, as a system that does not depend on past input values. Classically, nature or physical reality has been considered to be a causal system. Physics involving special rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Invariant
In control theory, a time-invariant (TIV) system has a time-dependent system function that is not a direct function of time. Such systems are regarded as a class of systems in the field of system analysis. The time-dependent system function is a function of the time-dependent input function. If this function depends ''only'' indirectly on the time-domain (via the input function, for example), then that is a system that would be considered time-invariant. Conversely, any direct dependence on the time-domain of the system function could be considered as a "time-varying system". Mathematically speaking, "time-invariance" of a system is the following property: :''Given a system with a time-dependent output function , and a time-dependent input function , the system will be considered time-invariant if a time-delay on the input directly equates to a time-delay of the output function. For example, if time is "elapsed time", then "time-invariance" implies that the relationship be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear System
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems. Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Wave
A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the '' sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in mathematics, as well as in physics, engineering, signal processing and many other fields. Formulation Its most basic form as a function of time (''t'') is: y(t) = A\sin(2 \pi f t + \varphi) = A\sin(\omega t + \varphi) where: * ''A'', ''amplitude'', the peak deviation of the function from zero. * ''f'', '' ordinary frequency'', the ''number'' of oscillations (cycles) that occur each second of time. * ''ω'' = 2''f'', '' angular frequency'', the rate of change of the function argument in units of radians per second. * \varphi, '' phase'', specifies (in radians) where in its cycle the oscillation is at ''t'' = 0. When \varphi is non-zero, the entire waveform appears to be shifted in time by the amount ''φ''/''ω'' seconds. A negative val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems which use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the latter half of the 19th century after commercialization of the electric telegraph, the telephone, and electrical power generation, distribution, and use. Electrical engineering is now divided into a wide range of different fields, including computer engineering, systems engineering, power engineering, telecommunications, radio-frequency engineering, signal processing, instrumentation, photovoltaic cells, electronics, and optics and photonics. Many of these disciplines overlap with other engineering branches, spanning a huge number of specializations including hardware engineering, power electronics, electromagnetics and waves, microwave engineering, nanotechnology, electrochemistry, renewable energies, mechatronics/control, and electrical m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control stability; often with the aim to achieve a degree of optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects which are also studied are controllability and observability. Control theory is used in control sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |