|
Helmholtz Decomposition
In physics and mathematics, the Helmholtz decomposition theorem or the fundamental theorem of vector calculus states that certain differentiable vector fields can be resolved into the sum of an irrotational ( curl-free) vector field and a solenoidal (divergence-free) vector field. In physics, often only the decomposition of sufficiently smooth, rapidly decaying vector fields in three dimensions is discussed. It is named after Hermann von Helmholtz. Definition For a vector field \mathbf \in C^1(V, \mathbb^n) defined on a domain V \subseteq \mathbb^n, a Helmholtz decomposition is a pair of vector fields \mathbf \in C^1(V, \mathbb^n) and \mathbf \in C^1(V, \mathbb^n) such that: \begin \mathbf(\mathbf) &= \mathbf(\mathbf) + \mathbf(\mathbf), \\ \mathbf(\mathbf) &= - \nabla \Phi(\mathbf), \\ \nabla \cdot \mathbf(\mathbf) &= 0. \end Here, \Phi \in C^2(V, \mathbb) is a scalar potential, \nabla \Phi is its gradient, and \nabla \cdot \mathbf is the divergence of the vector fiel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as classical antiquity, antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Nikolai Lobachevsky, Lobachevsky. The simplest examples of smooth spaces are the Differential geometry of curves, plane and space curves and Differential geometry of surfaces, surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergence Theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem relating the '' flux'' of a vector field through a closed surface to the ''divergence'' of the field in the volume enclosed. More precisely, the divergence theorem states that the surface integral of a vector field over a closed surface, which is called the "flux" through the surface, is equal to the volume integral of the divergence over the region enclosed by the surface. Intuitively, it states that "the sum of all sources of the field in a region (with sinks regarded as negative sources) gives the net flux out of the region". The divergence theorem is an important result for the mathematics of physics and engineering, particularly in electrostatics and fluid dynamics. In these fields, it is usually applied in three dimensions. However, it generalizes to any number of dimensions. In one dimension, it is equivalent to the fundamental theorem of cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Laplacian
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is the nabla operator), or \Delta. In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian of a function at a point measures by how much the average value of over small spheres or balls centered at deviates from . The Laplace operator is named after the French mathematician Pierre-Simon de Laplace (1749–1827), who first applied the operator to the study of celestial mechanics: the Laplacian of the gravitational potential due to a given mass density distribution is a constant multiple of that density ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplacian
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is the nabla operator), or \Delta. In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian of a function at a point measures by how much the average value of over small spheres or balls centered at deviates from . The Laplace operator is named after the French mathematician Pierre-Simon de Laplace (1749–1827), who first applied the operator to the study of celestial mechanics: the Laplacian of the gravitational potential due to a given mass density distribution is a constant multiple of that de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Delta Function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be represented heuristically as \delta (x) = \begin 0, & x \neq 0 \\ , & x = 0 \end such that \int_^ \delta(x) dx=1. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limits or, as is common in mathematics, measure theory and the theory of distributions. The delta function was introduced by physicist Paul Dirac, and has since been applied routinely in physics and engineering to model point masses and instantaneous impulses. It is called the delta function because it is a continuous analogue of the Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1. The mathematical rigor of the delta function wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nabla Operator
Del, or nabla, is an operator used in mathematics (particularly in vector calculus) as a vector differential operator, usually represented by the nabla symbol ∇. When applied to a function defined on a one-dimensional domain, it denotes the standard derivative of the function as defined in calculus. When applied to a ''field'' (a function defined on a multi-dimensional domain), it may denote any one of three operations depending on the way it is applied: the gradient or (locally) steepest slope of a scalar field (or sometimes of a vector field, as in the Navier–Stokes equations); the divergence of a vector field; or the curl (rotation) of a vector field. Del is a very convenient mathematical notation for those three operations (gradient, divergence, and curl) that makes many equations easier to write and remember. The del symbol (or nabla) can be formally defined as a vector operator whose components are the corresponding partial derivative operators. As a ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a ''scalar potential'', which is a scalar field whose gradient is a given vector field. Formally, given a vector field \mathbf, a ''vector potential'' is a C^2 vector field \mathbf such that \mathbf = \nabla \times \mathbf. Consequence If a vector field \mathbf admits a vector potential \mathbf, then from the equality \nabla \cdot (\nabla \times \mathbf) = 0 (divergence of the curl is zero) one obtains \nabla \cdot \mathbf = \nabla \cdot (\nabla \times \mathbf) = 0, which implies that \mathbf must be a solenoidal vector field. Theorem Let \mathbf : \R^3 \to \R^3 be a solenoidal vector field which is twice continuously differentiable. Assume that \mathbf(\mathbf) decreases at least as fast as 1/\, \mathbf\, for \, \mathbf\, \to \infty . Define \mathbf (\mathbf) = \frac \int_ \frac \, d^3\mathbf where \nabla_y \times denotes curl with respect to variab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounded Domain
In mathematical analysis, a domain or region is a non-empty, connected, and open set in a topological space. In particular, it is any non-empty connected open subset of the real coordinate space or the complex coordinate space . A connected open subset of coordinate space is frequently used for the domain of a function. The basic idea of a connected subset of a space dates from the 19th century, but precise definitions vary slightly from generation to generation, author to author, and edition to edition, as concepts developed and terms were translated between German, French, and English works. In English, some authors use the term ''domain'', some use the term ''region'', some use both terms interchangeably, and some define the two terms slightly differently; some avoid ambiguity by sticking with a phrase such as ''non-empty connected open subset''. Conventions One common convention is to define a ''domain'' as a connected open set but a ''region'' as the union (set theory), uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bump Function
In mathematical analysis, a bump function (also called a test function) is a function f : \Reals^n \to \Reals on a Euclidean space \Reals^n which is both smooth (in the sense of having continuous derivatives of all orders) and compactly supported. The set of all bump functions with domain \Reals^n forms a vector space, denoted \mathrm^\infty_0(\Reals^n) or \mathrm^\infty_\mathrm(\Reals^n). The dual space of this space endowed with a suitable topology is the space of distributions. Examples The function \Psi : \mathbb \to \mathbb given by \Psi(x) = \begin \exp\left( \frac\right), & \text , x, . In fact, by definition of support, we have that \operatorname(\Psi):=\overline =\overline, where the closure is taken with respect the Euclidean topology of the real line. The proof of smoothness follows along the same lines as for the related function discussed in the Non-analytic smooth function article. This function can be interpreted as the Gaussian function \exp\le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robotics
Robotics is the interdisciplinary study and practice of the design, construction, operation, and use of robots. Within mechanical engineering, robotics is the design and construction of the physical structures of robots, while in computer science, robotics focuses on robotic automation algorithms. Other disciplines contributing to robotics include electrical engineering, electrical, control engineering, control, software engineering, software, Information engineering (field), information, electronics, electronic, telecommunications engineering, telecommunication, computer engineering, computer, mechatronic, and materials engineering, materials engineering. The goal of most robotics is to design machines that can help and assist humans. Many robots are built to do jobs that are hazardous to people, such as finding survivors in unstable ruins, and exploring space, mines and shipwrecks. Others replace people in jobs that are boring, repetitive, or unpleasant, such as cleaning, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
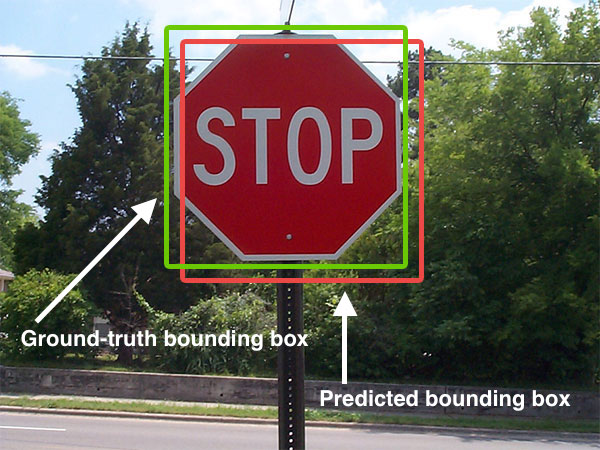
Computer Vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the form of decisions. "Understanding" in this context signifies the transformation of visual images (the input to the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scientific discipline of computer vision is concerned with the theory behind artificial systems that extract information from images. Image data can take many forms, such as video sequences, views from multiple cameras, multi-dimensional data from a 3D scanning, 3D scanner, 3D point clouds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |